2. Математическое описание химических реакций

Статика и динамика реагирующих химических систем (состав (состояние), равновесие, кинетика). Стехиометрия как описание состава (не структуры).

Стехиоме́трия— система законов, правил и терминов, обосновывающих расчёты состава веществ и количественных соотношений между массами (объёмами для газов) веществ в химических реакциях.

Химическая формула как объект алгебры. Реагент, продукт, интермедиат – реактант, вещество. Уравнения реакции (стадии) как объекты алгебры. Линейная зависимость стадий в задачах химии.

С + О2 = СО2 , (3.1)

С + СО2 = 2СО, (3.2)

2С + О2 = 2СО. (3.3)

Стадия (3.3) может быть представлена как сумма (3.1) и (3.2): если мы формально сложим первое уравнение со вторым и приведем подобные, т.е. взаимно уничтожим символы СО2 в левой и правой частях, то получим уравнение (3.3). То есть, третья строка является линейной комбинацией первых двух (сумма – простейший, хотя не единственный, случай линейных комбинаций).

Стехиометрическое уравнение реакции имеет ясный количественный смысл. Поэтому обращение с формулами веществ как с величинами корректно. Это важное свойство стехиометрических уравнений назовем алгебраичностью.

Линейная зависимость или независимость ничего не говорит о реальном механизме реакции. В одних случаях линейно независимая схема отвечает действительному ходу процесса, в других – процесс содержит и линейно зависимые стадии.

Линейная независимость стадий важна при решении задач химического равновесия в сложных (многостадийных) реакциях. Здесь линейно независимой системе стадий соответствует достаточный для описания и расчета набор констант равновесия. А для любой линейно зависимой стадии константа может быть получена как функция констант этого набора. Например, для реакций (3.1) – (3.3) имеем К3 = К1 · К2 .

Механизм как частный случай стехиометрии.

Стехиометрическая матрица (однородные уравнения).

Нумерация: m реакций, n реактантов.

АхФ=У. Ранг А и число ЛН стадий и реактантов.

Вернемся к реакциям (3.1) – (3.3). Сейчас каждое из этих уравнений рассматривается как стадия единой сложной реакции. В соответствии с алгебраичностью уравнений мы вправе перенести все члены уравнений в одну сторону:

– С – О2 + СО2 = 0,

– С – СО2 + 2СО = 0, (3.4)

– 2С – О2 + 2СО =0.

В системе (3.4) знаки выбраны так: если какое-то вещество J на данной стадии расходуется, его стехиометрический коэффициент aJ < 0; если J образуется, aJ > 0; если J не участвует в стехиометрии данной стадии, то aJ = 0. Это правило знаков будем широко использовать в дальнейшем изложении. Система уравнений (3.4) – это система однородных уравнений 1-й степени (однородные уравнения – такие, у которых свободные члены равны нулю). Такая система может быть полностью охарактеризована матрицей коэффициентов:

Здесь n – общее число веществ; m – число стадий реакции; aij – стехиометрический коэффициент j-го вещества в i-й стадии с учетом правила знаков. Матрицу a называют стехиометрической.

Матрица размера m × n – прямоугольная таблица (m строк и n столбцов), составленная из чисел или алгебраических выражений aij, называемых элементами матрицы. Квадратная матрица n × n – это матрица, в которой число строк равно числу столбцов. Для нее число n называют порядком матрицы. Подматрица матрицы – это такая матрица, которая получается из данной путем вычеркивания любого числа столбцов и любого числа строк. Определитель (детерминант) квадратной матрицы, элементы которой числа, – это число, получаемое из элементов по определенному правилу, которое здесь не приводится из-за громоздкости. Если определитель равен нулю, то матрицу называют вырожденной (особенной), если не равен, – то невырожденной (неособенной).

Ранг матрицы. Рассмотрим все возможные квадратные подматрицы порядка l некоторой матрицы а размера m × n (рассматриваются любые целые положительные l, удовлетворяющие условию l ≤ m и l ≤ n). Некоторые из этих подматриц окажутся вырожденными, другие – невырожденными. Найдем наибольший порядок l макс, для которого существует хотя бы одна невырожденная подматрица. Этот порядок называют рангом матрицы а и обозначают r g a:

r g a=l макс. (3.7)

Ранг матрицы и число линейно независимых строк (столбцов). Если m ≤n и r g a =m, то все m строк матрицы линейно независимы. Если r g a < m, то среди строк имеется (m – r g a) линейно зависимых. Точно так же если n ≤m и r g a =n, то линейно независимы все столбцы, а если r g a < n, то в матрице имеются линейно зависимые столбцы. В частности, отсюда следует, что для того, чтобы система реакций была линейно независимой, необходимо, чтобы число строк (стадий) не превышало числа столбцов (веществ). Более подробное рассмотрение показывает, что необходимое условие линейной независимости стадий еще жестче: m < n. (3.8)

В линейно независимой системе число реакций всегда меньше числа веществ, участвующих в ней как исходные (реагенты) и как продукты.

Атомная матрица Н: n реактантов, l атомов (квазиатомов).

Ф=НхЗ. Стехиометрическое правило Гиббса RkA  n-RkH.

Удобным инструментом при анализе стехиометрии является атомная матрица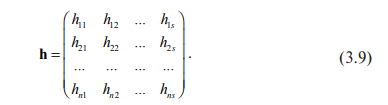

Строки этой матрицы соответствуют веществам, участвующим в реакции, а столбцы – атомам, из которых состоят эти вещества. Элемент hpq матрицы – количество атомов данного сорта q в молекуле (или формульной единице) вещества Ap ; n – общее число веществ; s – количество сортов атомов, составляющих эти вещества. Так, для реакции (3.1) – (3.3), если пронумеровать вещества в порядке С, О2 , СО, СО2 , а атомы в порядке С, О, то

Важная особенность атомных матриц – возможность в ряде случаев вводить в нее в качестве столбцов квазиатомы. Если какая-либо группа атомов переходит из одних веществ в другие, нигде не изменяясь количественно, то такая группа может рассматриваться как «атом», точнее квазиатом.

Преобразованием стехиометрической и атомной матриц можно получить правило Гиббса: r g a ≤n – r g h,

где n – число веществ–участников реакции. Здесь знак «<» может быть только в том маловероятном случае, когда в записи системы уравнений пропущена какая-то линейно независимая стадия. В обычном случае правило Гиббса – это равенство:

r g a=n – r g h. (3.17)

Например, для реакций (3.1) – (3.3) n = 4, ранг матрицы (3.10) равен 2; значит, r g a= 4 – 2 = 2 и две из стадий реакции линейно независимы. Для реакций (3.11) n= 6, r g h= 3; отсюда r g a= 6 – 3 =3 и все три стадии линейно независимы. Можно сформулировать два правила, позволяющих в неслишком трудных случаях находить линейно независимые стадии сложных реакций, не прибегая к формальному анализу. Процедура заключается в последовательном вычеркивании независимых стадий.

Правило 1. Если стехиометрический коэффициент какого-то вещества отличен от нуля только в одной из стадий, эта стадия независима и ее можно вычеркнуть.

Правило 2. После такого вычеркивания для оставшихся стадий продолжает действовать правило 1. Вычеркивание продолжается либо до тех пор, пока не останется лишь одна стадия (она, разумеется, будет независима), либо пока для немногих оставшихся стадий не удастся установить линейную зависимость.

Простая и сложная реакция.

Химическая переменная =g_i/a_i – обозначение глубины протекания стадии (знак плюс по продукту).

Рассмотрим формально одностадийную реакцию: а1 А1 + а2 А2 + … +аn Аn = 0. (3.18) Формально простой (формально одностадийной) будем называть реакцию, стехиометрическое уравнение которой можно записать «в одну строчку», в виде (3.18). На деле механизм реакции может оказаться сложным, она может проходить через ряд промежуточных стадий, но запись (3.18) означает, что в нашем рассмотрении их продукты не обнаруживаются (обычно из-за большой скорости промежуточных стадий). При более прецизионном исследовании та же реакция может предстать как сложная, однако сейчас ее можно считать простой. Часто понятие «формально простая» еще расширяют, распространяя его и на обратимые реакции; но в данном случае это не важно, потому что любая обратная реакция линейно зависит от прямой. При этом (3.18) может быть и той реакцией, которая нас интересует, и одной из стадий более сложной реакции. Обратим внимание на следующее. Уравнение (3.18) означает, что превращающиеся количества веществ пропорциональны их стехиометрическим коэффициентам. Поэтому для рассматриваемой одностадийной реакции (или стадии сложной реакции) отношение количества превратившегося вещества ∆g [моль] к стехиометрическому коэффициенту – одно и то же для всех веществ, следует лишь учитывать знаки ∆g и а:

∆g1 / a1 = ∆g2 / a2 = … = ∆gn / an = ζ. (3.19)

Величину ζ будем называть химической переменной. Если сложная реакция состоит из нескольких стадий, то протекание каждой из стадий характеризуется своей химической переменной, как правило, иной, чем переменные других стадий. (В различных источниках ζ называют также степенью завершенности стадии, числом пробегов стадии.) Основанный на химических переменных расчет позволяет вычислить количества неключевых веществ по начальному составу и известным количествам ключевых веществ. Однако, вопрос о том, сколько ключевых веществ следует задать, при этом, как правило, заранее не решается. Приведем пример, в котором будем считать, что реакция протекает гомогенно при постоянном объеме. Поэтому, рассмотрев единичный объем, можем считать, что количества веществ равны их концентрациям.

, инварианты химической реакции

где: - единичная матрица размерности ,

N– число веществ, N_K- число ключевых веществ,

С – вектор концентраций всех веществ.

Пример: число двойных связей при диспропорционировании олефинов. Если q инвариантов ЛН, то (n-q) свободных переменных (g_i) можно задать в качестве количеств ключевых реактантов (g_кл). Остальные q количеств (g_некл) вычисляют как решения системы уравнений инвариантов. Max q=RkH, соответствующее n_кл=RkA.

Рассмотрим формально одностадийную реакцию:

2 СН3 Br + Mg = C2 H6 + MgBr2 . (3.21)

В процессе реакции количества СH3 Br и Mg все время убывают, а количества C2 H6 и MgBr2 возрастают. Но существуют комбинации этих количеств, остающиеся неизменными (инвариантными). Эти комбинации называют инвариантами реакции. Так, для реакции (3.21) можно записать:

Нетрудно обнаружить физический смысл записанных выражений: inv1 – общее число молей квазиатомов СН3 в системе, которое, разумеется, не меняется; точно так же inv2 – число молей атомов Mg, а inv3 – атомов Br. Но и любая линейная комбинация этих величин тоже будет инвариантом.

Инварианты можно определить не только для одностадийных, но и для любых многостадийных реакций. Это делает их удобным инструментом анализа материальных превращений в реакционных системах. В частности, отмечу следующее. Пусть в реакционной системе имеется n веществ и пусть мы найдем q линейно независимых инвариантов. Тогда система инвариантов представляет собой q уравнений 1-й степени с независимыми левыми частями, содержащих n неизвестных. В этой системе можно выбрать (n – q) свободных переменных gкл, а оставшиеся q неизвестных gнекл будут найдены при заданных gкл как решение системы уравнений. Индексом «кл» здесь обозначены ключевые вещества, а индексом «некл» – неключевые. Таким образом, число неключевых веществ равно числу линейно независимых инвариантов q, а число ключевых равно n – q.

Инварианты – это величины, имеющие для данных условий совершенно определенные численные значения, не изменяющиеся по ходу реакции. В частности, в начальный момент их значения те же, и если известен начальный состав системы, то исходя из него легко их вычислить.

Наибольшее число линейно независимых инвариантов равно рангу атомной матрицы: q=r g h. (3.25)

Наибольшее число неключевых веществ равно q, а число ключевых

nкл=n – nнекл=n – q=r g a. (3.26)

Один из простейших способов построения системы линейно независимых инвариантов – тот, который без особых объяснений был применен при записи системы (3.22) – (3.24): каждый инвариант получается как уравнение материального баланса по одному из атомов или квазиатомов (по одному из столбцов атомной матрицы):

invr = Σ h_prg_p , (3.27) где суммирование ведется по столбцу r (по r-му атому); g_p – количество вещества A_p .

Ключевые и неключевые реактанты.

С + О2 = СО2 , (3.1)

С + СО2 = 2СО, (3.2)

2С + О2 = 2СО. (3.3)

Рассмотрим реакции (3.1) – (3.3). Пусть вначале в системе содержался 1 моль С и 1 моль О2 , оксидов не было. И пусть в некоторый момент установлено, что в системе находятся 0,1 моль С и 0,1 моль СО. Можно ли, исходя только из этих данных, рассчитать для того же момента количества непрореагировавшего О2 и образовавшегося СО2 ? Оказывается, можно. В реакцию вступило 1 – 0,1 = 0,9 моль С. Из него на образование СО затрачено 0,1 моль. Значит, на образование СО2 пошло 0,8 моль; количество диоксида в данный момент равно тоже 0,8 моль. Расход молекул О2 на образование СО равен 0,1/2 = 0,05 моль, а на образование СО2 – 0,8 моль. Всего затрачено 0,85 моль О2 , осталось 1 – 0,85 = 0,15 моль О2 . Мы рассчитали: в заданный момент в системе есть 0,8 моль СО2 и 0,15 моль О2 .

Те вещества, количества которых в данный момент заданы, называют ключевыми, а те, количества которых мы рассчитываем, – неключевыми. Заметим, что для начального момента должны быть известны количества и тех, и других веществ.

Любое из веществ, участвующих в реакции, может выступать в роли и ключевого, и неключевого. Чаще всего ключевыми оказываются те вещества, количества (или концентрации) которых проще измерить. Есть две основные ситуации, в которых желательно отнести часть веществ к неключевым. Это, во-первых, обстановка эксперимента или контроля производства. Во-вторых, это этап записи и решения уравнений математического описания процесса. В основе большинства этих уравнений лежат балансы по отдельным веществам. Число таких уравнений равно числу веществ, причем они могут оказаться достаточно сложными (нелинейными, дифференциальными), поэтому целесообразно уменьшить их число. Этого можно добиться, записывая и решая уравнения только для ключевых веществ, а количества остальных веществ рассчитывать через ключевые.

Степень превращения (конверсии), выход, селективность (, , ) по суммарному стехиометрическому уравнению.

Конверсия χ характеризует глубину превращения исходного реагента, выход η – количество образующегося продукта, селективность σ – то, насколько целесообразно использована та часть реагента, которая превратилась в продукты (какая часть прореагировавшего реагента превратилась именно в нужный продукт).

э=а_А/а_В – эквивалент продукта по реагенту. =(g_А0-g_А)/g_А0. =эg_В/g_А0. =эg_В/(g_А0-g_А). Связи =, =/, =/. Предельные значения.

Отсюда следует, что выход продукта равен степени превращения только при σ=1, т. е. при отсутствии побочных реакций, а во всех остальных случаях η < χ; далее, при χ=1 получаем η=σ, а при неполной конверсии η < σ. Как уже отмечалось, если реакция идет в гомогенной среде при постоянном объеме, то в формулах (3.33) – (3.35) можно заменить количества веществ на их концентрации.

э = аА / аВ коэффициент эквивалентности, который показывает, какому числу молей А эквивалентен один моль В.

Словесные определения как опора формульных.

Прямая задача химического равновесия. Обратная задача химического равновесия. Косвенные измерения. Нелинейное оценивание.

Одно из важнейших применений стехиометрического анализа – запись уравнений для расчета равновесия сложных (многостадийных) реакций. Такой расчет называют прямой задачей химического равновесия. Обратная задача равновесия формулируется так: получены опытные данные о свойствах систем, в которых установилось равновесие в интересующей нас реакции. Необходимо рассчитать константы равновесия для стадий этой реакции. Обычно мы можем измерить какие-то характеристики равновесного состава, зависящие от концентраций, причем чаще всего зависимость известна не полностью – мы не знаем ее параметров. И задача стоит в том, чтобы вычислить и неизвестные параметры этой зависимости, и константы равновесия.

Метод наименьших квадратов. Вариационное исчисление как общая теория методов оптимизации.

Метод наименьших квадратов - найти такие значения параметров, которые обеспечат минимум суммы

где суммирование производится по всем значениям i (номерам опытов).

Кинетика химических реакций. Механизм. Формальная кинетика химических реакций.

Скорость химического превращения r=dg_р/(Vdt). При постоянном объеме в закрытой системе r=dC/dt.

Главной проблемой кинетики как раздела физической химии является вопрос о механизме реакции. Основная задача – раскрыть механизм реакции и установить, как он отражается в кинетических закономерностях. При анализе, описании и расчете протекания реакции как элемента химико-технологического процесса вопрос о механизме часто не возникает: кинетические закономерности рассматриваются как уже заданные (например, изученные на предыдущем физико-химическом этапе исследования). В этих случаях описание проводится на языке формальной (феноменологической) кинетики.

Скорость реакции – основное понятие кинетики. Она определяется как количество вещества, реагирующее в единицу времени в единице реакционного пространства:

где r – скорость реакции; dgp – количество вещества, превращающееся в результате протекания реакции за время dt (знак дифференциала dgp определяется тем, образуется или расходуется вещество – соответственно знаки «+» и «–»); V – реакционное пространство (объем в случае гомогенной реакции, поверхность – в случае гетерогенной). Далее в этом разделе будут рассматриваться в основном гомогенные реакции, поэтому V обозначает объем.

Пользоваться уравнением (3.44) можно только при соблюдении двух условий: 1) реакция проходит при постоянном объеме; 2) объем этот можно считать закрытым.

Закрытой, или замкнутой, называется система, которая по ходу процесса не обменивается веществом с окружающей средой (хотя и может обмениваться энергией). Большинство химико-технологических процессов, и в первую очередь все непрерывные процессы, протекают в открытых системах, которые характеризует обмен с окружающей средой энергией и веществом. Именно открытость аппарата непрерывного действия (ввод и вывод потока) обеспечивает непрерывность процесса. Реактор чисто периодического действия открыт в периоды загрузки и выгрузки, а при протекании реакции он замкнут. Особенность уравнений материального баланса для замкнутых систем: вход и уход вещества равны нулю. Поэтому единственной причиной изменения количества вещества в системе dg является химическое превращение:

Смысл уравнения (3.47) следующий: в замкнутых гомогенных системах скорость реакции равна изменению концентрации во времени. Им часто пользуются, однако необходимо помнить, что это лишь частный случай, который верен далеко не для всех систем.

Формально простая реакция. Сложные реакции: обратимые, последовательные, параллельные, их комбинации. Независимость протекания реакций.

Химическая кинетика определяет простые (одностадийные) реакции как такие, которые по существу проходят в одну стадию; простая реакция содержит один элементарный акт. Однако такие реакции, которые проходят как истинно одностадийные, встречаются редко. В феноменологической кинетике оказывается удобным говорить о формально простых реакциях. Так называют реакции, которые можно формально пред ставить как протекающие в одну стадию. По существу реакция может быть сложной, проходящей через какие-то промежуточные стадии, но если в условиях рассматриваемой задачи промежуточные продукты не обнаруживаются, то реакция будет считаться формально простой.

Можно выделить три простейших типа сложных реакций.

1. Обратимая реакция: с излагаемой точки зрения она – сложная, состоящая из двух стадии: прямой и обратной реакций, хотя ряд авторов предпочитает говорить о них, как о частном случае формально простых реакций.

2. Параллельная реакция: исходное вещество по двум или нескольким параллельно протекающим реакциям (стадиям) превращается в два или несколько продуктов. Примером может служить нитрование толуола с параллельным получением о- и п-нитротолуолов.

3. Последовательная реакция: стадии реакции следуют одна за другой, продукт первой стадии является исходным веществом второй и т. д. Примером может служить полимеризация с последовательным присоединением молекул мономера к растущей макромолекуле.

Остальные сложные реакции можно представить в виде комбинаций указанных трех типов, например последовательно-параллельные, последовательные реакции с обратимыми стадиями и т. д.

Процесс протекания многостадийных реакций, стадии которых разделены во времени, т.е. сначала проводится одна стадия, затем через некоторое время – вторая и т. д считаются несколькими независимыми реакциями. А сложные реакции, которые перечислены в пунктах 1-3 (параллельная, последовательная, обратимая), проходят так, что в реакционной смеси одновременно идут все стадии и присутствуют исходные вещества и продукты всех стадий.

Скорость простой реакции (стадии) r=d/(Vdt) – определение ИЮПАК.

Рассмотрим формально одностадийную реакцию (она может быть и одной из стадий сложной реакции):

Возникает следующий вопрос: количество какого вещества (А, В или С) следует вводить в уравнение (3.44) при определении скорости реакции (3.48)? Ответ на этот вопрос легко получить из понятия стехиометрической эквивалентности. Если за какой-то промежуток времени прореагирует некоторое количество –dgA вещества А (знак минус означает, что вещество расходуется), то за это же время количества прореагировавшего В и образовавшегося С составят:

Поэтому, подставив в формулу (3.44) один раз dgA, другой раз dgB, третий раз dgC, получим три значения: rА, rB и rC, отличающиеся одно от другого постоянными множителями. Строго говоря, это одна и та же величина – скорость реакции (3.48), но выражена она в разных единицах. Для единообразия скорость одностадийной реакции, или скорость стадии, принято определять путем деления скорости, выраженной через любое вещество J, участвующее в данной стадии, на стехиометрический коэффициент этого вещества. В таком случае безразлично, какое из веществ принято в качестве J. Сопоставление с формулой (3.19) показывает, что скорость стадии можно записать через химическую переменную ζ:

Но при записи уравнений материального баланса важно пользоваться величинами скорости реакции, отнесенными к определенным веществам rJ . Такие скорости очень просто получаются из уравнений (3.50) и (3.19):

r_J = a_J r. (3.51)

здесь коэффициент a_J может быть как положительным, так и отрицательным или равняться нулю (например, если J – катализатор).

Порядок реакции по веществу, общий, константа скорости. r=kC_A^nAC_B^nB. Словесное обозначение. Уравнение Гульдберга и Вааге (не закон).

Скорость многих (хотя и не всех) формально простых реакций, в том числе многих стадий сложных реакций, пропорциональна концентрациям реагирующих веществ в некоторых степенях. Показатель степени в таком случае называют порядком реакции по реагенту. Так, для реакции

a_AA + a_BB → продукты

соответствующая зависимость будет выражаться кинетическим уравнением

где n1 – порядок реакции по веществу А; n2 – порядок реакции по веществу В. Сумму n1 + n2 называют общим, или суммарным, порядком. Коэффициент пропорциональности k именуют константой скорости реакции.

Порядок реакции или стадии буду иногда обозначать цифрой над (или под) стрелкой, указывающей направление реакции; здесь же приведу обозначение константы скорости. Так, запись

обозначает обратимую реакцию, у которой прямая стадия имеет 1-й порядок по А и константу скорости k1 , обратная – 2-й порядок по С и константу k2 . Поскольку порядок по В не указан, значит, он – нулевой.

Достаточно часты случаи, когда порядок по каждому из реагентов совпадает с его стехиометрическим коэффициентом. Но такое совпадение обязательно лишь для строго (не формально) простых реакций.

Закон действующих масс в кинетической форме (основное уравнение кинетики) гласит, что скорость элементарной химической реакции пропорциональна произведению концентраций реагентов в степенях, равных стехиометрическим коэффициентам в уравнении реакции. Это положение сформулировано учёными К. Гульдбергом и П. Вааге. Для элементарной химической реакции:

Температурная зависимость скорости реакции. Уравнение Аррениуса. k=Ae^-E/RT. lnk=lnA-E/RT. Предэкспоненциальный множитель и энергия активации – активационные параметры.

Порядок реакции иногда претерпевает изменения с ростом температуры, но это скорее исключение, чем правило. Наиболее тесно с температурой связана константа скорости реакции. Эта зависимость может быть описана уравнением Аррениуса:

Параметрами уравнения (3.53) являются предэкспоненциальный множитель, или предэкспонента, А и энергия активации Е.

Существует мнение, что чем больше энергия активации, тем, в соответствии с формулой (3.53), меньше величина k и, значит, медленнее реакция. Однако это мнение неверное. Величина k определяется совокупностью значений Е и А, поэтому сама по себе величина Е еще не определяет, быстро или медленно проходит реакция. В химической кинетике существует изокинетическое правило (правило компенсации): почти всегда чем больше энергия активации, тем больше предэкспонента. Реакция с меньшей Е имеет и меньшее значение А, а влияния обоих параметров противоположны. Формальный (феноменологический) смысл E иной. Прологарифмируем уравнение (3.53):

Получили линейную зависимость ln k от 1/Т, коэффициентами которой являются ln A и –E/R. Изобразим ее на графике для двух реакций: у первой величина E меньше (и, согласно изокинетическому правилу, ln A тоже меньше), чем у второй (рис. 3.1,а).

Из рис. 3.1,а очевидно, что при высоких температурах (значение 1/Т мало, область близка к оси ординат) больше константа скорости той реакции, у которой энергия активации больше. При низких температурах больше константа скорости реакции с малой энергией активации. Те же зависимости, но в координатах T – k представлены на рис. 3.1,б. Полученную закономерность можно сформулировать так: чем больше энергия активации, тем сильнее скорость реакции зависит от температуры. Такой характер влияния Е на прохождение реакции позволяет произвести быструю качественную оценку влияния температуры на ход некоторых сложных реакций. Так, для обратимых экзотермических реакций Е2 > Е1 : энергия активации обратной реакции больше, чем прямой. Поэтому с ростом температуры коэффициент k2 растет быстрее, чем k1 , в результате чего равновесие смещается влево. При эндотермических обратимых реакциях наоборот Е2 < Е1 , и с ростом температуры равновесие смещается вправо. Так устанавливается связь уравнения Аррениуса с правилом Ле Шателье.

Если рассматривается сложная реакция, некоторые стадии которой являются для нас побочными, то соотношение энергий активации различных стадий определяет влияние температуры на селективность: при нагревании преимущественно ускоряются те стадии, которые характеризуются большей энергией активации. Нужно иметь в виду, что в одном важном случае снижение энергии активации действительно приводит к ускорению реакции – это катализ. Механизм действия катализатора связан со снижением энергии активации реакции.

Конкуренция целевых и побочных стадий при изменении температуры. Суммирование по реакциям. r_j=Sum_i=1,mr_ji=Sum_i=1,ma_jir_i.

Для всех типов формально сложных реакций, кроме простейшей обратимой, понятие общей скорости реакции не имеет смысла. Реакция состоит из ряда стадий, каждая из них имеет свою скорость, и нельзя достаточно естественным образом определить, что такое скорость всей сложной реакции в целом. В то же время любое из участвующих в реакции веществ образуется или расходуется с определенной скоростью, причем знание этой скорости обязательно при расчете процесса. Скорость сложной реакции по любому веществу J равна алгебраической сумме скоростей всех стадий по этому веществу (с учетом стехиометрических коэффициентов):

Скорость стадии по веществу можно определить по формуле (3.51). Если вещество в стехиометрии стадии не участвует, его стехиометрический коэффициент в этой стадии равен нулю.

Прямая и обратная задача химической кинетики.

Прямая задача химической кинетики – расчет зависимости от времени концентраций веществ в реакционной смеси при известных кинетическом уравнении, значениях констант скорости, начальном составе. Особенность таких задач состоит в том, что перечисленных данных недостаточно. Необходимо учесть также характер движения потока, в котором проходит реакция, а в случаях гетерогенных реакций также характер диффузии веществ в зоне реакции.

Обратные задачи кинетики имеют очень сложную специфику. Дело в том, что, как уже отмечалось, реально все химические реакции сложны, проходят через ряд промежуточных стадий. Обратная задача заключается в расшифровке механизма реакции, определении ее маршрута: стадий, через которые она проходит, и кинетических характеристик этих стадий. Обратная задача может быть сформулирована как задача дискриминации : нужно отбросить все механизмы, кроме одного истинного. Из-за того что предполагаемых механизмов много, часть из них, в том числе и далеких от истинного механизма, может показывать результаты, близкие к истинным. Решение таких задач требует больших объемов исследования, применения специальных методов планирования эксперимента и метода наименьших квадратов в варианте нелинейного оценивания.

Качественный анализ хода реакции. Асимптотические оценки. Правило Лопиталя. Температурная зависимость в качественном анализе.

Одна из возможностей качественного анализа опирается на асимптотические оценки – оценки поведения функций в крайних областях значений аргумента. В рассматриваемом случае целесообразно в качестве аргумента принять время t, причем крайние области его значений – это t = 0 и t → ∞.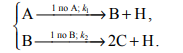

В качестве примера проанализируем протекание реакции. Целевым продуктом является вещество В. Примем следующие условия. Реакция проходит в замкнутой системе (можно показать, что качественные выводы окажутся такими же и для открытой системы, но для замкнутой анализ проще). Объем и температура постоянны. Начальная концентрация реагента сА0= 1 моль/л. В начале процесса продукты отсутствуют. Известны энергии активации первой и второй стадий: Е1 = 45000 и Е2 = 75000 Дж/моль соответственно. Вначале выясним, какими станут концентрации веществ, если время процесса очень велико (t → ∞). При этом обе реакции дойдут до конца, поскольку и та, и другая необратимы. Веществ А и В не останется, а концентрации С и Н определятся стехиометрией: 2 и 2 моль/л.

Затруднение возникает при оценке предела σ, когда t→ 0. Формулы (3.35) и (3.36) приводят к выражению вида 0/0, т.е. к неопределенности. Раскрыть эту неопределенность можно по правилу Лопиталя, заменив функции в числителе и знаменателе их производными по времени. Для замкнутой системы производная от концентрации по времени равна скорости реакции. При этом учтем, что начальная концентрация – величина постоянная (в данном случае равная 1), а производная от постоянной равна 0. Учтем также то, что при t → 0 cB → 0. Получаем: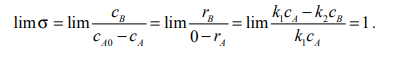

Можно показать, что и в открытой системе предел окажется таким же. Физический смысл этого результата прост. При малом времени процесса скорость первой стадии реакции высока, так как велика концентрация А, а скорость второй стадии очень мала (из-за малости сВ) и стремится к 0 при t → 0. Поэтому в пределе реакция проходит так, как будто побочной стадии нет; а в отсутствие побочной стадии селективность равна 1. Если бы побочная стадия была параллельной, рассматриваемый предел был бы меньше 1. Зная величины констант скорости, его можно было бы рассчитать; в противном случае пришлось бы констатировать, что селективность стремится к некоторой величине σ0 , причем 0 < σ0 <1.

Полученные нами асимптотические оценки не содержат температуры ни в явном, ни в неявном виде. Это верно для рассматриваемой реакции, но в других случаях выражения для пределов могут содержать константы скорости или константы равновесия – тогда температура будет влиять и на асимптотические оценки. Для рассматриваемой реакции пределы при любых температурах одни и те же, изменяются характеристики зависимостей между этими пределами. Для показателей χ и σ изменения просты. С ростом температуры скорость первой стадии реакции растет, поэтому кривая для χ вначале идет круче и быстрее приближается к предельному значению. Скорость второй стадии реакции, обусловливающей падение селективности, тоже растет, и кривая зависимости σ(t) падает круче сначала и быстрее переходит в область очень малых значений. Что же касается зависимости η(t), то здесь наибольший интерес представляет точка максимума, обе ее координаты – время достижения максимума и максимальное достигаемое значение η. Для качественной оценки влияния температуры на время достижения максимума достаточно учесть, что с ростом температуры ускоряются обе стадии. При этом выход продукта будет быстрее расти и быстрее падать – максимум сместится к меньшему времени. Чтобы оценить, как при этом изменится высота максимума, учтем следующее. Искомая высота определяется конкуренцией обеих стадий: первая увеличивает η, вторая уменьшает. С ростом температуры обе стадии ускоряются, но вторая – сильнее, потому что Е2 > Е1 . В результате повышение температуры приведет к снижению максимального значения η.