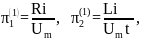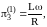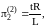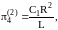2.3.2 Вторая форма записи

По аналогии с пунктом 2.3.1 определим вторую форму записи крите­риев подобия. Возьмём определитель третьего порядка отличный от нуля:

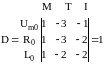
Независимыми параметрами во второй форме записи будут , и . Остальные параметры будут зависимы и будут выражаться через независи­мые. Найдем соотношения между зависимыми и независимыми парамет­рами. Они будут иметь следующий вид:

(12)

Далее задача заключается в нахождении показателей , ,…, .

; ;

; ;

; ;

; ;

; ;

; ;

; ;

.

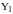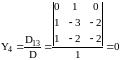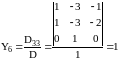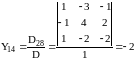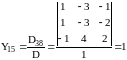После подстановки найденных значений , ,…, в систему (12), получаем:

Учитывая, что связь между единицами измерения идентична связи между самим физическими величинами, мы можем записать следующее:

Так как , и независимые величины, то мы можем выбрать их произвольно. Выберем их таким образом:

Подставляя выбранные значения в выражение (8) вместо входящих в него параметров, получим:

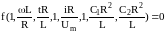(13)

На основании первой теоремы подобия все отношения, отличные от еди­ницы и входящие в выражение (15), представляют собой критерии подо­бия во второй форме записи.

, , , , .

2.3.3 Третья форма записи

Определим третью форму записи критериев подобия. Возьмём определи­тель третьего порядка отличный от нуля:

Независимыми параметрами в третьей форме записи будут , и . Остальные параметры будут зависимы и будут выражаться через независи­мые. Найдем соотношения между зависимыми и независимыми параметрами. Они будут иметь следующий вид:

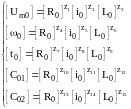(14)

Далее задача заключается в нахождении показателей , ,…, .

; ;

; ;

; ;

; ;

; ;

; ;

; ;

.

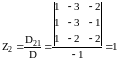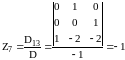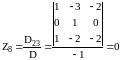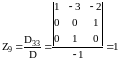После подстановки найденных значений , ,…, в систему (14), получаем:

Учитывая, что связь между единицами измерения идентична связи между самим физическими величинами, мы можем записать следующее:

Так как , и независимые величины, то мы можем выбрать их про­извольно. Выберем их таким образом:

Подставляя выбранные значения в выражение (8) вместо входящих в него параметров, получим:

(15)

На основании первой теоремы подобия все отношения, отличные от еди­ницы и входящие в выражение (15), представляют собой критерии подо­бия в третьей форме записи.

, , , , .

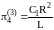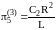Заключение

В проделанной расчетно-графической работе для процесса, описанного дифференциальным уравнением, были определены критерии подобия спосо­бом интегральных аналогов и на базе -теоремы, которые приведены в таб­лице 3.

Метод интегральных аналогов не даёт все возможные формы записи крите­риев подобия, в отличие же от определения их на базе π-теоремы.

Таблица 3. Сводная таблица критериев подобия.

№ формы записи	Метод интегральных анало­гов	На базе π-теоремы
1
2
3
4
5