Липецкий государственный технический университет

Кафедра электрооборудования

РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ

По моделированию в технике

«Определение критериев подобия способом интегральных аналогов и на базе π-теоремы»

Студент Фролов С.Н.

Группы ЭО142

Руководитель

Доцент Бойчевский В. И.

Липецк 2016 г.

Оглавление

Задание на расчетно-графическое задание 3

1 Определение критериев подобия способом интегральных аналогов 4

1.1 Первая форма записи 4

1.2 Вторая форма записи 5

1.3 Третья форма записи 6

1.4 Четвёртая форма записи 6

1.5 Пятая форма записи 7

2 Определение критериев подобия на базе π-теоремы 9

2.1 Составление таблицы размерностей параметров процесса……………… 9

2.2 Определение числа независимых параметров процесса и количества возмож­ных форм записи критериев подобия 10

2.3 Определение критериев подобия в трех формах записи…………………. 11

2.3.1 Первая форма записи 11

2.3.2 Вторая форма записи 14

2.3.3 Третья форма записи 17

Заключение 21

Список литературы 23

Приложение. Определители третьего порядка 24

Задание на расчетно-графическое задание

Для процесса, описываемого дифференциально-интегральным уравне­нием, приведенным согласно варианта в таблице, определить критерии подо­бия[2]:

1 Способом интегральных аналогов во всех возможных формах записи;

2 На базе π-теоремы в любых трех формах записи из всех возмож­ных.[2]

Таблица 1. Исходные данные к расчетно-графическому заданию.

№ Варианта	Дифференциально-интегральное уравнение энергетического процесса
31

1 Определение критериев подобия способом интегральных аналогов

Определим число критериев подобия и число форм их записи:

= n = 5

Перенесем все члены уравнения в одну сторону:

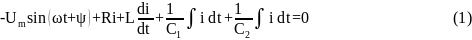
1.1 Первая форма записи

Найдем критерии подобия в первой форме записи. Для этого разделим все члены уравнения (1) на первый член, то есть на :

Исключаем знаки дифференцирования и неоднородные функции из уравне­ния (2). Получаем выражение:

В соответствии с первой теоремой подобия имеем пять критериев подо­бия. Четыре из них являются основными и имеют пять форм записи, и один дополнительный критерий подобия, который всегда имеет единствен­ную форму записи.

Запишем критерии подобия в первой форме:

;

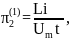
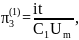
1.2 Вторая форма записи

Проделаем те же вычисления, которые были приведены в пункте 1.1 для второй и последующих форм записи. Разделим все члены уравнения (1) на :

После математических преобразований выражения (3) и исключения из него знаков дифференцирования и неоднородных функций, получаем:

Запишем найденные критерии подобия во второй форме:

;

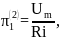
1.3 Третья форма записи

Разделим все члены уравнения (1) на

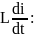
Преобразуем выражение (4), исключая из него все знаки дифференцирова­ния и неоднородные функций, получаем:

Запишем найденные критерии подобия в третьей форме:

;

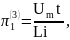
1.4 Четвертая форма записи

Разделим все члены уравнения (1) на

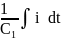
Преобразуем выражение (5), исключив из него знаки дифференцирова­ния и неоднородные функции, получаем:

Запишем найденные критерии подобия в четвертой форме записи:

;