- •111Equation Chapter 1 Section 1Липецкий государственный технический университет
- •1 Определение критериев подобия способом интегральных аналогов
- •1.1 Первая форма записи
- •1.2 Вторая форма записи
- •1.3 Третья форма записи
- •2 Определение критериев подобия на базе π-теоремы
- •2.1 Составление таблицы размерностей параметров процесса
- •2.2 Определение числа независимых параметров процесса и количества возможных форм записи критериев подобия
- •2.3 Определение критериев подобия в трех формах записи
- •2.3.1 Первая форма записи
- •2.3.2 Вторая форма записи
- •2.3.3 Третья форма записи
- •Окончание таблицы 3.
111Equation Chapter 1 Section 1Липецкий государственный технический университет
Кафедра: Электрооборудования
РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ
по моделированию в технике
«Определение критериев подобия способом интегральных аналогов и на базе π-теоремы»
Студент Бурцев А.А.
Группы ЭО142
Руководитель
Доцент Бойчевский В. И.
Липецк 2016 г.
Оглавление
Задание на РГЗ 3
1 Определение критериев подобия способом интегральных аналогов 4
1.1 Первая форма записи 4
1.2 Вторая форма записи 5
1.3 Третья форма записи 5
1.4 Четвёртая форма записи 6
2 Определение критериев подобия на базе π-теоремы 7
2.1 Составление таблицы размерностей параметров процесса……………… 7
2.2 Определение числа независимых параметров процесса и количества возможных форм записи критериев подобия 8
2.3 Определение критериев подобия в трех формах записи…………………. 9
2.3.1 Первая форма записи 9
2.3.2 Вторая форма записи 12
2.3.3 Третья форма записи 15
Заключение 19
Список литературы 21
Приложение Определители 22
Задание на РГЗ
Для процесса, описываемого дифференциально-интегральным уравнением, приведенным согласно варианта в таблице, определить критерии подобия:
1 Способом интегральных аналогов во всех возможных формах записи;
2 На базе π-теоремы в любых трех формах записи из всех возможных.
Таблица 1. Исходные данные к расчетно-графическому заданию.
№ Варианта |
Дифференциально-интегральное уравнение энергетического процесса |
19 |
|
1 Определение критериев подобия способом интегральных аналогов
Определим число критериев подобия и число форм их записи:
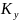 =
n
– 1 + a
= 4 – 1 + 1 = 4
=
n
– 1 + a
= 4 – 1 + 1 = 4
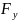 =
n
= 4
=
n
= 4
Перенесем все члены уравнения в одну сторону:
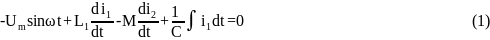
1.1 Первая форма записи
Найдем
критерии подобия в первой форме записи.
Для этого разделим все члены уравнения
(1) на первый член, то есть на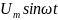 :
:
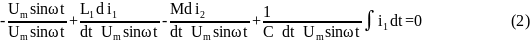
Исключаем знаки дифференцирования и неоднородные функции из уравнения (2). Получаем выражение:
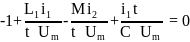
В соответствии с первой теоремой подобия имеем пять критериев подобия. Четыре из них являются основными и имеют пять форм записи, и один дополнительный критерий подобия, который всегда имеет единственную форму записи.
Запишем критерии подобия в первой форме:
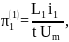
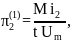
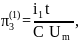
 ;
;
1.2 Вторая форма записи
Проделаем
те же вычисления, которые были приведены
в пункте 1.1 для второй и последующих
форм записи. Разделим
все
члены
уравнения
(1) на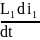 :
:
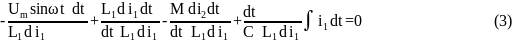
После математических преобразований выражения (3) и исключения из него знаков дифференцирования и неоднородных функций, получаем:
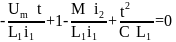
Запишем найденные критерии подобия во второй форме:

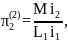
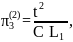
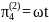
1.3 Третья форма записи
Разделим
все члены уравнения (1) на
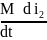 :
:
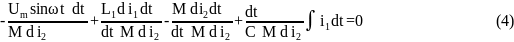
Преобразуем выражение (4), исключая из него все знаки дифференцирования и неоднородные функций, получаем:
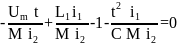
Запишем найденные критерии подобия в третьей форме:
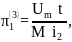
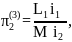
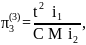
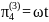 ;
;
1.4 Четвертая форма записи
Разделим
все члены уравнения (1) на
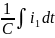
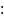
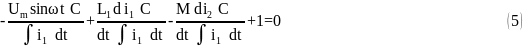
Преобразуем выражение (5), исключив из него знаки дифференцирования и неоднородные функции, получаем:
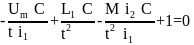
Запишем найденные критерии подобия в четвертой форме записи:
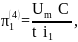
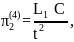
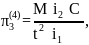
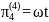 ;
;