
Экзамен / ММвСС. Экзаменационные вопросы и ответы
.pdf
44. Численные методы оптимизации. Общая структура алгоритма. Привести примеры численных методов условной и безусловной оптимизации.
Численный метод представляет собой итерационную циклическую процедуру, на каждом цикле которой производится выбор нового значения переменной (согласно некоторому методу), вычисление значения оптимизируемой функции и проверка критерия сходимости. Циклы повторяются, пока не выполнен критерий сходимости.
Численные методы оптимизации:
•Безусловная оптимизация (функции одной переменной, функции нескольких переменных).
•Условная оптимизация (функции нескольких переменных).
Оптимизация функции одной переменной:
•Прямой поиск (безусловная оптимизация)
•Дихотомия
•Метод золотого сечения
•Метод чисел Фибоначчи
•Метод квадратичной интерполяции
Оптимизация функции нескольких переменных:
•Детерминированные методы:
oПокоординатный спуск
oМетод Хука-Дживса
oСимплекс метод Нелдера-Мида
oКомплексный метод Бокса
oМетод штрафных функций
•Стохастические методы:
oСлепой случайный поиск
oЭволюционный метод (генетический алгоритм)
45.Оптимизация функции одной переменной. Метод дихотомии.
Задана функция одной переменной ( ). [ , ]. Абсолютная погрешность: |
∆ |
. |
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Требуется найти экстремум 0 |
= arg min ( ) или 0 = arg max ( ). |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поиск экстремума |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Формализация |
||||
|
|
Алгоритм поиска представляет собой |
|
|
(для реального кода): |
|||||||
|
|
ПОКА (| – | ≥ ) { |
||||||||||
|
|
много итерационную процедуру: |
||||||||||
|
|
|
|
|
− |
|||||||
|
|
• |
На каждой итерации интервал |
__ 1 |
= + |
|||||||
|
4 |
|
|
|
||||||||
|
|
|
поиска экстремума сужается путем |
__ 2 |
= − |
− |
||||||
|
|
|
исключения правого ( 2, ) или |
4 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
__ЕСЛИ ( ( 1) > ( 2)) |
|||||||||
|
|
|
левого отрезка ( , 1). |
|||||||||
|
|
|
____ = 1 |
|
|
|
|
|||||
|
|
• |
Правый отрезок исключается если |
|
|
|
|
|||||
|
|
__ИНАЧЕ ЕСЛИ ( ( 1) < ( 2)) |
||||||||||
|
|
|
( 1) < ( 2). |
|||||||||
|
|
|
____ = 2 |
|
|
|
|
|||||
|
|
• |
Левый отрезок исключается если |
|
|
|
|
|||||
|
|
__ИНАЧЕ { |
||||||||||
|
|
|
( 1) > ( 2). |
|||||||||
|
|
|
____ = 1 |
|
|
|
|
|||||
|
|
• |
Итерации повторяются пока | − |
|
|
|
|
|||||
|
|
____ = 2 |
|
|
|
|
||||||
|
|
|
| > = . |
|
|
|
|
|||||
|
|
|
__} |
|
|
|
|
|
||||
|
|
|
|
+ |
|
|
|
|
|
|
||
|
|
• |
Результат = |
. |
} |
|
|
|
|
|
||
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
РЕЗУЛЬТАТ = |
|
|||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
||
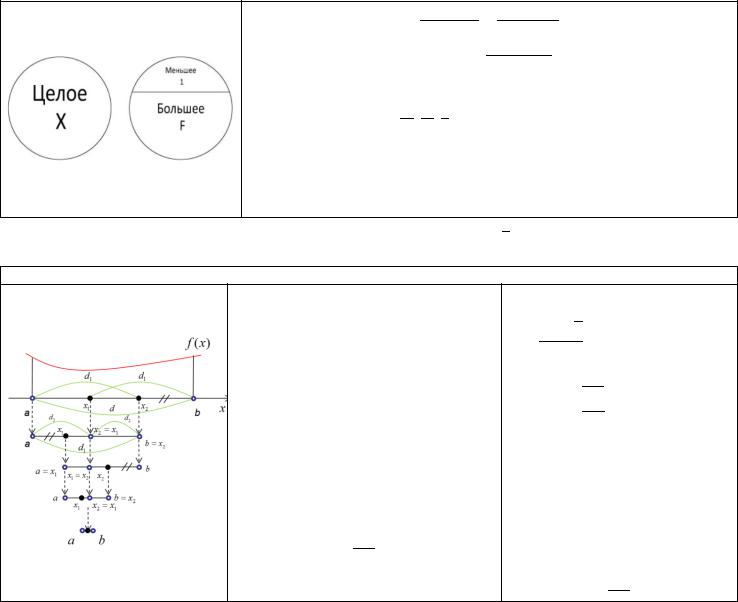
46. Оптимизация функции одной переменной. Метод золотого сечения.
Золотое сечение — это такое деление целого на 2 части, при котором отношение большего к меньшему равно отношению целого к большему (62% / 38%).
Целое Большее
Большее = Меньшее
Большее2 Целое = Меньшее
= 2
Получена последовательность: 1, , 2.
Её можно продлить: … , 13 , 12 , 1 , 1, , 2, 3, … Особенности ряда:
•Каждый следующий член ряда равен сумме двух предыдущих
•Каждый следующий член ряда равен предыдущему, умноженному на
2 = + 1 2 − − 1 = 0= . = Ф, 2 = −0.618
Задана функция одной переменной ( ). [ , ]. Абсолютная погрешность: ∆2.
Требуется найти экстремум 0 |
= arg min ( ) или 0 |
= arg max ( ). |
|
|
|
Поиск экстремума
Алгоритм поиска представляет собой много итерационную процедуру:
•На каждой итерации интервал поиска экстремума сужается путем
исключения правого ( 2, ) или левого отрезка ( , 1).
•Правый отрезок исключается если
( 2) > ( 1).
•Левый отрезок исключается если
( 1) > ( 2).
•Итерации повторяются пока | −| > = .
•Результат = +2 .
Формализация
(для реального кода):
Φ = 1 + √5 = 1.618.. 2
ПОКА (| – | ≥ ) {
__ 1 = − Φ− __ 2 = + Φ−
__ЕСЛИ ( ( 1) > ( 2))
____ = 1
__ИНАЧЕ ЕСЛИ ( ( 1) < ( 2))
____ = 2
__ИНАЧЕ {
____ = 1
____ = 2 __}
}
РЕЗУЛЬТАТ = +
2
47. Оптимизация функции нескольких переменных. Безусловная оптимизация. Покоординатный спуск.
Пусть задана выпуклая функция переменных ( ) = ( 1, 2, … , ). Данный метод предполагает следующие шаги:
1.Фиксируются все значения переменных кроме одной.
2.Производится поиск экстремума по одной переменной одним из известных методов.
3.Найденное значение присваивается данной переменной и для поиска выбирается следующая переменная.
4.После нахождения экстремумов по каждой из переменных проверяется критерий сходимости. Если условие сходимости не выполняется, то к 1, если выполняется, то полученные значения переменных и принимаются как
искомый экстремум.
Данный метод может быть эффективен только при оптимизации относительно простых функций.

Пример (из лекции)
Функция Розенброка
( ) = (1 − 1)2 + 100( 2 − 12)2
Шаги поиска экстремума (на каждом из шагов используется метод золотого сечения)
Результат: 0 = (1.16, 1.36).
Вывод: маленькая точность. Должно быть (1,1). Потребовалось около 1138x20 вычислений функции.
48. Оптимизация функции нескольких переменных. Безусловная оптимизация. Симплекс метод Нелдера-Мида (поиск по деформируемому многограннику).
Пусть задана выпуклая функция переменных ( ) = ( 1, 2, … , ). Данный метод предполагает следующие шаги:
1.Подготовка. Задается исходный многогранник, содержащий + 1 вершину (т.е. + 1 точка – симплекс).
2.Оценка. Вычисляются значения функции в вершинах многогранника. Находят «худшую» , «лучшую» , и предшествующую «худшей» (по величине) вершину .
3.Отражение. Относительно «наихудшей» точки определяется центр тяжести противоположной грани. Выполняется попытка отражения наихудшей точки через найденный центр тяжести. В результате чего получают точку .
4.Растяжение. Если отраженная точка «лучше» «лучшей», то делается попытка растянуть многогранник в данном направлении. Если растяжение успешное, то полученная точка включается в список вершин многогранника, в противном случае в список вершин включается отраженная точка .
5.Сокращение. Сокращение производится, если отраженная точка хуже точки . Если лучше , то выполняется внешнее сокращение, в результате которого получают точку 1. Если хуже выполняется внутреннее сокращение , в результате которого получают точку 2. Если ( 1) или ( 2) < ( ), то соответствующая точка включается в список вершин.
6.Перемещение. Включенная в многогранник точка замещает наихудшую точку . Точка исключается, этим достигается перемещение многогранника.
7.Сжатие. Сжатие многогранника производится во всех направлениях. При этом лучшая вершина остается на месте, а остальные пересчитываются.
8.Проверка сходимости. Вычисляется среднеквадратическое отклонение значений функции в вершинах многогранника. Если вычисленное значение меньше заданной величины, то сходимость достигнута.
Пример (из лекции)
Функция Розенброка
( ) = (1 − 1)2 + 100( 2 − 12)2

Шаги поиска экстремума из точки (3,3)
Результат: 0 = (1.000, 1.002).
Вывод: высокая точность. Должно быть (1,1). Потребовалось всего 243 вычислений функции.
49. Оптимизация функции нескольких переменных. Условная оптимизация. Метод штрафных функций.
Метод заключается в замене исследуемой функции некоторой модифицированной функцией, которая в области допустимых значений близка к исходной функции, а вблизи области ограничений ее значение резко увеличивается. Задача: минимизировать функцию ( ) при ограничениях ( ) ≥ 0, = 1 … .
Начальный этап.
Выбрать > 0 в качестве константы остановки, начальную допустимую точку , для которой ( ) > |
|||
|
|
|
|
0, = 1 … , скаляр 0 |
и 0 < < 1. Положить = 1 и перейти к основному этапу. |
||
Основной этап. -тая итерация. |
|
|
|
1. При исходной точке решить следующую задачу оптимизации: |
|
|
|
|
|
|
|
|
|
|
|
|
( , ) = ( ) + ( ) = ( ) + ∑ ( |
( )) |
|
|
|
|
|
|
=1 |
|
|
Минимизировать, где > 0 – параметр, значение которого убывает с каждой итерацией ( ) → ∞ при → |
|||||||||
|
|
|
|
|
|
|
|
|
|
0, – положительные весовые коэффициенты, ( ) = ∑ |
( |
( )) . |
|||||||
|
|
|
|
|
=1 |
|
|
|
|
Примерами штрафных функций являются: |
|
|
|
|
|
|
|
||
|
1) |
Обратная функция: ( ( )) = |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
( ) |
|
|
|
||
|
|
|
|
|
|
|
|||
|
2) |
Логарифмическая функция: ( |
( )) = − ln ( ). |
||||||
|
|
|
|
|
|
|
|
|
|
Положить |
равным оптимальному решению задачи минимизации и перейти ко второму шагу. |
||||||||
+1 |
|
|
|
|
|
|
|
|
|
2.Если ∑=1 ( ( )) < , то остановиться. Решение является искомым.
Иначе положить +1 = . Изменить = + 1 и перейти к первому шагу ( + 1)-й итерации.
Пример (из лекции)
( ) = 2
( ): > 2 − 2 > 0( , ) = 2 + 1
− 2

Пример на C++
Программа нахождения минимума функции Розенброка.
// C++14
#include <iostream> #include <cmath> #include <functional> #include <algorithm> using namespace std;
//Константы: точность и макс. кол-во итераций const double EPS = 1e-8;
const int ITERATIONS = 10000;
//Функция Розенброка
double f(double x, double y) {
return (1.0 - x) * (1.0 - x) + 100 * (y - x * x) * (y - x * x);
}
// Требование 1: x > 3
double psi_1(double x, double y) { return x - 3;
}
// Требование 2: y > 3
double psi_2(double x, double y) { return y - 3;
}
// Покоординатный спуск как часть метода штрафных функций
void minimize(int k, double &x, double &y, std::function<double(double, double)> &func) { double phi = (1.0 + sqrt(5.0)) / 2.0; // золотое сечение
double startX = x - x / (k * phi), stopX = x + x / (k * phi); double startY = y - y / (k * phi), stopY = y + y / (k * phi); for (int i = 0; i < ITERATIONS; ++i) {
if (i % 2 == 0) { // оптимизируем X double a = startX, b = stopX; while (fabs(b - a) >= EPS) {
double x1 = b - (b - a) / phi, x2 = a + (b - a) / phi; double f1 = func(x1, y), f2 = func(x2, y);
a = (f1 >= f2) ? x1 : a; b = (f1 <= f2) ? x2 : b;
}
x = a + (b - a) / 2.0;
}
else { // оптимизируем Y
double a = startY, b = stopY; while (fabs(b - a) >= EPS) {
double y1 = b - (b - a) / phi, y2 = a + (b - a) / phi; double f1 = func(x, y1), f2 = func(x, y2);
a = (f1 >= f2) ? y1 : a; b = (f1 <= f2) ? y2 : b;
}
y = a + (b - a) / 2.0;
}
}
}
// Метод штрафных функций int main() {
int i = 1;
//координаты начальных точек следует устанавливать больше, чем может находится экстремальная точка, например, (20, 20); Экстремальная точка находится f(3, 9) = 4.
//значение r устанавливается равным 1
//b в данном случае характеризует приоритет ограничений: чем больше, тем выше вероятность соблюдения ограничений, но 0 < b < 1
double point_x = 20, point_y = 20, r = 1.0, b = 0.7;
//Создаем указатель на функцию типа "double func(double, double)".
std::function<double(double, double)> func; do {
cout << point_x << ' ' << point_y << " -> " << f(point_x, point_y) << endl;
//Меняем функцию в соответствии со значением r func = [r] (double x, double y) {
return f(x, y) + r / psi_1(x, y) + r / psi_2(x, y);
};
//Минимизируем
minimize(i, point_x, point_y, func); r *= b;
++i;
} while (i < ITERATIONS && func(point_x, point_y) >= EPS); cout << "Result: " << endl;
cout << point_x << ' ' << point_y << " -> " << f(point_x, point_y); return 0;
}
20 20 -> 1.44404e+007 |
|
||
7.63932 |
32.3607 |
-> 67636.5 |
|
5.27864 |
27.8641 |
-> 18.3068 |
|
4.70318 |
22.1237 |
-> 13.715 |
|
4.32455 |
18.7054 |
-> 11.054 |
|
4.04842 |
16.3933 |
-> 9.29417 |
|
3.83421 |
14.7047 |
-> 8.034 |
|
3.66101 |
13.4064 |
-> 7.08215 |
|
3.51673 |
12.3707 |
-> 6.33504 |
|
3.39381 |
11.5212 |
-> 5.7314 |
|
3.28726 |
10.8092 |
-> 5.23251 |
|
3.19359 |
10.2019 |
-> 4.81264 |
|
3.11036 |
9.67643 |
-> 4.45406 |
|
3.058 9.35139 -> 4.23538 |
|
||
3.04864 |
9.29419 |
-> 4.19691 |
|
3.04077 |
9.24628 |
-> 4.16474 |
|
3.03416 |
9.20615 |
-> 4.13782 |
|
3.02862 |
9.17255 |
-> 4.11531 |
|
3.02397 |
9.14442 |
-> 4.09647 |
|
3.02008 |
9.12087 |
-> 4.08071 |
|
3.01681 |
9.10115 |
-> 4.06753 |
|
3.01407 |
9.08465 |
-> 4.0565 |
|
3.01178 |
9.07083 |
-> 4.04727 |
|
3.00986 |
9.05927 |
-> 4.03955 |
|
3.00825 |
9.0496 -> 4.03309 |
|
|
Result: |
|
|
|
3 9 -> 4 |
|
|
|
|
Wolfram Alpha: { (1 − )2 |
+ 100 ( − 2)2 } { > 3, > 3 } = 4 ( , ) = (3, 9) |
|
50. Оптимизация функции нескольких переменных. Невыпуклые функции. Эволюционный метод (генетический алгоритм).
Стохастические методы.
Целью разработки и использования данных методов является оптимизация невыпуклых функций.
Общего метода численной оптимизации невыпуклых функций не существует. Существуют лишь подходы, позволяющие на основании имеющихся сведений об оптимизируемой функции использовать те или иные методы, позволяющие с достаточной уверенностью находить оптимальные (или приемлемые) решения.
Оптимизацию невыпуклых функций называют многоэкстремальной оптимизацией. Примеры методов оптимизации:
•Слепой случайный поиск: поиск экстремума в заданной области путем проб в случайных точках области;
•Локальный случайный поиск: поиск экстремума в заданной области путем проб в случайных точках, сосредоточенных вокруг некоторой базисной точки с последующим переходом к другой базисной точке;
•Мультистартовый метод: многократный запуск метода поиска экстремума выпуклой функции из различных стартовых точек;
•Эволюционный метод (генетический алгоритм): метод имитирующий процесс эволюции, происходящий в
живой природе.
Генетический алгоритм (англ. genetic algorithm) — это стохастический эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём последовательного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию. Является разновидностью эволюционных вычислений (англ. evolutionary computation). Отличительной особенностью генетического алгоритма является акцент на использование оператора «скрещивания», который производит операцию рекомбинации решений-кандидатов, роль которой аналогична роли скрещивания в живой природе.
Предполагает имитацию процесса эволюции (различные реализации могут использовать различные приемы имитирующие этапы эволюционного процесса). Например:
•Значения переменных (точка) – особь.
•Значение функции в точке характеризует приспособленность особи (выживаемость).
Пусть задана выпуклая функция переменных ( ) = (1, 2, … , ).
Данный метод предполагает следующие шаги:
1.Создание начальной популяции – множества особей, численность .
2.Выбор родителей. Полагаем, что для появления новой особи требуются наследственные признаки двух других особей. Выбор может производится различными способами, например, случайно (панмиксия). Особи и .

3.Рекомбинация. Передача наследственных признаков потомку. Существуют различные способы реализации данного шага. Например, вектор переменных можно рассматривать как набор генов, при этом одноименные гены родителей объединяются со случайными коэффициентами:
= ( ) + (1 − ) ( ), где = 0 … 1 – случайное число.
4.Мутация. Случайное изменение наследственных признаков. Например, = , где (дзета) – случайный коэффициент.
5.Селекция. Новая особь помещается в популяцию на место наименее приспособленной особи, которая,
освобождая позицию, погибает.
Сходимость. Процесс смены поколений повторяется пока на протяжении некоторого (заданного) числа поколений не будет происходить уменьшение (увеличение) значения целевой функции.
Пример (из лекции)
Функция Экли
( , ) = −20 exp (−0.2√0.5( 2 + 2)) − exp(0.5(cos(2 ) + cos(2 ))) + + 20
Найденное значение:
= (−0.002, −0.014), ( ) = 0.040
Размер популяции 50, число поколений 1000.
Реальный экстремум:
= (0, 0), ( ) = 0

Пример на C++
Программа с генетическим алгоритмом поиска глобального минимума функции двух переменных ( , ) в виде класса со свойствами и методами.
Представлены вычисления следующих функций7:
•Функция Экли
•Функция Била
•Функция Изома
•Функция Розенброка
•Функция Шаффера N2
// C++14
#define _USE_MATH_DEFINES #include <cmath> #include <algorithm> #include <iostream> #include <functional> #include <vector> #include <random> #include <stack> #include <iomanip>
using namespace std;
template <class T> class GeneticAlgorithm { public:
// Инициализация основных переменных в конструкторе
GeneticAlgorithm(int number_of_population_members, double percent_of_best_ones_to_live, pair<T, T> section, std::function<T(T, T)> function, double probability)
:number_of_population_members_(number_of_population_members), percent_of_best_ones_to_live_(percent_of_best_ones_to_live), section_(std::move(section)), function_(std::move(function)),
probability_(probability) { std::random_device rd; random_gen_.seed(rd());
}
// Инициализирует популяцию
void generateInitialPopulation() { population_x_ = createNewPopulation(); population_y_ = createNewPopulation();
}
//Создает и возвращает новую популяцию vector<T> createNewPopulation() {
T minimum = section_.first; T maximum = section_.second;
vector<T> result(number_of_population_members_);
std::uniform_real_distribution<> real_dist(minimum, maximum); // Равномерное непрерывное распределение for (auto &k : result) {
k = real_dist(random_gen_);
}
return result;
}
//Фитнес-функция (или функция пригодности)
//Возвращает пары векторов лучших популяций X и Y (отбор по проценту выживаемости)
pair<vector<T>, vector<T>> getBestMembers() {
vector<T> function_values(number_of_population_members_); auto tempX = population_x_.begin();
auto tempY = population_y_.begin(); for (auto &k : function_values) {
k = function_(*( tempX++ ), *( tempY++ ));
}
Sort(function_values, population_x_, population_y_); // Сортировка Хоара в классе
auto amount_of_best_values = static_cast<int>(function_values.size() * percent_of_best_ones_to_live_); return {vector<T>(population_x_.begin(), population_x_.begin() + amount_of_best_values),
vector<T>(population_y_.begin(), population_y_.begin() + amount_of_best_values)};
}
7 Эти и другие мат. функции можно найти здесь: https://ru.wikipedia.org/wiki/Тестовые_функции_для_оптимизации

// Мутация популяций void mutate() {
auto minimal_population_x = *std::min(population_x_.begin(), population_x_.end()); auto minimal_population_y = *std::min(population_y_.begin(), population_y_.end());
std::normal_distribution<> normal_dist {0, min(probability_ * 1000, 0.001)}; // нормальное распределение
for (auto &elem : population_x_) {
elem += minimal_population_x * normal_dist(random_gen_);
}
for (auto &elem : population_y_) {
elem += minimal_population_y * normal_dist(random_gen_);
}
}
//Рекомбинация (размножение) void crossover() {
int population_x_length = population_x_.size(); std::uniform_int_distribution<>
uniform_dist(0, population_x_length - 1); // Равномерное дискретное распределение population_x_.resize(number_of_population_members_); // Увеличение population_y_.resize(number_of_population_members_); // Увеличение
for (int i = population_x_length; i < number_of_population_members_; ++i) { population_x_[i] =
( population_x_[uniform_dist(random_gen_)] + population_x_[uniform_dist(random_gen_)] ) / 2.0; population_y_[i] =
( population_y_[uniform_dist(random_gen_)] + population_y_[uniform_dist(random_gen_)] ) / 2.0;
}
}
//Поиск минимума функции (количество итераций в аргументах)
T searchMinimum(int iterations) { generateInitialPopulation();
for (int i = 0; i < iterations; ++i) {
auto temp_population = getBestMembers(); population_x_ = temp_population.first; population_y_ = temp_population.second; crossover();
mutate();
}
auto minimumValueIndex = getMinimalValueIndex();
return function_(population_x_[minimumValueIndex], population_y_[minimumValueIndex]);
}
//Получение индекса элемента с минимальным значением функции f(x, y) int getMinimalValueIndex() {
vector<T> function_values(number_of_population_members_);
auto tempX = population_x_.begin(), tempY = population_y_.begin(); for (auto &k : function_values) {
k = function_(*( tempX++ ), *( tempY++ ));
}
return std::min(function_values.begin(), function_values.end()) - function_values.begin();
}
//Получение X и Y координаты минимума
pair<T, T> getArgumentsOfMinimumValue() {
auto minimum_value_index = getMinimalValueIndex();
return {population_x_[minimum_value_index], population_y_[minimum_value_index]};
}
GeneticAlgorithm(const GeneticAlgorithm &arg) = delete;
GeneticAlgorithm &operator=(const GeneticAlgorithm &arg) = delete;
GeneticAlgorithm &operator=(GeneticAlgorithm &arg) = delete;
GeneticAlgorithm(GeneticAlgorithm &&arg) = delete;
private:
int number_of_population_members_; // Количество популяций
double percent_of_best_ones_to_live_; // Процент выживаемости (лучшие выживают, остальные погибают) pair<T, T> section_; // Ограничения областей определения
std::function<T(T, T)> function_; // Функция, которую необходимо минимизировать double probability_; // Точность
vector<T> population_x_; // Популяция X vector<T> population_y_; // Популяция Y
std::mt19937 random_gen_; // Генератор рандомных чисел
// Итеративная быстрая сортировка Хоара для трехмерного массива по первому вектору functionValues static void Sort(vector<T> &functionValues, vector<T> &populationX, vector<T> &populationY) {
int Left = 0, Right = functionValues.size() - 1, L2, R2; T PivotValue, Temp;
std::stack<T> Lows, Highs;

Lows.push(Left);
Highs.push(Right); while (!Lows.empty()) {
Left = Lows.top(); Lows.pop();
Right = Highs.top(); Highs.pop();
L2 = Left;
R2 = Right;
PivotValue = functionValues[( Left + Right ) / 2]; do {
while (functionValues[L2] < PivotValue) { ++L2; } while (functionValues[R2] > PivotValue) { --R2; } if (L2 <= R2) {
if (functionValues[L2] > functionValues[R2]) { std::swap(functionValues[L2], functionValues[R2]); std::swap(populationX[L2], populationX[R2]); std::swap(populationY[L2], populationY[R2]);
}
++L2;
if (R2 > 0) { --R2;
}
}
} while (L2 <= R2); if (L2 < Right) {
Lows.push(L2); Highs.push(Right);
}
if (R2 > Left) { Lows.push(Left); Highs.push(R2);
}
}
}
};
// Функция Экли
double AckleyFunction(double x, double y) {
return -20 * exp(-0.2 * sqrt(0.5 * ( x * x + y * y ))) - exp(0.5 * ( cos(2 * M_PI * x) + cos(2 * M_PI * y) )) + M_E + 20;
}
// Функция Била
double BealFunction(double x, double y) {
return pow(1.5 - x + x * y, 2) + pow(2.25 - x + x * y * y, 2) + pow(2.625 - x + x * y * y * y, 2);
}
// Функция Изома
double IzomFunction(double x, double y) {
return -cos(x) * cos(y) * exp(-pow(x - M_PI, 2) - pow(y - M_PI, 2));
}
// Функция Розенброка
double RosenbrokFunction(double x, double y) {
return ( 1.0 - x ) * ( 1.0 - x ) + 100.0 * ( y - x * x ) * ( y - x * x );
}
// Функция Шаффера-N2
double ShafferN2Function(double x, double y) {
return 0.5 + (pow(sin(x * x - y * y), 2) - 0.5) / pow(1 + 0.001 * (x * x + y * y), 2);
}
int main() {
cout << setprecision(16); const double EPS = 1e-7;
int numberOfPopulationMembers = 10000; int iterations = 10000;
double percentOfBestOnesToLive = 0.8; pair<double, double> searchingSection = {-1, 4}; GeneticAlgorithm<double>
GA_A(numberOfPopulationMembers, percentOfBestOnesToLive, searchingSection, AckleyFunction, EPS);
{
cout << "Ackley Function" << endl;
auto minimumValue = GA_A.searchMinimum(iterations); auto minimumPoint = GA_A.getArgumentsOfMinimumValue();
cout << "Minimum: f(" << minimumPoint.first << ", " << minimumPoint.second << ") = " << minimumValue << endl;
cout << "Real: f(0, 0) = 0" << endl << endl;
