-
Перестановка одноименных кванторов.
-
Переименование связанной переменной.
Заменяя связанную переменную формулы
другой переменной, не входящей в эту
формулу, всюду в области действия
квантора, мы получим равносильную
формулу.
16. ИП — исчисление предикатов. Алфавит ИП. Формулы в ИП. Равносильность формул ИП. Приведённые и нормальные формулы ИП. Теоремы о приведённой и нормальной форме формул ИП
Исчисление высказываний — очень узкая логическая система. Есть такие типы логических рассуждений, которые не могут быть осуществлены в рамках этой теории, например: «всякий друг Ивана есть друг Петра. Сидор не есть друг Петра. Следовательно, Сидор не есть друг Ивана». Корректность этих умозаключений основана на внутренней структуре самих предложений и на смысле слов «всякий» и «существуют».
Исчисление предикатов — исчисление функций нескольких переменных, которые в области задания этих переменных могут принимать лишь два значения 1 или 0 (которые мы, как всегда, можем рассматривать как истину или ложь).
-
Алфавит: латинские буквы (возможно с индексами): заглавные для обозначения предикатов, строчные — для обозначения переменных в предикатах.
-
Формулы:
-
Первичные (атомарные) формулы — предикаты. Связки 1-го порядка:
,
и
.
Связки 2-го порядка:
,
,
и
. -
Если
формула, то
— тоже формула (причём все не связанные
кванторами переменные остаются
свободными, все связанные — связанными).
Кроме того, если
формула и
— свободная переменная, входящая в
,
то выражения
и
— тоже формулы, причем
становится связанной. -
Если
и
— две формулы, то
,
,
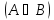и
— также являются формулами, причём
все связанные переменные остаются
связанными, а свободные — свободными. -
Любая формула в ИП получается из первичных с помощью применения конечного числа правил 2 и 3.
Формулы
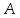и
называются равносильными в
данной интерпретации, если при любых
возможных значениях свободных переменных
(из данной интерпретации) обе формулы
принимают одинаковые значения.
Если
— интерпретация всех предикатов,
входящих в формулы
и
,
то равносильность этих формул в
обозначается
.
Формулы
и
называются равносильными (в ИП),
если они равносильны в любой возможной
интерпретации. Тогда равносильность
обозначается так:
.
Длина
формулы в ИП — общее число входящих
в неё символов предикатов, логических
символов и символов кванторов. Так
формула:
— имеет длину 5 (пять знаков:
).
Приведённая
формула — формула, в
которой из логических символов имеются
только символы конъюнкции
,
дизъюнкции
и отрицания
,
причём отрицание встречается лишь
перед символом предиката.
Нормальная формула — формула, в которой все кванторы стоят в начале или отсутствуют.
Теорема (о существовании равносильной приведённой формулы для любой формулы). Для любой формулы в ИП существует равносильная ей приведённая формула, причём множества свободных и связанных переменных этих двух формул совпадают.
Теорема (о существовании равносильной нормальной формулы для любой приведённой). Для любой приведённой формулы существует равносильная ей нормальная формула, причём длины обоих формул совпадают.
Из этих двух теорем сразу же следует общая теорема.
Теорема (о существовании равносильной приведённой нормальной формулы для любой формулы). Для любой формулы в ИП существует равносильная ей приведённая нормальная формула.