15. Предикаты. Кванторы. Свойства кванторов

Предикат — функция нескольких переменных, которая в области задания этих переменных, может принимать лишь два значения 1 или 0 (которые мы можем рассматривать как истину или ложь). Обозначается заглавными латинскими буквами, а участвующие в нем переменные — строчными латинскими буквами.

Пример предиката: — двуместный предикат.

Предикат может иметь верхний индекс, который обозначает количество аргументов, и нижний для различения букв с одним и тем же числом аргументов. .

Если предикат зависит от переменных, то он называется -местным.

Предикатом также является сама переменная в случае, если она принимает только два значения 1 и 0. В этом случае предикат считается нульместным.

Высказывания — это нульместные предикаты.

Область определения предиката называется интерпретацией.

Например, предложение «(конкретный) студент Иванов имеет дома компьютер» является высказыванием или нульместным предикатом. Это высказывание может принять значение 1 или 0. Однако предложение «студент имеет дома компьютер» уже не является высказыванием, а является одноместным предикатом. Область определения такого предиката — студенты (либо все, либо данного города, ВУЗа или группы).

Квантор — логическая операция, ограничивающая область истинности какого-либо предиката и создающая высказывание.

Особенность предикатов состоит в возможности введения для них кванторов существования 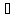и всеобщности .

Пусть — интерпретация предиката . Высказывания:

истинно, если для всех .

истинно, если для хотя бы одного .

(без квантора) содержит свободную переменную .

(с квантором) содержит связанную переменную .

Более сложный пример: .

В данном случае — связанные, а — свободные.

Причём — не является формулой, так как и не могут быть связанными и свободными одновременно (кванторы примыкают к первому предикату; можно исправить ситуацию, добавив скобки ).

Формулы, в которых нет свободных переменных, называются замкнутыми, а формулы, содержащие свободные переменные, — открытыми.

Свойства кванторов:

1. Перенос квантора через отрицание.

Докажем первую равносильность. Пусть — набор всех свободных переменных формулы , отличных от 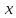, — любой набор значений свободных переменных, — произвольная интерпретация. Возможны два случая:

• Для любого элемента . Тогда для любого элемента . Отсюда по определению: . С другой стороны, в этом случае . Отсюда .

• Для некоторого элемента . Тогда для элемента . Отсюда . С другой стороны, в этом случае . Отсюда .

Докажем вторую равносильность. Применим первую равносильность к формуле . Тогда и, кроме того, .

2. Вынос квантора за скобки.

Пусть формула содержит свободную переменную , а формула не содержит . Тогда имеют место следующие 4 формулы:

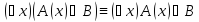
Если формула также зависит от , то будут выполняться только две равносильности:

Докажем первую из этих равносильностей (остальные доказываются аналогично).

Пусть — набор всех свободных переменных формулы . Тогда они же и все свободные переменные формулы .

Рассмотрим произвольную интерпретацию , пусть — любой набор значений свободных переменных . Так как формула не содержит переменной , то можно определить значение этой формулы на наборе (точнее, на его части, относящейся к свободным переменным формулы ). Если , то , и для любого элемента на наборе значений своих свободных переменных формула принимает значение 0. Отсюда . Если , то для любого элемента на наборе формулы и принимают одинаковые истинные значения. Отсюда .