
- •По математической логике и теории алгоритмов
- •1. Определение формальной аксиоматической теории (фат). Секвенции (выводы). Формулы. Построение формул. 5 свойств выводов
- •2. Исчисление высказываний. Построение ив как фат. Алфавит, формулы, аксиомы, выводы и правила вывода
- •3. Доказать, исходя из аксиом ив и правила вывода секвенцию — первое свойство выводов ив
- •4. Доказать, исходя из свойств выводов, аксиом ив и правила вывода ив следующие свойства выводов ив
- •Если , то .
- •Если и , то .
- •Если и — любая формула ив, то .
- •5. Теорема дедукции
- •6. Свойство транзитивности импликации. Доказать секвенцию: ,
- •7. Противоречивые формулы
- •Если , то .
- •8. Обоснование доказательства от противного: доказать, что если , то
- •9. Тождественность формул ив. Доказать тождество:
- •10. Аксиоматическое введение в ив и
- •11. Теорема о том, что всякая выводимая в ив формула есть тавтология
- •12. Доказательство леммы
- •13. Теорема о том, что любая тавтология выводима в ив
- •14. Полнота и непротиворечивость ив
- •15. Предикаты. Кванторы. Свойства кванторов
- •Перенос квантора через отрицание.
- •Вынос квантора за скобки.
- •Перестановка одноименных кванторов.
- •Переименование связанной переменной.
- •17. Выполнимость и общезначимость формул ип. Общезначимость формул , .
- •18. Аксиомы ип. Общезначимость аксиом ип. Правила вывода ип. Оформление ип как фат
- •19. Теорема об общезначимости формул ип, получающихся из общезначимых по любому из 4-х правил вывода ип
- •20. Полнота и непротиворечивость ип. Теорема Гёделя. Тезис Чёрча
- •21. Алгоритмы. Определение (интуитивное) алгоритма. Свойства алгоритмов. Направления поисков точного определения алгоритма. Вычислимые функции. Проблема алгоритмической неразрешимости
- •22. Рекурсивные функции. 3 простейших прф (примитивно-рекурсивных функций). Оператор суперпозиции. Примеры
- •23. Оператор пр (примитивной рекурсии). Доказать, что функции , , , , — прф
- •24. Оператор минимизации. Частично-рекурсивные функции. Доказать, что — чрф. Точное определение алгоритма. Тезис Чёрча
- •25. Машина Тьюринга. Тьюринговая функциональная схема. Точное определение алгоритма. Тезис Тьюринга
- •26. Функции, вычислимые по Тьюрингу. Доказать, что 3 простейших прф — вычислимы по Тьюрингу
- •27. Геделева нумерация мт. Примеры: по номеру найти мт и по мт записать номер
- •28. Самоприменимость мт. Теорема об алгоритмической неразрешимости проблемы самоприменимости
- •29. Нормальные алгоритмы Маркова. Точное определение алгоритма. Примеры
- •Литература
11. Теорема о том, что всякая выводимая в ив формула есть тавтология
Тавтология — тождественно истинное высказывание.
Теорема.
Если формула
 выводима, то она тождественно истинна
/ является тавтологией (то есть на любом
наборе переменных принимает значение,
равное 1).
выводима, то она тождественно истинна
/ является тавтологией (то есть на любом
наборе переменных принимает значение,
равное 1).
Доказательство.
[Для доказательства этой теоремы нужна лемма 12-го вопроса!]
Пусть
формула
 выводима (из аксиом). Докажем, что при
любых значениях переменных, входящих
в неё, формула
выводима (из аксиом). Докажем, что при
любых значениях переменных, входящих
в неё, формула
 принимает значение 1. Непосредственно
проверяем, что все аксиомы являются
тождественно истинными формулами. Так
как импликация из истины выводит только
истину, то по правилу вывода
принимает значение 1. Непосредственно
проверяем, что все аксиомы являются
тождественно истинными формулами. Так
как импликация из истины выводит только
истину, то по правилу вывода
 (
( )
получаем, что
)
получаем, что
 тоже истинна. Так как других правил
вывода в ИВ нет, то все выводимые (из
аксиом) формулы тождественно истинны.
тоже истинна. Так как других правил
вывода в ИВ нет, то все выводимые (из
аксиом) формулы тождественно истинны.
12. Доказательство леммы
Исчисление высказываний — чисто логический вывод одних суждений из других. Ранее такая наука называлась схоластикой. То есть из некоторых общепризнанных фактов выводились другие суждения без всяких опытов. Например, если человек идёт в кино, то у него должны быть деньги. Разумеется, этот пример является простым и его легко провести в жизни без всякой дискретной математики. Однако в других случаях формальный логический вывод без применения правил ИВ бывает очень сложным и применение этой теории становится обязательным. Поэтому, для получения логических выводов мы заменяем суждения (которые могут быть либо истинными, либо ложными) латинскими буквами и получаем первичные формулы ИВ (и тем самым отказываемся от смысла этих суждений) и тогда мы можем считать, что эти самые буквы (то есть переменные или первичные формулы) являются числами, которые могут принимать только два значения 0 и 1.
Так
как в формулы ИВ кроме переменных (то
есть первичных формул) входят связки
(отрицание и импликация), то по правилам
этих булевых функций любая формула на
определенном наборе переменных также
принимает значения 0 или 1. Таким образом,
если
 — формула в ИВ,
— формула в ИВ,
 — набор её переменных и
— набор её переменных и
 — любой набор возможных значений этих
переменных (из нулей и единиц), то
— любой набор возможных значений этих
переменных (из нулей и единиц), то
 — значение формулы
— значение формулы
 на этом наборе. Тем самым мы получаем
одну из возможных интерпретаций теории
ИВ, которая переводит схоластические
рассуждения на язык чисел (нулей и
единиц).
на этом наборе. Тем самым мы получаем
одну из возможных интерпретаций теории
ИВ, которая переводит схоластические
рассуждения на язык чисел (нулей и
единиц).
Пусть
 .
Таким образом, при любом конкретном
.
Таким образом, при любом конкретном
 выражение
выражение
 является формулой в ИВ.
является формулой в ИВ.
Пример.


Формула
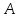 выводима, если она выводится из аксиом
(то есть
выводима, если она выводится из аксиом
(то есть
 ).
).
Пусть
длина формулы
 означает количество связок в ней (то
есть символов
означает количество связок в ней (то
есть символов
 и
и
 ).
).
Лемма.
Пусть
 — формула в ИВ,
— формула в ИВ,
 — набор её переменных и
— набор её переменных и
 — любой набор возможных значений
этих переменных (из нулей и единиц) и
— любой набор возможных значений
этих переменных (из нулей и единиц) и
 — значение формулы
— значение формулы
 на этом наборе. Тогда верна следующая
секвенция:
на этом наборе. Тогда верна следующая
секвенция:

Доказательство
этой леммы проведём индукцией по длине
формулы
 ,
которую обозначим
,
которую обозначим
 (к). При
(к). При
 формула
формула
 не содержит символов отрицания и
импликации и состоит из одной переменной
не содержит символов отрицания и
импликации и состоит из одной переменной
 .
Поэтому в этом случае доказательство
леммы сводится к очевидной секвенции
.
Поэтому в этом случае доказательство
леммы сводится к очевидной секвенции
 .
.
Пусть
 и пусть формула (1) верна для всех формул,
длина которых строго меньше
и пусть формула (1) верна для всех формул,
длина которых строго меньше
 .
Докажем тогда, что лемма верна для
формулы
.
Докажем тогда, что лемма верна для
формулы
 .
.
СЛУЧАЙ
1. Предположим, что формула
 совпадает с формулой
совпадает с формулой
 (
( ).
Тогда длина
).
Тогда длина
 равна
равна
 ,
и для
,
и для
 лемма верна по индукционному
предположению. Кроме того,
в формулы
лемма верна по индукционному
предположению. Кроме того,
в формулы
 и
и
 входят одни и те же переменные. Пусть
для набора
входят одни и те же переменные. Пусть
для набора
 значение формулы
значение формулы
 на этом наборе равно
на этом наборе равно
 ,
а формулы
,
а формулы
 равно
равно
 (так как
(так как
 ,
то очевидно, что
,
то очевидно, что
 ).
).
а)
Пусть
 ,
тогда
,
тогда
 .
По индукционному предположению верна
секвенция
.
По индукционному предположению верна
секвенция
 .
Так как
.
Так как
 и
и
 ,
то
,
то
 ,
то есть лемма верна:
,
то есть лемма верна:

б)
Пусть ,
тогда
,
тогда
 .
По индукционному предположению верна
секвенция
.
По индукционному предположению верна
секвенция
 .
Так как
.
Так как
 и
и
 ,
то
,
то
 ,
то есть лемма верна:
,
то есть лемма верна:

СЛУЧАЙ
2. Предположим, что формула
 имеет вид
имеет вид
 (
( ).
Длина формул
).
Длина формул
 и
и
 меньше
меньше
 ,
поэтому для обеих формул лемма верна
по индукционному предположению (в
формулы
,
поэтому для обеих формул лемма верна
по индукционному предположению (в
формулы
 и
и
 может входить меньшее число переменных,
но так как лишние формулы не мешают, то
лемма будет верна). Пусть для данного
набора
может входить меньшее число переменных,
но так как лишние формулы не мешают, то
лемма будет верна). Пусть для данного
набора
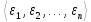 значения
значения
 ,
,
 ,
,
 являются значениями формул
являются значениями формул
 ,
,
 и
и
 соответственно.
соответственно.
а)
Пусть
 ,
тогда
,
тогда
 .
По индуктивному предположению верно:
.
По индуктивному предположению верно:


По
уже доказанному в 7-ом вопросе утверждению
(«если
 ,
то
,
то
 »)
и уже доказанному в 9-ом вопросе утверждению
(«
»)
и уже доказанному в 9-ом вопросе утверждению
(« »)
— переносим
»)
— переносим
 влево:
влево:

По
свойству №3 («лишняя формула не мешает»)
— добавляем
 :
:

По
уже доказанному в 8-ом вопросе утверждению
(«если
 ,
то
,
то
 »):
»):

По
теореме дедукции («если
 ,
то
,
то
 »):
»):

Следовательно,
 !
!
б)
Пусть
 ,
тогда
,
тогда
 и
и
 .
По индуктивному предположению
верно:
.
По индуктивному предположению
верно:
 (1)
(1)


По
уже доказанному в 7-ом вопросе утверждению
(«если
 ,
то
,
то
 »)
и уже доказанному в 9-ом вопросе утверждению
(«
»)
и уже доказанному в 9-ом вопросе утверждению
(« »)
— переносим
»)
— переносим
 влево:
влево:

По
свойству №2 («порядок формул не имеет
значения») и уже доказанному в 8-ом
вопросе утверждению («если
 ,
то
,
то
 »)
— переносим
»)
— переносим
 вправо:
вправо:

По
свойству №3 («лишняя формула не
мешает») и по свойству №2
(«порядок формул не имеет значения»)
— добавляем
 в начало:
в начало:

По
свойству №4 («удаление выводимой
формулы») — так как
 и
и
 ,
то можно убрать формулы
,
то можно убрать формулы
 и
и
 как выводимые:
как выводимые:


в)
Пусть
 ,
тогда
,
тогда
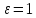 и
и
 .
По индуктивному предположению верно:
.
По индуктивному предположению верно:

По
свойству №1 (« !»
или «
!»
или « !»):
!»):

По
свойству №3 («лишняя формула не
мешает») и по свойству №2
(«порядок формул не имеет значения»)
— добавляем
 в начало:
в начало:

По теореме дедукции («если
 ,
то
,
то
 »):
»):

По
свойству №3 («лишняя формула не
мешает») и по свойству №2
(«порядок формул не имеет значения»)
— добавляем
 в начало:
в начало:

По
свойству №4 («удаление выводимой
формулы») — так как
 ,
то можно убрать формулу
,
то можно убрать формулу
 как выводимую:
как выводимую:


Лемма доказана.
