7. Противоречивые формулы
Доказать:
-
Если
и
,
то
(«из ложного следует всё, что угодно»).
Пусть
— любая формула. Тогда из двух данных
секвенций по свойству ИВ №4 («если
и
— любая формула ИВ, то
»)
следует, что
и
.
По аксиоме А3 (заметим, что аксиома
следует из любых формул):
По свойству №3 («лишняя
формула не мешает») — добавляем
:
Тогда применяя 2 раза свойство ИВ №2
(«если
,
то
»),
получим:
По свойству №4 («удаление выводимой
формулы») — так как
и
,
то выводимые формулы
и
можно убрать:
-
Если , то .
По условию:
По свойству №3 («лишняя
формула не мешает») — добавляем
:
Следующее утверждение также
справедливо, так как по свойству №1 (
)
и по свойству №3 («лишняя формула
не мешает») — добавляем
:
По уже доказанному выше
утверждению («если
и
,
то
»)
— так как
и
,
то получим:
8. Обоснование доказательства от противного: доказать, что если , то
Доказательство «от противного» — вид доказательства, при котором «доказывание» некоторого суждения (тезиса доказательства) осуществляется через опровержение отрицания этого суждения — антитезиса.
Доказательство
утверждения
проводится следующим образом. Сначала
принимают предположение, что утверждение
неверно, а затем доказывают, что при
таком предположении было бы верно
некоторое утверждение
,
которое заведомо неверно.
Из
определения импликации следует, что,
если
ложно, то формула
истинна тогда и только тогда, когда
ложно, следовательно утверждение
истинно.
Полученное
противоречие показывает, что исходное
предположение было неверным, и поэтому
верно утверждение
,
которое по закону двойного отрицания
равносильно утверждению
.
Доказательство №1 (если
,
то
).
Так
как
,
то есть из
и
выводима любая формула, то, в частности,
выводима и формула
:
.
Значит,
по теореме дедукции.
По
свойству ИВ №1 (
)
из любых формул (в частности, из формул
)
выводится
,
а по свойству №3: «лишняя формула не
мешает»:
.
С другой стороны, по аксиоме А3:
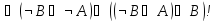
Имеем
(
,
свойство №3: «лишняя формула не мешает»
— добавляем
):
Применяя
2 раза свойство ИВ №2 («если
,
то
»),
получим:
По
свойству №4 («удаление выводимой
формулы») — так как
и
,
то, удаляя выводимые формулы
и
,
получим:
!
Доказательство №2 (если
,
то
).
В
самом начале докажем, что если
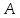— любая формула, то
.
По
свойству №1 (
):
По
свойству №3 («лишняя формула не мешает»)
— добавляем
:
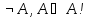
Следующее
утверждение также справедливо, так как
по свойству №1 (
)
и по свойству №3 («лишняя формула не
мешает») — добавляем
:
То
есть
и
— по уже доказанному в 7-ом вопросе
утверждению («если
и
,
то
»)
и свойству №2 («порядок формул не имеет
значения»):
Теперь
перейдём к основному доказательству
(«если
,
то
»).
Так
как по доказанному выше («если
— любая формула, то
»)
и свойству №2 («порядок формул не имеет
значения»), то имеем:
Так
как по доказательству №1 («если
,
то
»),
то:
Кроме
того, формулы
и
по условию противоречивы (
).
Тогда по свойству №3 («лишняя формула
не мешает») — будут противоречивы 3
формулы:
Как
уже было написано,
— значит по свойству №4 («удаление
выводимой формулы») можно удалить
выводимую формулу
:
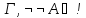
Тогда
по доказательству №1 («если
,
то
»)
получаем
.
Вывод.
Таким образом, эти
два свойства означают, что любую из
противоречивых формул можно переносить
за знак вывода
.