29. Нормальные алгоритмы Маркова. Точное определение алгоритма. Примеры

Будем называть алфавитом всякое непустое конечное множество символов, а сами символы алфавита будем называть буквами.

Слово в алфавите — всякая конечная последовательность букв алфавита .

Пустая последовательность букв называется пустым словом и обозначается .

Если обозначает слово и обозначает слово , то обозначает объединение . В частности, ; кроме того, .

Принято говорить, что слово входит в слово , если существуют такие (возможно, пустые) слова и , что .

Алфавит называется расширением алфавита , если . Очевидно, что в этом случае всякое слово в алфавите является также словом в алфавите .

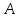Алгоритмом в алфавите называется вычислимая функция, областью определения которой служит какое-нибудь подмножество множества всех слов в алфавите и значениями которой являются также слова из . Если , то есть — расширение , то всякий алгоритм в называется алгоритмом над алфавитом .

Пусть есть слово в алфавите ; говорят, что алгоритм применим к слову , если содержится в области определения .

Большинство известных алгоритмов можно разбить на некоторые простейшие шаги (одно из свойств алгоритма — элементарность каждого шага). Следуя А. А. Маркову, в качестве элементарной операции, на базе которой строятся алгоритмы, выделим подстановку одного слова вместо другого.

Если и — слова в алфавите , то выражение называется простой формулой подстановки в , а называется заключительной формулой подстановки в ; при этом предполагается, что символы стрелка «» и точка «» не являются буквами алфавита , а каждое слово и может быть и пустым словом.

Пусть обозначает одну из формул подстановки или .

Конечный список формул подстановки в алфавите :

Называется схемой алгоритма и порождает следующий алгоритм в алфавите , называемый алгоритмом Маркова или нормальным алгоритмом.

Пусть — слово в алфавите . Здесь может быть одно из двух:

1. Ни одно из слов не входит в слово (обозначается: ).

2. Среди слов существуют такие, которые входят в . Пусть — наименьшее целое число из такое, что входит в , и — слово, которое получается, если самое левое вхождение слова в слово заменить словом .

Тот факт, что и находятся в описанном отношении, коротко запишем в виде:

, если — простая подстановка;

, если — заключительная подстановка.

В первом случае говорят, что алгоритм просто переводит слово в слово , а во втором случае говорят, что алгоритм заключительно переводит слово в слово .

Пусть далее означает, что существует такая последовательность слов в алфавите , что для , причем либо , либо (в этом последнем случае вместо пишут ).

Положим теперь тогда и только тогда, когда либо , либо и .

Это и есть точное (строгое) определение алгоритма. Любой алгоритм, если он существует, может быть представлен как нормальный алгоритм Маркова.

Таким образом, работу алгоритма можно описать следующим образом:

Пусть дано слово в алфавите . Находим первую в схеме алгоритма формулу подстановки такую, что входит в . Совершаем подстановку слова вместо самого левого вхождения слова в . Пусть — результат такой подстановки. Если , то работа этой подстановки заканчивается и далее переходим к следующей подстановке, такой, что входит в (то есть к -той подстановке), и так же совершаем подстановку , результат которой и так далее. Если же , то применяем к тот же поиск, который был только что применён к (до тех пор, пока входит в ) и так далее.

Если на конечном этапе будет получено такое слово , что : , то есть ни одно из слов не входит в , то работа алгоритма заканчивается, и будет его значением. Если же описанный процесс на конечном этапе не заканчивается, то говорят, что алгоритм неприменим к данному слову .

Примеры.

1. Пусть схема алгоритма: .

Тогда, если начальное слово , то алгоритм работает так:

Обратим внимание на то, что произошло потому, что заключительной подстановки в схеме алгоритма нет. Закончиться алгоритм может, как уже было написано ранее, либо при последней заключительной подстановке , либо при простой подстановке при отсутствии зацикливания ().

2. Пусть схема алгоритма: .

Тогда, если начальное слово , то алгоритм работает так:

3. Пусть схема алгоритма: .

Тогда, если начальное слово , то алгоритм работает так:

4. Пусть схема алгоритма: .

Тогда, если начальное слово , то алгоритм работает так:

Так как подстановка — простая, то алгоритм не заканчивается, процесс продолжается бесконечно, значит данный алгоритм неприменим к данному слову.

Пример 1. Пусть есть алфавит . Рассмотрим схему . Определяемый этой схемой нормальный алгоритм перерабатывает всякое слово в алфавите , содержащее хотя бы одно вхождение буквы , в слово, которое получается вычёркиванием в самого левого вхождения буквы .

Если , то , где 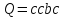. Данный алгоритм неприменим к пустым словам, не содержащим буквы , так как простые подстановки будут перерабатывать эти слова в себя самих, но тогда всегда , и мы не приходим к заключительной подстановке, то есть процесс будет продолжаться бесконечно.

Если же рассмотреть несколько изменённую схему , то алгоритм применительно к слову 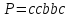сработает так: .

Пример 2. Пусть есть алфавит . Рассмотрим схему: . Эта схема определяет нормальный алгоритм , перерабатывающий всякое слово в алфавите в пустое слово.

Например, .

Вопрос о неразрешимости алгоритмических массовых проблем с точки зрения определения нормального алгоритма Маркова можно поставить так: если не существует нормального алгоритма Маркова, решающего данную массовую проблему, то данная массовая проблема алгоритмически неразрешима.

В частности, американский математик Чёрч в 1936 г. доказал одну из первых теорем такого рода:

Теорема Чёрча. Проблема распознавания выводимости алгоритмически неразрешима.

Проблема распознавания выводимости: для любых двух формул и в логическом исчислении узнать, существует ли дедуктивная цепочка, ведущая от к , или нет. Решение этой проблемы понимается в смысле вопроса о существовании алгоритма, дающего ответ при любых и .