28. Самоприменимость мт. Теорема об алгоритмической неразрешимости проблемы самоприменимости

Как и раньше, кодируем натуральные числа символом 1. Будем рассматривать МТ, алфавит которых содержит символ 1.

МТ называется применимой к начальному слову, если она, начав работать с этим словом на ленте, придёт в заключительное состояние.

МТ называется самоприменимой, если она применима к своему номеру , то есть если она начинает свою работу со своим кодом (то есть по программе, восстановленной по этому коду) и заканчивает работу, то есть останавливается в какой-то конфигурации, то есть перерабатывает код в какое-то слово.

Пример тьюринговой функциональной схемы самоприменимой машины:

	0	1

Данная машина работает так: к любому слову, состоящему из символов 1, она прибавляет ещё один символ 1 справа и останавливается.

Очевидный пример несамоприменимой машины — если в правых частях команд не встречается — стоп-состояние. Такая машина неприменима ни к какому слову.

Рассмотрим алгоритмическую проблему самоприменимости, то есть существует ли алгоритм, который по любому устанавливает, самоприменима ли она или нет. Согласно Тьюрингу, это означает, существует ли такая МТ, которая была бы применима к кодам номеров всех МТ и в зависимости от того, самоприменима МТ или нет, имела бы различные заключительные конфигурации. Например, в случае самоприменимости МТ заключительная конфигурация имела бы вид , а в случае несамоприменимости — .

Теорема. Проблема самоприменимости алгоритмически неразрешима, то есть не существует МТ, решающей эту проблему в указанном выше смысле.

Доказательство.

Предположим противное, что такая машина существует (например, в номер самоприменимой машины перерабатывается в 1, а несамоприменимой в 0). Тогда можно построить машину , которая:

1. Применима ко всем кодам номеров несамоприменимых машин (то есть по номеру устанавливает, что машина несамоприменима).

2. Неприменима ко всем кодам номеров самоприменимых машин.

Действительно, машина получается из следующим образом: алфавит сохраняется неизменным, заключительное состояние машины считается не заключительным состоянием машины , а заключительным состоянием считается новое состояние , причём программа состоит из всех команд и ещё двух команд:

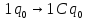(«зацикливание»)

Очевидно, что удовлетворяет требованиям 1) и 2), так как конфигурация машины означает, что установлена самоприменимость исследуемой МТ, а команда зацикливает программу, что означает, что неприменима к номеру самоприменимой МТ; в то же время заключительная конфигурация машины устанавливает несамоприменимость МТ, а команда означает, что применима к несамоприменимой МТ (не зацикливается).

Итак, если самоприменима (то есть применима к коду своего номера), то она применима и к коду самоприменимой МТ, но тогда требование 2) не удовлетворено; если же несамоприменима (то есть неприменима к коду своего номера), то она неприменима и к коду несамоприменимой МТ, но тогда не выполнено требование 1). Следовательно, мы пришли к противоречию, то есть не существует машины , решающей проблему самоприменимости.

Заметим, что неразрешима именно массовая проблема: не существует единого алгоритма, который решал бы проблему самоприменимости.

Используя результат этой теоремы, можно доказать неразрешимость других алгоритмических проблем. Например, можно доказать следующую теорему.

Теорема. Проблема применимости МТ к начальному слову алгоритмически неразрешима, то есть не существует МТ (а, следовательно, и алгоритма), разрешающей проблему определения по номеру и начальному слову , применима ли МТ к .

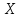Иначе говоря, можно ли построить МТ, которая была бы применима ко всем словам вида (МТ — произвольная машина, — разделитель, — произвольное слово), и в случае, если МТ применима к слову , то заключительная конфигурация имела бы вид , а в случае, если МТ неприменима к слову , заключительная конфигурация имела бы вид .