26. Функции, вычислимые по Тьюрингу. Доказать, что 3 простейших прф — вычислимы по Тьюрингу

Воспользуемся специальным кодированием натуральных чисел в алфавите : каждое число представим символов, то есть числа 0, 1, 2, … кодируем словами

Частичная числовая -местная функция называется вычислимой по Тьюрингу, если существует МТ с алфавитом такая, что при начальной конфигурации, задающей в алфавите МТ значения , МТ начинает работу и, если при таких значениях функция определена, то МТ заканчивает работу в конфигурации, определяющей значение :

Теорема. Функции, вычислимые по Тьюрингу, есть частично-рекурсивные функции, и наоборот.

Докажем, что простейшие ПРФ есть функции, вычислимые по Тьюрингу.

1. для вычисления этой функции задается Тьюринговая схема с двумя состояниями :

	0	1

Посмотрим, как работает эта МТ:

2. для вычисления этой функции задаётся Тьюринговая схема с двумя состояниями :

	0	1

Посмотрим, как работает эта МТ:

В данном случае из 11 (то есть 1) получили 111 (то есть 2) (к слову: 1 – это 0).

3. .

Начальная информация — должны быть заданы .

На ленте в алфавите это группы 1, разделенные одной пустой клеткой, то есть 0.

Если две или более пустых клеток, то слева или справа от них только пустые клетки, то есть они показывают «границы» информации.

Например, конфигурация такая:

То есть заданы значения аргументов функции 4-х переменных — начальная конфигурация. Наша МТ после окончания работы должна выдать значение .

Пусть 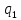— сохранение 1 в , — обнуление 1 у остальных аргументов, — определение границ, то есть конца информации, — стоп-состояние.

В данном случае удобнее, чтобы в начальном состоянии управляющая головка находилась в крайнем левом положении, то есть под первой слева непустой клеткой.

Посмотрим, как работает данная МТ. Пусть начальная конфигурация:

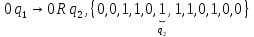
27. Геделева нумерация мт. Примеры: по номеру найти мт и по мт записать номер

Каждая МТ по определению есть набор , где — внешний алфавит с выделенным пустым символом , — внутренний алфавит состояний с выделенными символами конечного () и начального () состояний, — программа, то есть конечная последовательность упорядоченных пятёрок символов (). Существуют некоторые обширные алфавиты и , в которых записываются все упомянутые символы ().

Пусть — последовательность всех простых чисел, расположенных в порядке возрастания, то есть последовательность

Номером МТ называется число:

Естественно, что не все натуральные числа являются номерами каких-то МТ. Но если — номер какой-то МТ в алфавите , , то её программу можно однозначно восстановить по номеру МТ.

Примеры.

1. для вычисления функции , П: , .

Пусть .

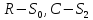Номер этой МТ: .

2. Пусть 

.