25. Машина Тьюринга. Тьюринговая функциональная схема. Точное определение алгоритма. Тезис Тьюринга

Автоматизм, необходимый при реализации алгоритма, естественно привёл к мысли о передаче функции человека, реализующего алгоритм, машине. Эту идею предложили в 30-е годы прошлого века почти одновременно американский математик Эмиль Пост и английский математик Алан Тьюринг.

Рассмотрим один из вариантов, который носит название «машина Тьюринга».

Машина Тьюринга (МТ) — математическая модель идеализированного вычислительного устройства.

Устройство машины Тьюринга включает в себя:

1. Внешний алфавит, то есть конечное множество символов . В этом алфавите в виде слова кодируется та информация, которая подаётся в машину, то есть конечная последовательность символов алфавита. Машину перерабатывает эту информацию в новое слово.

2. Внутренний алфавит машины состоит из символов: . Символы — конечное число состояний машины, то есть возможных реакций МТ на любой символ внешнего алфавита.

Два состояния имеют особое назначение: — начальное состояние машины (в этом состоянии машина начинает работать), — заключительное состояние (стоп-состояние; остановка).

Символы — это символы сдвига на 1 ячейку соответственно влево 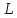, на месте и вправо .

Если нет состояния , то машина не начнёт работу, а если нет состояния , то машина не остановится, то есть зациклится.

3. Бесконечная в обе стороны лента, разбитая на ячейки (клетки). Это — внешняя память машины. В каждую ячейку может быть записан только один символ внешнего алфавита. Не пустым, то есть заполненным, может быть только конечное число клеток. Пустую клетку обозначают символом (иногда, если 0 не является символом алфавита, то вместо пишут 0).

4. Управляющая (считывающая) головка. Она передвигается вдоль ленты и может останавливаться против какой-то клетки, то есть «считывать» символ в этой клетке. За один шаг головка может сдвинуться лишь на одну ячейку влево или на месте или вправо, что обозначается символами соответственно.

Конфигурация на ленте — совокупность, образованная последовательностью символов, записанных во внешней памяти (ленте), внутренним состоянием и номером воспринимаемой ячейки.

К началу работы машины на ленту подаётся начальная информация и управляющая головка, как правило, находится у крайнего правого (или левого) символа всех непустых клеток с указанием начального состояния . Это так называемая начальная конфигурация.

Работа МТ складывается из тактов (шагов).

За один шаг машина может в данной ячейке:

• Написать один символ или оставить прежний в данной ячейке.

• Перейти в новое состояние или остаться в прежнем.

• Сдвинуться по ленте на одну клетку влево (или вправо) или остаться на месте.

В зависимости от того, какая была подана начальная информация , то есть какая была начальная конфигурация, возможны 2 случая:

1. МТ начинает работу (не начать не может, так как при правильном задании должна быть известна реакция МТ на любой символ) и после конечного числа шагов останавливается в некоторой конфигурации, то есть переходит в стоп-состояние . При этом на ленте оказывается изображённой некоторая информация . В этом случае говорят, что МТ применима к информации и перерабатывает её в , то есть существует и работает алгоритм перевода в .

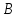2. МТ не останавливается, то есть не переходит в состояние , как говорят, «зацикливается». В таком случае говорят, что данная МТ неприменима к информации .

В каждый момент работы МТ конфигурация записывается следующим образом:

Это означает, что до и после 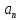ячейки пустые, то есть в них стоят (или 0), а в ячейках могут быть как нулевые, так и ненулевые символы внешнего алфавита . При этом машина находится в состоянии .

Схему работы МТ, то есть алгоритма можно записать как программу МТ, то есть как конечное число шагов (тактов), каждый из которых записывается в виде:

Здесь 5 символов, 2 — из внешнего (), 3 — из внутреннего алфавитов. Такой шаг означает, что символ в ячейке, возле которой стоит управляющая головка, заменяется на символ , МТ из состояния переходит в состояние и при этом головка или сдвигается на 1 клетку влево () или вправо () или остаётся на месте ().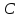

Программу МТ удобно записывать в виде двумерной таблицы, которая называется тьюринговой функциональной схемой.

			…
			…
			…
…	…	….	…	…
			…

Пример. Дана Тьюринговая функциональная схема:

— символ пустой клетки.

Рассмотрим, как по такой программе работает МТ.

Пример 1.

Пусть начальная конфигурация:

, получаем:

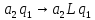, получаем:

, получаем:

, получаем:

То есть МТ переработала слово в слово .

Пример 2.

Пусть начальная конфигурации:

, получаем:

, получаем:

, получаем:

, получаем:

, получаем:

Видим, что пришли ко второй конфигурации, то есть процесс начал повторяться, зацикливаться, то есть делаем вывод, что данная МТ неприменима к слову .

Тезис Тьюринга. Всякий алгоритм может быть задан посредством тьюринговой функциональной схемы и реализован в соответствующей МТ.

Этот тезис, так же, как и тезис Чёрча, нельзя доказать, так как он связывается нестрогое понятие алгоритма со строгим определением МТ. Его можно опровергнуть, если удастся привести пример алгоритма, который не может быть реализован с помощью МТ. Однако все известные до сих пор алгоритмы могут быть заданы посредством МТ.

Понятия рекурсивного алгоритма (алгоритм — это процесс вычисления частично-рекурсивной функции) и машины Тьюринга (алгоритм — то, что может быть задано посредством МТ), а также другие определения алгоритма, такие как машина Поста, нормальные алгоритмы Маркова, нейронные сети Неймана, равносильны.

Строгое определение алгоритма:

Всякий алгоритм — есть процесс вычисления частично-рекурсивной функции.

Если функция не частично-рекурсивная алгоритма для её вычисления нет.