24. Оператор минимизации. Частично-рекурсивные функции. Доказать, что — чрф. Точное определение алгоритма. Тезис Чёрча

ПРФ — примитивно-рекурсивная функция, определена для всех значений аргументов (каждый из аргументов пробегает свои значения независимо от других). Иногда это является недостатком, в том смысле, что вычислимая функция на самом деле не является ПРФ из-за того, что определена не для всех значений аргументов. Напомним, что и аргументы вычислимой функции, и сама функция принимают только неотрицательные целочисленные значения.

Например, естественно считать вычислимой.

Но такие функции не могут быть ПРФ. Поэтому требуется ввести ещё один оператор.

Оператор минимизации (-оператор).

Пусть имеется функция и пусть — фиксированы, тогда возможны 3 случая:

1. При любых : . В этом случае будем считать, что оператор минимизации не определен в точке .

2. . Тогда .

3. Пусть — наименьший корень уравнения (где 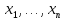— фиксированы). Тогда возможны 2 случая:

   1. и определены, тогда .

   2. Среди есть хотя бы одно неопределённое значение, тогда тоже не определен.

Пишем 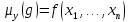, так как очевидно, что оператор зависит от , то есть от точки, в которой мы его считаем.

Оператор минимизации — функция переменных , значение которой равно наименьшему корню уравнения : при условии, что определены значения , то есть значения при , меньших чем .

Для вычисления оператора минимизации есть следующий алгоритм:

1. Вычисляем . Если равно 0, то . Если же не равно 0, то переходим следующему шагу.

2. Вычисляем . Если равно 0, то . Если же не равно 0, то переходим к следующему шагу () и так далее.

Если или на каком-то шаге значение не определено, то считаем неопределенным.

Частично-рекурсивная функция — функция, которая может быть получена с помощью применения конечного числа раз 3-х операторов (суперпозиции, примитивной рекурсии и минимизации) к простейшим ПРФ .

Доказать, что — частично-рекурсивная функция.

Вспомним, что функции и — ПРФ.

Рассмотрим функцию . Эта функция есть ПРФ как сумма двух ПРФ.

Введём теперь функцию . Очевидно, что она ПРФ.

Тогда .

Действительно, уравнение это уравнение .

Если , то корень — наименьший корень этого уравнения, так как:

…

если

Если , то корень .

Если же , то ни при каком , то есть оператор не определен.

Таким образом мы доказали, что получена оператором минимизации из ПРФ, и поэтому является частично-рекурсивной функцией.

Общерекурсивная функция — частично-рекурсивная функция, которая определена при всех возможных значениях аргументов.

Тезис Чёрча. Любая частично-рекурсивная функция является вычислимой, то есть существует алгоритм для её вычисления, и, наоборот, любая вычислимая функция есть частично-рекурсивная функция.

Этот тезис нельзя доказать, так как он связывает строгое математическое понятие частично-рекурсивной функции с нестрогим математическим понятием вычислимой функции, но его можно опровергнуть, если построить пример функции вычислимой, но не являющейся частично-рекурсивной. Однако, до сих пор такой функции не найдено.

Первое строгое определение алгоритма:

Всякий алгоритм — есть процесс вычисления частично-рекурсивной функции.

Если функция не частично-рекурсивная алгоритма для её вычисления нет.