Экзаменационные вопросы © Kovalenko Leonid

По математической логике и теории алгоритмов

Весь материал взят с книг и научных работ. Ничего не придумано☺

1. Определение формальной аксиоматической теории (ФАТ). Секвенции (выводы). Формулы. Построение формул. 5 свойств выводов 3

2. Исчисление высказываний. Построение ИВ как ФАТ. Алфавит, формулы, аксиомы, выводы и правила вывода 4

3. Доказать, исходя из аксиом ИВ и правила вывода секвенцию — первое свойство выводов ИВ 5

4. Доказать, исходя из свойств выводов, аксиом ИВ и правила вывода ИВ следующие свойства выводов ИВ 6

5. Теорема дедукции 6

6. Свойство транзитивности импликации. Доказать секвенцию: , 8

7. Противоречивые формулы 9

8. Обоснование доказательства от противного: доказать, что если , то 10

9. Тождественность формул ИВ. Доказать тождество: 11

10. Аксиоматическое введение в ИВ и 13

11. Теорема о том, что всякая выводимая в ИВ формула есть тавтология 13

12. Доказательство леммы 13

13. Теорема о том, что любая тавтология выводима в ИВ 16

14. Полнота и непротиворечивость ИВ 17

15. Предикаты. Кванторы. Свойства кванторов 18

16. ИП — исчисление предикатов. Алфавит ИП. Формулы в ИП. Равносильность формул ИП. Приведённые и нормальные формулы ИП. Теоремы о приведённой и нормальной форме формул ИП 20

17. Выполнимость и общезначимость формул ИП. Общезначимость формул , . 22

18. Аксиомы ИП. Общезначимость аксиом ИП. Правила вывода ИП. Оформление ИП как ФАТ 23

19. Теорема об общезначимости формул ИП, получающихся из общезначимых по любому из 4-х правил вывода ИП 24

20. Полнота и непротиворечивость ИП. Теорема Гёделя. Тезис Чёрча 25

21. Алгоритмы. Определение (интуитивное) алгоритма. Свойства алгоритмов. Направления поисков точного определения алгоритма. Вычислимые функции. Проблема алгоритмической неразрешимости 25

22. Рекурсивные функции. 3 простейших ПРФ (примитивно-рекурсивных функций). Оператор суперпозиции. Примеры 27

23. Оператор ПР (примитивной рекурсии). Доказать, что функции , , , , — ПРФ 28

24. Оператор минимизации. Частично-рекурсивные функции. Доказать, что — ЧРФ. Точное определение алгоритма. Тезис Чёрча 30

25. Машина Тьюринга. Тьюринговая функциональная схема. Точное определение алгоритма. Тезис Тьюринга 32

26. Функции, вычислимые по Тьюрингу. Доказать, что 3 простейших ПРФ — вычислимы по Тьюрингу 35

27. Геделева нумерация МТ. Примеры: по номеру найти МТ и по МТ записать номер 37

28. Самоприменимость МТ. Теорема об алгоритмической неразрешимости проблемы самоприменимости 37

29. Нормальные алгоритмы Маркова. Точное определение алгоритма. Примеры 39

Литература 42

1. Определение формальной аксиоматической теории (фат). Секвенции (выводы). Формулы. Построение формул. 5 свойств выводов

Различают неформальную и формальную аксиоматические теории:

• Неформальная (интуитивная) аксиоматическая теория — теория, в которой правила логики явно не заданы (геометрия, арифметика, теория вероятностей и т. п.).

• Формальная аксиоматическая теория — теория, в которой правила логики явно заданы.

Формальная аксиоматическая теория (ФАТ) – теория, в которой определены:

• Выражения (конечные последовательности символов).

• Формулы (подмножество выражений — последовательность символов определенного вида; стержень теории; обычно количество формул в данной теории составляет счётное множество).

  • Алфавит (счётное число символов, часто — латинские буквы).

  • Связки между формулами и правила их записи. Число связок всегда конечно. Связки бывают 1-го порядка (связывающие одну формулу; например, в тригонометрии), 2-го порядка (связывающие две формулы; например, в арифметике). Теоретически связки могут быть и -го порядка, связывающие между собой формул.

  • Скобки двух видов — правая и левая — нужны для того, чтобы определять порядок действий в формулах.

• Аксиомы данной теории (конечное число формул объявляются аксиомами).

• Правила вывода в рамках данной теории (правила вывода, позволяющие из одних формул получать другие — это действия с формулами; обычно количество правил вывода — конечное множество).

Построение формул:

1. Объявляются первичные (атомарные) формулы. Часто первичные формулы обозначаются заглавными буквами латинского алфавита.

2. Если — некоторая (уже построенная) формула и — связка 1-го порядка, то — тоже формула. Если и — две построенные формулы и — связка 2-го порядка, то — тоже формула, и, в общем случае, если — построенных формул и — связка порядка , то — тоже формула.

3. Любая формула данной теории либо сама является первичной, либо построена из первичных формул с помощью конечного числа применения правила №2.

Пусть («гамма») — произвольное конечное множество формул (возможно, пустое), используемых в качестве посылок вывода (гипотез).

Выводы (секвенции). Заметим, что слово секвенция означает «последовательность».

Далее следует считать, что вывод — это последовательный список формул, каждая из которых выводится из аксиом или предыдущих формул при помощи правил вывода.

Формула называется непосредственным следствием формул , если может быть получена из этих формул с помощью однократного применения какого-либо правила вывода .

Вывод (секвенция) — последовательность формул , каждая из которых либо является аксиомой, либо выводится из одной или нескольких предыдущих формул этой последовательности по одному из правил вывода.

Теорема — последняя формула вывода. Иначе говоря, теорема аксиоматической теории — формула, которая может быть выведена при помощи правил вывода.

Формула называется следствием множества формул тогда и только тогда, когда существует такая последовательность формул , каждая из которых либо аксиома, либо формула из , либо непосредственное следствие предыдущих формул. Эта последовательность формул называется выводом из ( — « есть следствие формул » или « можно вывести из формул »). Если 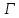— пустое множество формул, то есть следствие аксиом: — то есть теорема. Если из некоторых формул следует любая формула данной теории, то это значит, что формулы противоречивы: . Если состоит из формул , то вывод из можно записать так: . Формулы из множества называются посылками или предположениями.

Свойства выводов:

1. !

2. Если , то («порядок формул не имеет значения»).

3. Если и — любая формула, то («лишняя формула не мешает»).

4. Если и , то («удаление выводимой формулы»).

Пусть — вывод формулы из . То есть .

Тогда если среди встречается формула , то каждое её вхождение заменяем последовательностью формул, составляющих вывод из .

Таким образом, получаем вывод из .

5. Если из формул выводится , а из набора формул выводится формула , то из набора формул выводится формула .

Запишем вывод формулы из . Каждое вхождение в этот вывод заменим выводом из . Получим вывод из .