Условие Якоби
Пусть для вариационной задачи с закрепленными границами найдено решение уравнения Эйлера и определены функции и . Рассмотрим дифференциальное уравнение, которое носит название уравнения Якоби:
.
(18)
Определение.
Будем
говорить, что для уравнения (18)
выполнено
условие Якоби, если уравнение (18)
с граничными условиями
,
при любом
имеет
только тривиальные решения.
Добавление
условия Якоби к уравнению Эйлера и
знакоопределенности функции
образует тот набор требований, который
обеспечивает существование экстремума
у интегрального функционала на множестве
допустимых функций. Отметим, что проверка
условия Якоби оказывается намного
проще, чем доказательство неравенства
из теоремы 2.
Предпошлем доказательству основной теоремы несколько вспомогательных утверждений.
Лемма
2. Пусть
при всех
и выполнено условие Якоби. Тогда
уравнение Якоби имеет положительное
на всем отрезке
частное решение.
Доказательство.
Пусть
,
–
фундаментальная система решений
уравнения (18), то есть решения уравнения,
удовлетворяющие начальным условиям:
.
Легко видеть, что
на полуинтервале
:
в самом деле, в некоторой окрестности
точки
функция
положительна (она возрастает от нуля)
и не может обращаться в нуль ни в какой
другой точке
,
так как это противоречит условию Якоби.
Рассмотрим функцию
– решение уравнения (18), удовлетворяющее
начальным условиям
.
Зафиксируем
,
такое, что на множестве
функция
.
Такое
найдется, поскольку функция
непрерывна и положительна в точке
.
Рассмотрим теперь поведение функции
на
.
На этом отрезке
,
.
Выберем
таким, чтобы
.
Тогда
,
что и требовалось.
Следующее утверждение о непрерывной зависимости решения дифференциального уравнения от параметра удобнее формулировать и доказывать в векторной форме. Так как любое уравнение высшего порядка (в частности, уравнение Якоби) может быть переписано в виде системы дифференциальных уравнений, то факт непрерывной зависимости решения от параметра справедлив и для уравнений высших порядков.
Рассмотрим
систему линейных однородных
дифференциальных уравнений, коэффициенты
которой (матрицы-функции) зависят от
малого параметра
(19)
и
систему, соответствующую случаю
(20).
Лемма
3. Пусть
матрицы
имеют непрерывные на
коэффициенты, причем
.
Тогда, если
–
решение системы
(19) с заданными
начальными условиями, то
,
где
–
решение системы (20)
с теми же начальными условиями.
Доказательство.
Заметим, что из условий леммы следует
ограниченность семейства матриц
общей
постоянной:
.
Отсюда следует, что и семейство решений
с фиксированными начальными условиями
также ограничены общей постоянной:
.
Перепишем задачу Коши для системы (19) в эквивалентном интегральном виде:
,
где
–матрица
Коши системы (20). Заметим, что
,
а
.
Следовательно,
.
Лемма доказана.
Лемма
4. Пусть
при всех
и уравнение
(21)
имеет
положительное на отрезке
частное решение. Тогда
при любых непрерывно дифференцируемых
функциях
,
удовлетворяющих условиям
.
Доказательство. Обозначим
частное решение уравнения (21), положительное
на
.
Тогда функция
определена на
,
дифференцируема на этом отрезке и
удовлетворяет уравнению
.
Далее, для любой функции
,
удовлетворяющей условиям леммы,
,
следовательно,
,
что и требовалось доказать.
Теорема 3. Пусть функция
обладает
следующими свойствами:
является решением уравнения Эйлера с заданными краевыми условиями;
функция
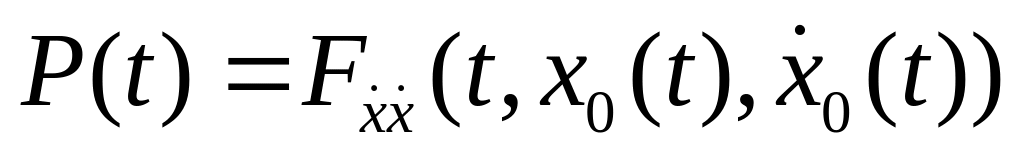строго положительна (строго отрицательна)
на отрезке
;для уравнения (18) выполнено условие Якоби.
Тогда функция является точкой локального минимума (максимума) функционала (16) на множестве функций с закрепленными границами.
Доказательство. Из леммы 2 следует, что уравнение Якоби имеет положительное на отрезке частное решение. Из леммы 3 следует, что найдется такое , при котором уравнение
также имеет положительное на
частное решение. Из леммы 4 следует,
что тогда
или
.
Далее, с учетом условия
,
имеем
;
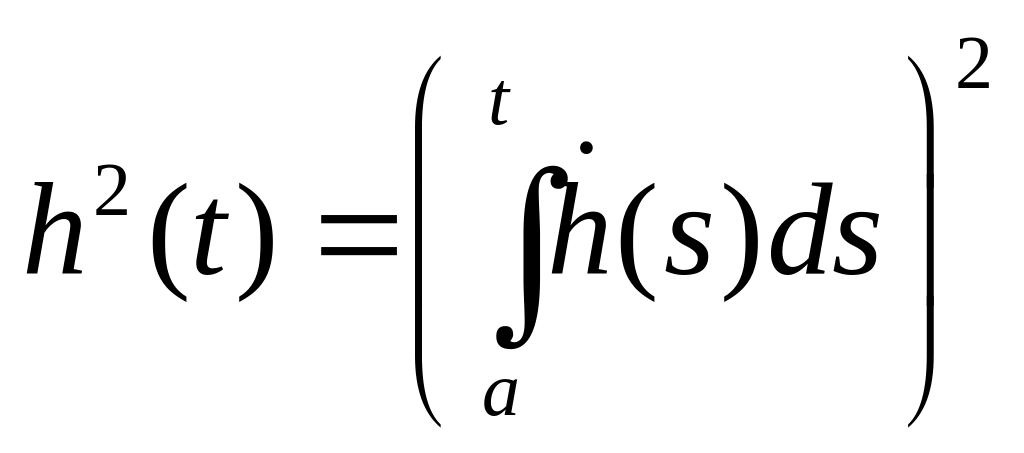применяя неравенство Коши–Буняковского,
получаем:
.
Объединяя это неравенство с предыдущим,
имеем окончательно:
.
Для завершения доказательства остается сослаться на теорему 2.
Отметим, что в теореме 3 первое и второе условия являются также и необходимыми. Выполнение условия Якоби не является необходимым для существования у функционала экстремума, однако, как показывает следующий пример, без него теорема перестает быть верной.
Пример 3. Рассмотрим задачу минимизации функционала
,
на классе функций, удовлетворяющих
условиям:
.
Решаем уравнение Эйлера, получаем
семейство экстремалей
,
из которых граничным условиям
удовлетворяют все функции вида
.
Второе условие теоремы 3 также выполнено:
.
Непосредственной подстановкой
убеждаемся, что
.
Теперь рассмотрим семейство функций
.
Нетрудно убедиться в том, что
,
то есть ни одна из функций, являющихся
решением уравнения Эйлера не доставляет
минимума рассматриваемому функционалу.
Причина, очевидно, в том, что в данном
примере не выполнено условие Якоби.
Действительно, уравнение Якоби
с краевыми условиями
имеет решение
,
не являющееся тождественно нулевым.