Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Пермский государственный технический университет»

Кафедра вычислительной математики и механики

Основы вариационного исчисления - III

Методические указания

и варианты заданий

для самостоятельной работы студентов

III курса специальностей км и дпм

Издательство

Пермского государственного технического университета

2011

Составитель: в.В. Малыгина

УДК 517 (075.8)

О75

Рецензент:

канд. физ.-мат. наук, доцент кафедры ВММ К.М. Чудинов

Основы вариационного исчисления. Ч. III: метод. указания и варианты заданий для самостоятельной работы студентов III курса специальностей КМ и ДПМ / сост. В.В. Малыгина. – Пермь: Изд-во Перм. гос. техн. ун-та, 2011. – 23 с.

Данное методическое пособие является продолжением пособий «Основы вариационного исчисления – I» и «Основы вариационного исчисления – II», сохраняя их обозначения и терминологию, а также продолжая нумерацию формул, примеров и заданий. Часть III посвящена достаточным условиям экстремума интегральных функционалов.

УДК 517 (075.8)

© ГОУ ВПО

«Пермский государственный

технический университет», 2011

Достаточные условия экстремума

В первой и второй части нашего методического пособия было показано, что решение уравнения Эйлера (или его обобщений) позволяет определить класс экстремалей, то есть кривых, на которых возможен экстремум. Точнее сказать, теорема о необходимом условии экстремума утверждает, что ни на каких иных кривых, кроме тех, которые являются решением уравнения Эйлера, экстремум достигаться не может. Но всегда ли экстремум достижим на экстремалях? И если да, то каков характер экстремума – максимум или минимум? Ни одно из приведенных выше утверждений не дает ответа на этот вопрос.

Конечно, возможна простая и приятная ситуация, когда вариационная задача имеет ясно выраженный геометрический и физический смысл, из которого сразу следует, что функционал обязательно имеет экстремум, и к тому же понятно – максимум это будет или минимум. Тогда, если экстремаль определяется однозначно, то никаких дополнительных исследований не понадобится: эта экстремаль и есть решение вариационной задачи.

Если же дополнительной информации о свойствах функционала нет, то необходимы формальные условия, гарантирующие наличие у данного функционала экстремума и разделяющие максимум с минимумом.

Установлению таких – достаточных – условий максимума и минимума функционалов интегрального вида посвящена третья часть нашего методического пособия.

1. Вторая вариация

Снова обратимся к функции одной переменной и вспомним, как решалась для нее аналогичная задача. Наряду с необходимым условием экстремума (обращение в нуль первой производной) в курсе математического анализа доказывался ряд достаточных условий экстремума. Проще всего обобщается на случай функционалов следующий признак: если вторая производная сохраняет знак в точке экстремума, то в этой точке минимум – если вторая производная положительна, и, соответственно, максимум – если вторая производная отрицательна.

Чтобы обобщить эту теорему, нам нужно ввести аналог второй производной. Так как аналогом первой производной (точнее, дифференциала) оказалась вариация функционала, то естественно продолжить аналогию и ввести понятие второй вариации функционала по той же схеме.

Определение. Второй вариацией функционала в точке назовем число

.

Как и раньше, в центре нашего внимания будет интегральный функционал

(16)

для которого решается задача отыскания максимума или минимума на множестве функций, проходящих через две фиксированные точки: .

Напомним, что для этой вариационной задачи первая вариация функционала (16) имеет вид:

.

Найдем для этой же задачи вторую вариацию функционала (16). По формуле второй вариации, применяя интегрирование по частям и условие закрепления концов, получаем

.

В дальнейшем для краткости будем полагать:

, .

Тогда вторая вариация примет вид

.

Следующая теорема показывает, что знак второй вариации действительно тесно связан с характером экстремума функционала.

Теорема 1. Пусть функционал , – точка экстремума функционала, причем в этой точке существует вторая вариация. Тогда:

• если – точка минимума, то при всех ;

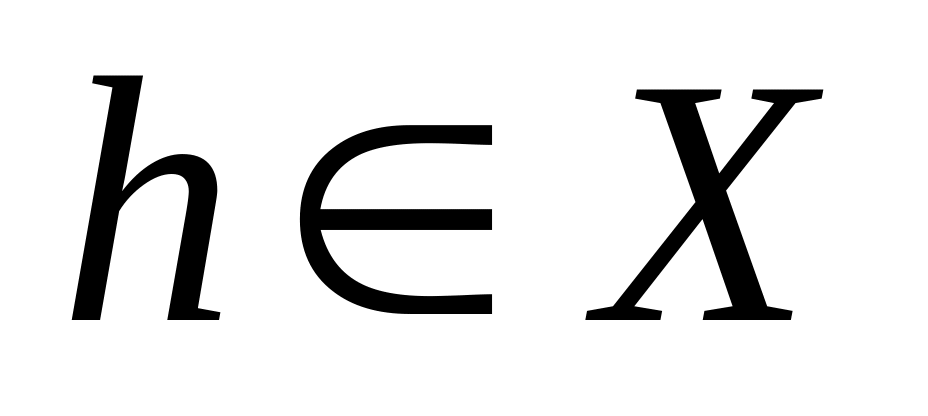
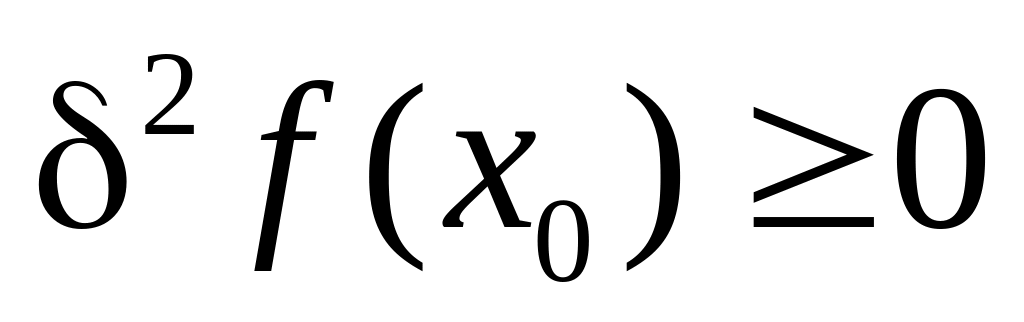• если – точка максимума, то при всех .

Доказательство этих утверждений проводится по одной схеме, так что ограничимся только первым. Пусть – точка минимума нашего функционала. Предположим, что при некотором и рассмотрим функцию одной вещественной переменной . Так как при всех достаточно малых справедливо неравенство

,

то есть точка локального минимума функции . Легко видеть, что , . Согласно необходимому условию экстремума, . По предположению, , но тогда и в точке у функции – максимум. Противоречие.

Следствие. Пусть – точка минимума (максимума) функционала (16). Тогда (соответственно, ) .

Доказательство. Пусть, ради определенности, – точка минимума. Предположим, что в некоторой точке выполнено неравенство . Так как функции и непрерывны на , то существуют такие постоянные , что , а на некотором ненулевом отрезке . Рассмотрим непрерывно дифференцируемую функцию , отличную от нуля при и равную нулю при . Положим и найдем знак второй вариации на этой функции. По определению второй вариации имеем:

,

что противоречит теореме 1.

После знакомства с теоремой 1 возникает естественная гипотеза: если потребовать, чтобы вторая вариация функционала на экстремали сохраняла знак, не получим ли мы тогда (аналогично ситуации для функций) искомое достаточное условие максимума и минимума соответственно?

К сожалению, это предположение не верно, как показывает следующий простой пример.

Пример 1. Найдем экстремали функционала ,

удовлетворяющие граничным условиям .

Легко видеть, что решением уравнения Эйлера являются функции и , из которых граничным условиям удовлетворяет только первая. Так как

, а ,

то при . Следовательно, вторая вариация положительна на экстремали.

Тем не менее, функция не является точкой локального минимума для данной вариационной задачи. Очевидно, что . Покажем, что в любой, сколь угодно малой окрестности нулевой функции найдутся функции (удовлетворяющие граничным условиям), на которых функционал строго отрицателен.

Зафиксируем и построим семейство функций .

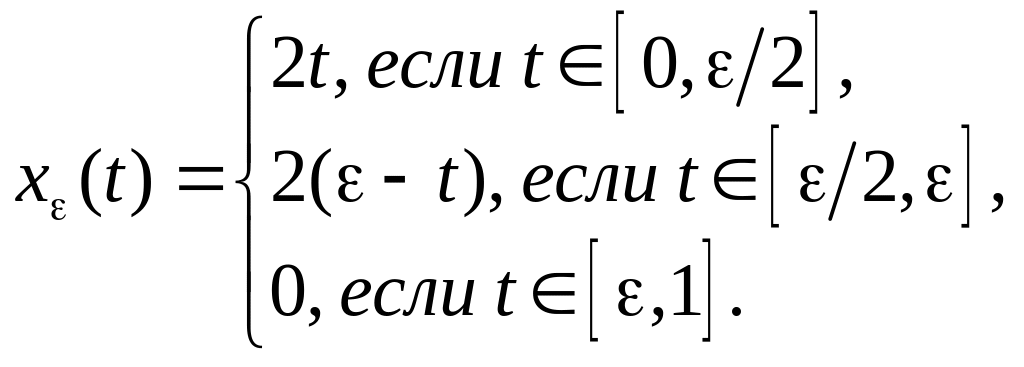
Все функции семейства непрерывны на отрезке и удовлетворяют граничным условиям. Вычислим :

.

Следовательно, в любой сколь угодно малой окрестности нуля функционал принимает отрицательные значения. Это и означает, что функция не является точкой локального минимума.