Изопериметрическая задача

Интересный класс задач на условный экстремум образуют так называемые изопериметрические задачи. Классической задачей такого вида (давшей название всему классу задач) является задача Дидоны: найти замкнутую кривую, ограничивающую наибольшую площадь при заданном периметре. При этом и минимизируемый функционал (площадь) и ограничение (периметр) задаются определенными интегралами.

Рассмотрим задачу в общей постановке. Пусть на кривых с фиксированными концами , функционал

достигает своего минимального (максимального) значения, причем интегралы

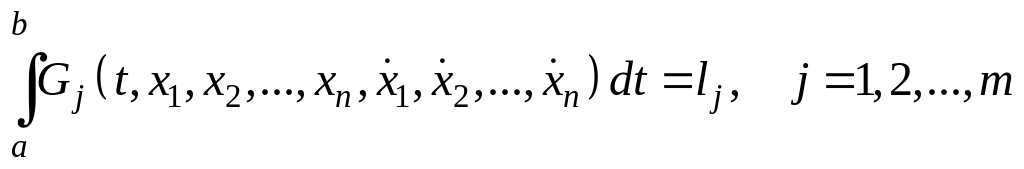
обладают заранее заданными значениями . Функции и считаются дважды непрерывно дифференцируемыми.

На первый взгляд кажется, что интегральные ограничения существенно усложняют задачу, и к изопериметрической задаче неприменимы методы предыдущего раздела. Однако оказалось, что изопериметрическую задачу остроумным приемом можно свести к задаче на условный экстремум с функциональными условиями связи.

Обозначим

.

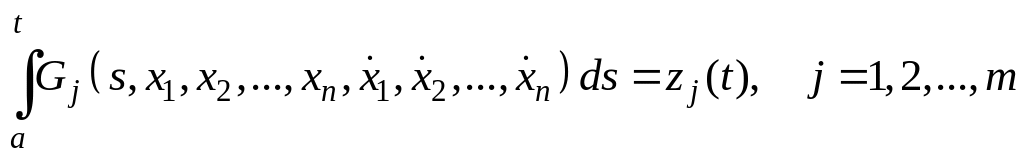Тогда

– новые условия связи, уже дифференциально-функционального вида, а изопериметрические условия превращаются в граничные условия:

.

Таким образом, задача свелась к задаче на условный экстремум, для которой выше был приведен алгоритм решения. Следуя ему, составляем вспомогательную функцию

,

для которой система уравнений Эйлера имеет вид:

.

Но так как , то , а тогда

.

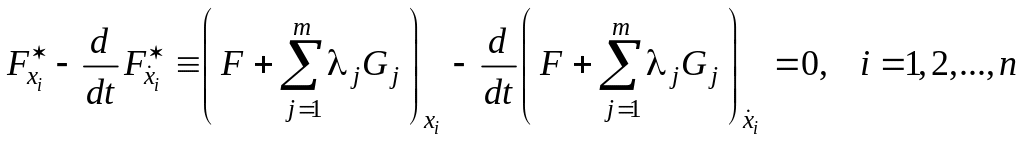Следовательно, для изопериметрической задачи в качестве функции Лагранжа можно взять функцию

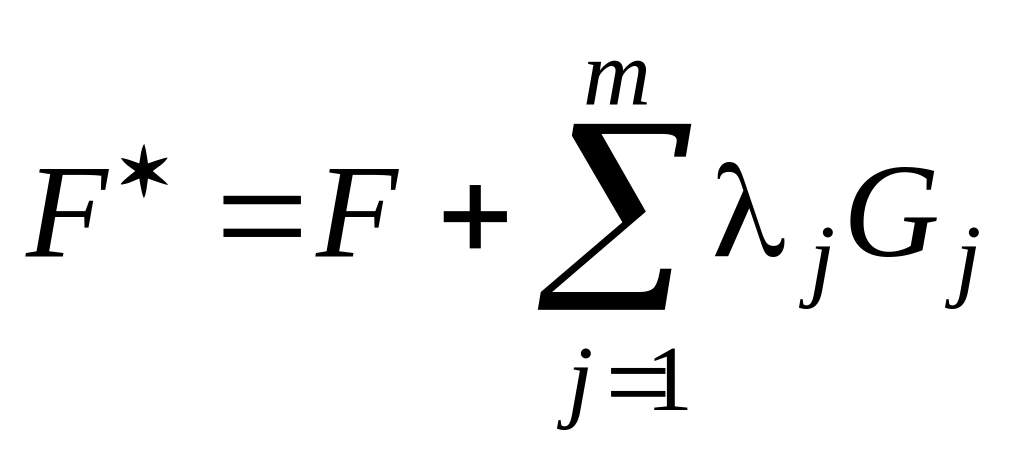
с постоянными множителями . Далее для функции , как и ранее, выписывается и решается система уравнений Эйлера, а для определения произвольных постоянных и параметров используются граничные и изопериметрические условия. То обстоятельство, что множители оказываются постоянными, безусловно, упрощает решение задачи.

Пример 9. Найти экстремум функционала

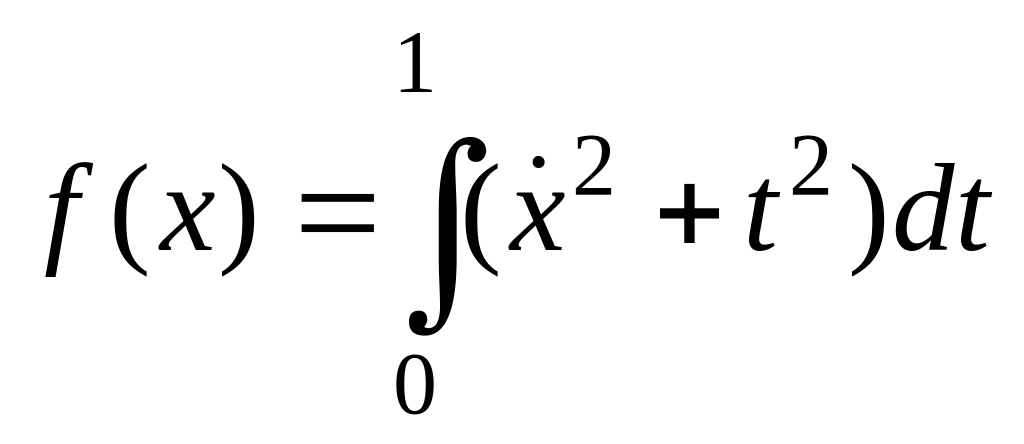
на классе функций, удовлетворяющих граничным условиям , и дополнительному условию .

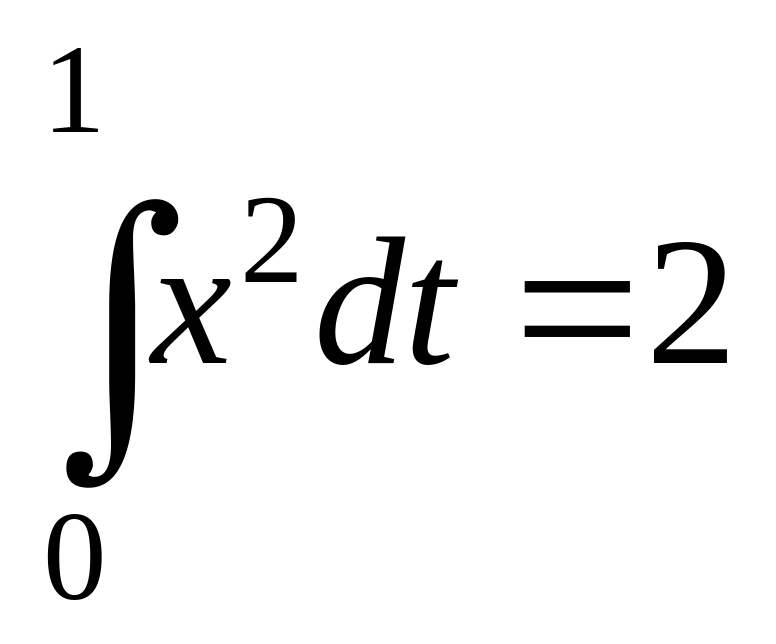Решение. Поставленная задача, очевидно, относится к классу изопериметрических задач, поэтому, согласно приведенной выше схеме, запишем вспомогательную функцию , для которой составим уравнение Эйлера: . Так как знак неизвестен, решение уравнения Эйлера следует провести для каждого из трех случаев: , и .

1. Пусть , тогда решение уравнения Эйлера имеет вид

.

Подставляя граничные условия, находим , то есть . Но это решение не удовлетворяет условию , следовательно, при решений у задачи нет.

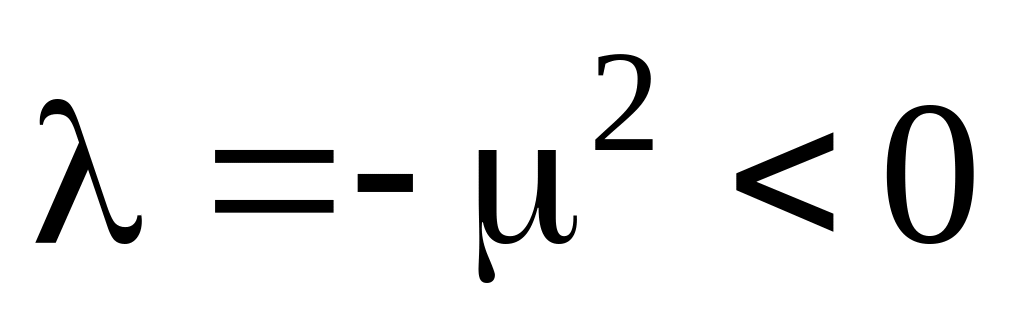2. Пусть , тогда решение уравнения Эйлера имеет вид

,

из граничных условий снова получаем , а , то есть при задача также не имеет решений.

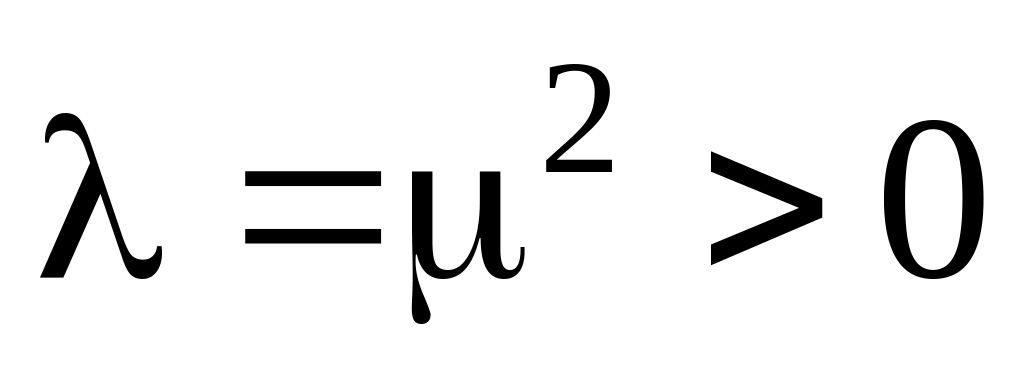3. Пусть , тогда решение уравнения Эйлера имеет вид

,

подставляя граничные условия, находим , – любое число, . Следовательно, , где . Определим через изопериметрическое условие:

.

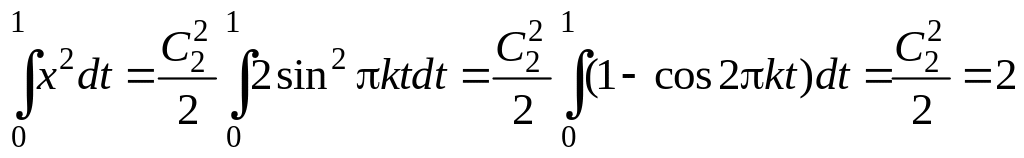Получаем , то есть . Так как , то можно оставить перед функцией один знак. Окончательно получаем, что данная вариационная задача имеет бесконечное множество решений вида:

.