Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Пермский государственный технический университет»

Кафедра вычислительной математики и механики

Основы вариационного исчисления - II

Методические указания

и варианты заданий

для самостоятельной работы студентов

III курса специальностей км и дпм

Издательство

Пермского государственного технического университета

2008

Составитель: в.В. Малыгина

УДК 517 (075.8)

О75

Рецензент:

канд. техн. наук, доцент кафедры ВММ И.Н. Бояршинова

Основы вариационного исчисления. Ч. II: метод. указания и варианты заданий для самостоятельной работы студентов III курса специальностей КМ и ДПМ / сост. В.В. Малыгина. – Пермь: Изд-во Перм. гос. техн. ун-та, 2008. – 58 с.

Данное методическое пособие является продолжением пособия «Основы вариационного исчисления – I», сохраняя его обозначения и терминологию, а также продолжая нумерацию формул, примеров и заданий. В часть II вошли разделы «Вариационные задачи на плоскости и в пространстве», «Вариационные задачи с подвижными границами» и «Задачи на условный экстремум».

УДК 517 (075.8)

© ГОУ ВПО

«Пермский государственный

технический университет», 2008

Вариационные задачи на плоскости и в пространстве

Функционалы, рассматриваемые в части I, имели областью определения множества функций одной переменной. Соответственно, уравнение Эйлера, к которому сводилась вариационная задача, представляло собой обыкновенное дифференциальное уравнение второго порядка.

Предположим, что вариационная задача должна быть поставлена и решена для функции нескольких (ради определенности – двух) независимых переменных: . Тогда, если мы продолжим изучение функционалов интегрального вида, то вместо функции следует рассматривать функцию , а вместо однократного интеграла появится двойной, взятый по некоторой области

. (4)

Уточним условия на функцию . Помимо непрерывности в области вместе со своими частными производными, она должна удовлетворять граничным условиям. Остановимся на этом подробнее. В части I для однозначного определения экстремали задавались значения и , т.е. значения функции на границах отрезка . Для функции двух переменных, продолжая аналогию, естественно задать условия на границе области . Обозначим эту границу и потребуем, чтобы

.

На функционал (4) легко обобщается необходимое условие экстремума.

Обозначим для удобства В этих обозначениях функция примет вид .

Теорема. Пусть функция – экстремаль функционала (4). Тогда является решением уравнения:

. (5)

Полученное уравнение представляет собой уравнение в частных производных второго порядка. Если функция зависит только от одной переменной, то оно превращается в уравнение Эйлера. В самом деле, если , то , , , и (5) принимает вид

.

Пример 5. Найти экстремаль функционала

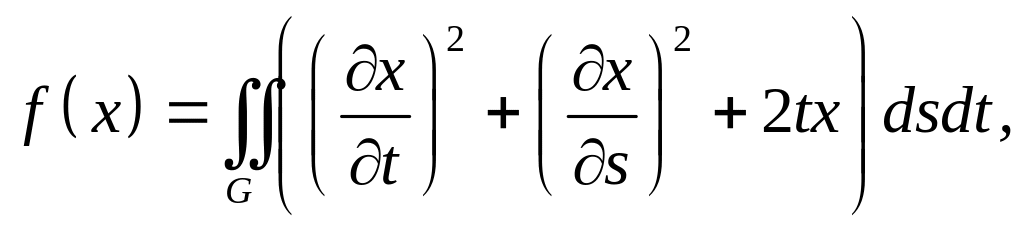
где – единичный круг с центром в начале координат, с граничными условиями .

Решение. Пользуясь введенными ранее обозначениями, запишем: . Уравнение (5) имеет вид: , то есть представляет собой уравнение эллиптического типа. Область, на которой ищется решение – внутренность круга (ограниченное множество), граница его – окружность, вдоль которой функция обращается в нуль. Следовательно, искомая экстремаль является решением задачи Дирихле для внутренности круга. Для круговых областей естественно переформулировать задачу, перейдя к полярным координатам :

(6)

Заменой переменных сводим уравнение (6) к однородному (с ненулевыми граничными условиями):

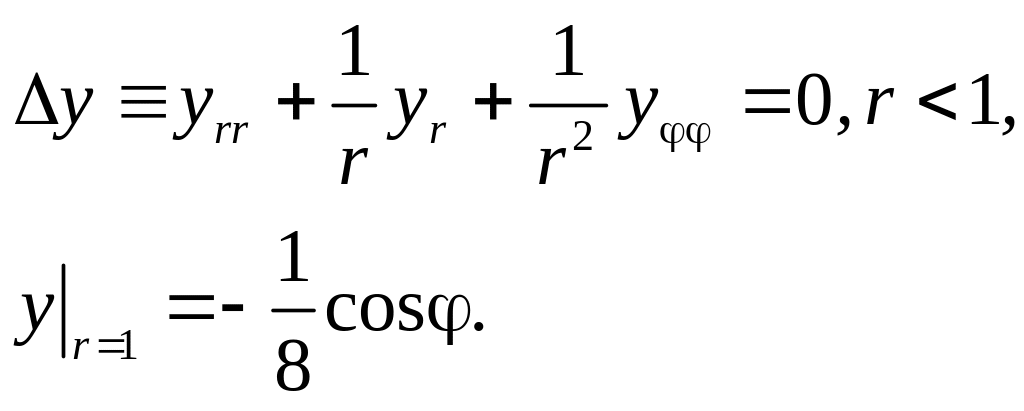(7)

Как известно из курса уравнений математической физики, решение задачи (7) имеет представление в виде ряда:

.

Учитывая граничные условия, получаем:

,

откуда по формуле для коэффициентов ряда Фурье имеем:

. Следовательно,

, а .

Если функция зависит от переменных, то вариационная задача ставится для функционала, который представляет собой кратный интеграл

(8)

по области . Обобщая вышеприведенную теорему, приходим к выводу, что функция, являющаяся экстремалью функционала (8), необходимо удовлетворяет уравнению:

, где

В частности, для случая трехмерной области получаем следующее необходимое условие экстремума.

Теорема. Пусть функция – экстремаль функционала

.

Тогда является решением уравнения:

, где . (9)

Пример 6. Пусть – прямой круговой цилиндр. Найти экстремаль функционала

,

удовлетворяющую граничным условиям: , .

Решение. Для данного функционала уравнение (9) принимает вид . Поскольку область – цилиндр, то задачу удобнее переформулировать в цилиндрических координатах . Из вида граничных условий заключаем, что задача является осесимметричной. Ее решение не зависит от и является функцией двух переменных: . Следовательно, экстремаль данного функционала есть решение следующей задачи:

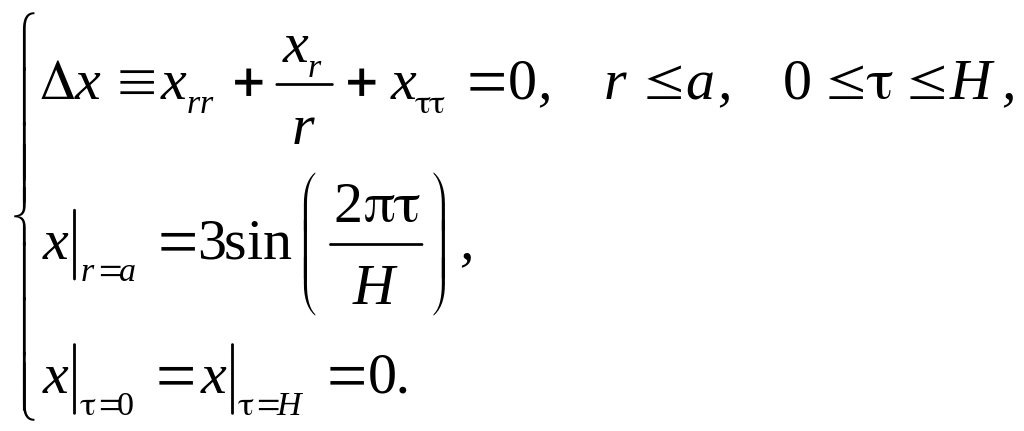
Полученное уравнение является уравнением в частных производных эллиптического типа и в совокупности с условиями на границе образует задачу Дирихле. Ее решение может быть получено методом разделения переменных.

Будем искать решение уравнения, удовлетворяющее граничным условиям в виде . Разделяя переменные, имеем:

.

Учитывая граничные условия, получаем, что функция является собственной функцией задачи Штурма–Лиувилля:

Как известно, собственные числа этой задачи , а соответствующие собственные функции . Для функции получаем уравнение

,

решением которого являются функции Бесселя мнимого аргумента: . Так как рассматриваемое уравнение и граничные условия являются линейными, то ряд, составленный из найденных функций и

,

при любых коэффициентах также является решением уравнения, удовлетворяющим однородным краевым условиям. Для определения используем последнее граничное условие:

.

Применяя теорему Стеклова, получаем: , при , то есть искомая экстремаль имеет вид:

.
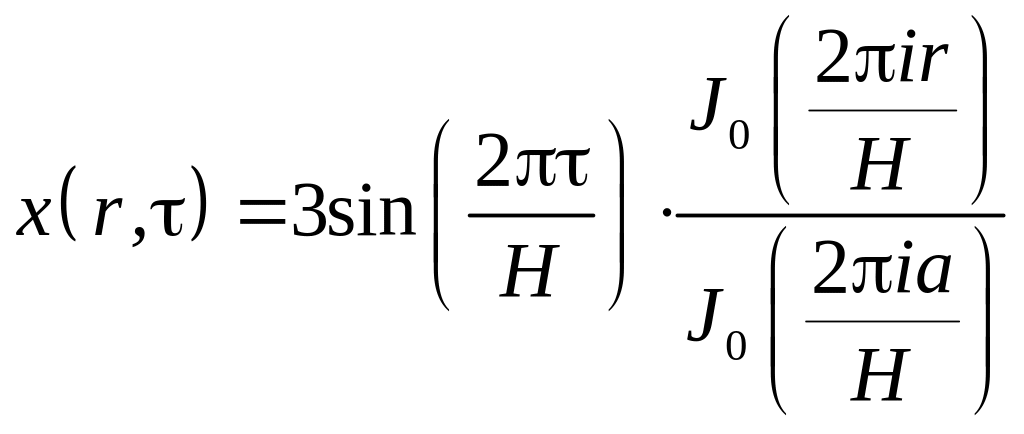