4. Расчет шпоночного соединения под колесом на тихоходном валу редуктора

Чаще всего применяются призматические (т. П6 [1, с. 149]) и сегментные (т. П7 [1, с. 150]). Соединения с помощью призматических и сегментных шпонок относятся к ненапряженным соединениям. ГОСТ 23360-78 предусматривает для каждого диаметра вала определенные размеры поперечного сечения шпонки. Поэтому при проектных расчетах размеры поперечного сечения шпонки b и h берут из табл. П6 [1, с. 149] и определяют рабочую длину шпонки ℓ_p. Длину шпонки ℓ=ℓ_p + b со скругленными или

ℓ = ℓ_p с плоскими торцами выбирают из стандартного ряда (т. П6).

При передаче вращающего момента на противоположных боковых узких гранях шпонки возникают напряжения смятия, а в продольном сечении – напряжение среза. У стандартных шпонок размеры b и h подобраны так, что нагрузку соединения ограничивают не напряжения среза, а напряжения смятия.

Рисунок 5 – Схема напряжений в шпоночном соединении

Рабочую длину шпонки определяем из условия прочности на смятии.

При d_k = 46 из т. П6 [1, с. 149] выбираем размеры для шпоночного соединения

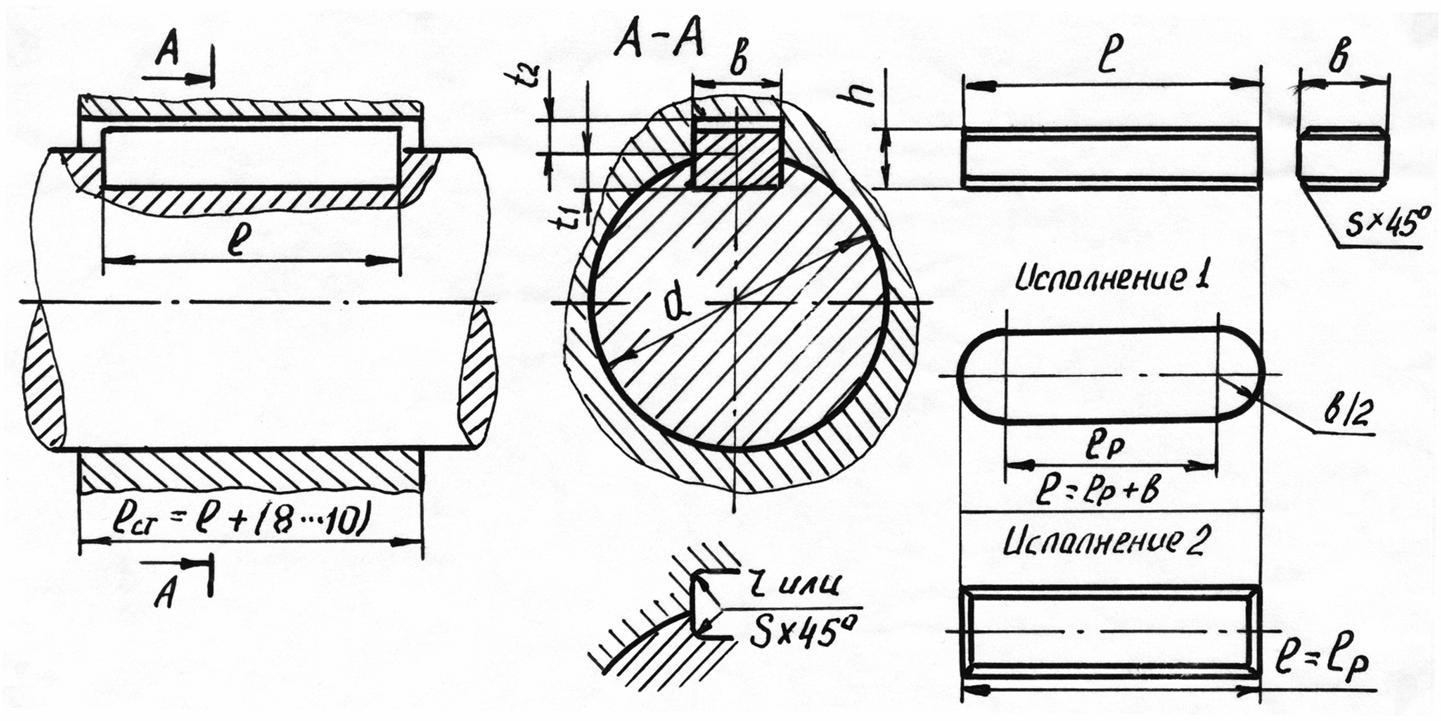
Рисунок 6 - Соединение призматической шпонкой

Определяем общую длину шпонки и округляем до ближайшего большого значения из стандартного ряда шпонок:

Принимаем из стандартного ряда: .

Следовательно, выбираем шпонку:

5. Расчет тихоходного вала

На вал от зубчатого колеса, подшипников и других деталей передаются окружные, радиальные и осевые силы, создающие в поперечных сечениях продольные и поперечные силы, изгибающие и вращающие моменты. Таким образом, вал испытывает сложную деформацию – изгиба (растяжения – сжатия) и кручения. Продольные силы создают в сечениях вала нормальные напряжения растяжения или сжатия небольшой величины, поэтому они в расчетах не учитываются.

Действующие на вал силы распределены по длине ступицы, ширине подшипника. При проектном расчете считаем эти силы сосредоточенными и приложенными на середине ширины зубчатого венца или подшипника. Эти сечения принимаем за расчетные. По длине вала место приложения нагрузки зависят от расположения зубчатого колеса и опор. Муфта создает силу, лежащую в плоскости, перпендикулярной к оси вала. После приведения этих сил к оси вала последний оказывается нагруженным поперечными силами и вращающим моментом. Косозубая цилиндрическая передача, кроме сил, лежащих в плоскостях, вызывает появление осевой силы, приложенной на зубьях. Приведение этой силы к оси вала дает осевую (сжимающую или растягивающую) силу и сосредоточенный изгибающий момент.

Исходные данные:

Силы, действующие на вал от косозубой цилиндрической передачи (определены при расчете передачи):

окружная - - действует в вертикальной плоскости;

радиальная - и осевая - (действует в горизонтальной плоскости);

Вращающий момент на валу - ;

Частота вращения вала - ;

Диаметр делительной окружности зубчатого колеса, установленного на валу - ;

Режим нагружения – постоянный;

Требуемый ресурс - ;

Диаметр вала под подшипники - ;;

Диаметр вала под колесо - ;

Расстояние между опорами вала, координаты точек приложения сил определяем по эскизной компоновке редуктора: a = 52,78 мм; b = 52,78 мм;

с = 59,5 мм.

Выходной вал редуктора соединен с приводным валом упругой муфтой.

Последовательность расчета:

1. Определяем радиальную силу от муфты, действующую на консольный участок вала по формуле [1, с.91, ф.4.2]

Принимаем действие этой силы в вертикальной плоскости (как и силы ), направленной на увеличение деформации вала от силы.

2. Используя эскизную компоновку редуктора, составляем расчетную схему вала (см. рисунок 7, а).

Опорные реакции в горизонтальной плоскости (см. рисунок 7, б):

,

Откуда,

,

,

.

Проверка правильности определения реакций:

4. Опорные реакции в вертикальной плоскости (см. рисунок 7, в):

,

Откуда,

,

,

.

Проверка правильности определения реакций:

.

5. Опорные реакции от силы(см. рисунок 7, г):

.

Откуда,

,

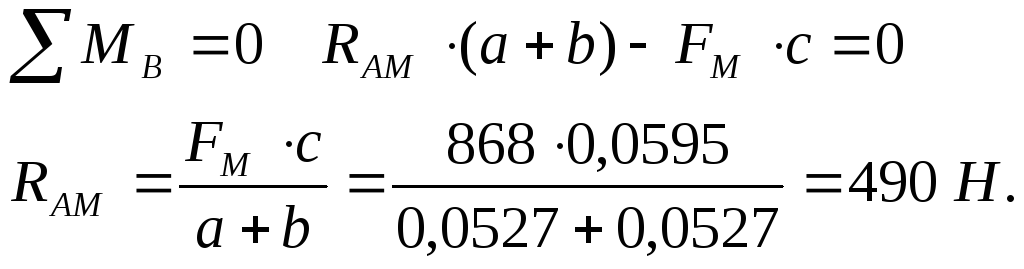
Проверка: .

Рисунок 7 - Расчетная схема вала

6. Суммарные реакции в опорах (приведенные в одну плоскость), которые будут использованы в качестве радиальных нагрузок при выборе подшипников качения:

7. Изгибающие моменты:

в горизонтальные плоскости (см. рисунок 7, б):

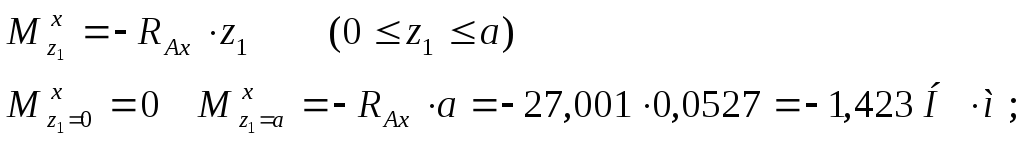
в вертикальной плоскости (см. рисунок 7, в):

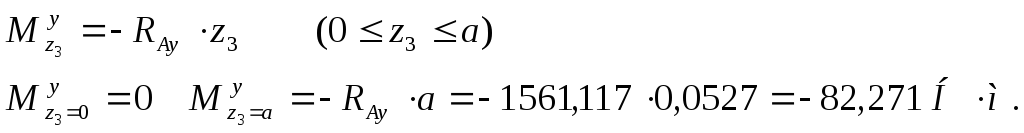
изгибающие моменты от силы (см. рисунок 7, г):

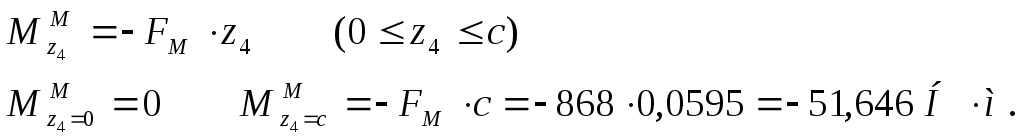
изгибающий момент в сечении С (под колесом):

8. Суммарный изгибающий момент в сечении под колесом (сечение С – это сечение наиболее нагруженное):

9. Принимаем: материал вала – сталь 45 [1, с.83, т.4.1];

;

механическая обработка вала – тонкая обточка; вал не подвергается поверхностному упрочнению.

10. Расчет на сопротивление усталости.

Для опасного сечения вала (сечение С) расчетный коэффициент запаса прочности определяется по формуле [1, с.93, ф.4.8], а коэффициенты S_σ и S_τ по формулам [1, с.93, ф.4.10] и [1, с.93, ф.4.11] соответственно:

; . т.к..

Коэффициент долговечности:

,

где циклов; т.к. ,то

Суммарные коэффициенты иопределяются по формулам

[1, с.95, ф.4.20]. В этих формулах значения эффективных коэффициентов концентрации напряжений и, зависят от вида концентраторов напряжений. В месте посадки колеса на вал имеется два типа концентраторов: ступенчатый переход с галтелью и шпоночная канавка. Для этих концентраторов по таблицам 4.3 и 4.4 [1, с.96-97] находим значенияи:

для ступенчатого перехода с галтелью (t = 3,5 мм, r = 2,0 мм приняты по рекомендациям [1, с.96]):

при ;и ;

для шпоночной канавки, выполненной пальцевой фрезой: ;.

Следовательно, большее влияние на прочность вала оказывает ступенчатый переход с галтелью r = 2,0 мм; поэтому для расчета принимаем ;. В этом сечении вал имеет сплошное круглое сечение.

По таблице 4.5 [1, с. 98] находим ; по таблице 4.6 [1, с.98] -; коэффициент, т.к. вал не подвергается поверхностному упрочнению.

Таким образом,

;

.

По формулам (4.14) определяем амплитудные значения напряжений:

МПа;

МПа,

Где моменты сопротивления W_и и W_р определены по формулам [1, с.94, ф.4.14]:

мм³;

мм³.

Тогда,

; .

Определяем коэффициент запаса прочности [1, с.93, ф.4.8]:

.

Следовательно, вал удовлетворяет условию прочности по сопротивлению усталости.