2.2.1. Допускаемые контактные напряжения

Допускаемые напряжения для зубьев шестерни и колесаопределяются по общей зависимости:

,

где - длительный предел контактной выносливости, определяемый по таблице 2.2 [1, с.31] в зависимости от материала зубчатого колеса и вида термической обработки по среднему значению твердости поверхностей зубьев, равной полусумме верхнего и нижнего значений их твердости.

Тогда, ;

- коэффициент, учитывающий шероховатость рабочих поверхностей зубьев, в данном случае принимаем при (притирка и обкатывание);

- коэффициент, учитывающий влияние скорости: повышение скорости вызывает увеличение толщины гидродинамического масляного слоя и уменьшение коэффициента трения. Принимаем ;

- коэффициент запаса контактной прочности, принимается из таблицы 2.2 [1, с.32].

Принимаем: ;

Определяем длительный предел контактной выносливости:

- коэффициент долговечности, учитывающий режим нагружений и требуемый ресурс передачи, принимается в пределах ,= 2,6 для материалов с однородной структурой (нормализованных, улучшенных) и 1,8 для поверхностно упрочненных материалов.

Определяем число циклов нагружений:

Определяем требуемый ресурс при постоянном режиме нагружений:

,

где - число вхождений в зацепление зуба рассчитываемого колеса за один оборот ();

- число оборотов в минуту, рассчитываемого колеса, мин^-1;

- требуемый ресурс передачи, ч. ().

;

.

Определяем коэффициент долговечности:

.

Не выполняется условие .

Принимаем: .

.

Тогда,

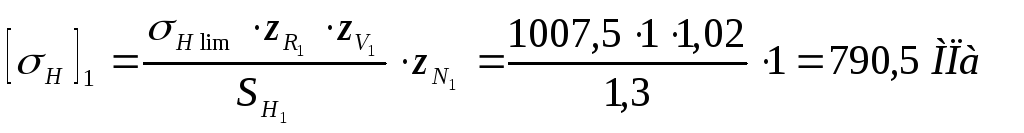
Для косозубых передач с твердостью шестерни ›350 HB расчетное допускаемое напряжение определяют по формуле [1. с.33]:

.

И это напряжение не должно превышать . В противном случае принимают.

Принимаем:

2.2.2. Допускаемые напряжения изгиба зубьев.

Допускаемые напряжения изгиба зубьев шестерни и колесаопределяют по формуле [1, с.34, ф.2.4]:

,

где - длительный предел выносливости при «отнулевом» цикле нагружений, выбирается по табл. 2.3 [1, с.34 ] в зависимости от материала и твердости зубьев;

- коэффициент запаса изгибной прочности выбирают по табл. 2.3 [1, с. 34];

- коэффициент долговечности, принимаемый в пределах ,

где - показатель степени кривой усталости;

- требуемый ресурс рассчитываемого зубчатого колеса в циклах.

;

.

Принимаем: ;;;; при.

.

Принимаем:

.

Принимаем: .

Тогда,

2.3. Проектный расчет на прочность закрытых зубчатых передач редукторов

Предварительно геометрические размеры передачи определяют расчетом на контактную выносливость зубьев.

Исходные данные (получены при кинематическом расчете):

- вращающий момент на шестерне;

- вращающий момент на колесе;

- частота вращения колеса;

- передаточное число;

- допускаемое контактное напряжение;

- допускаемое напряжение изгиба зубьев шестерни;

- допускаемые напряжения изгиба зубьев колеса.

Рисунок 3- Цилиндрическая зубчатая передача

Определяем предварительное значение межосевого расстояния: , мм [1, ф. 2.6, с.36]

,

где - вращающий момент колеса;

коэффициент К в зависимости от поверхностной твердости зубьев шестерни и колеса имеет значение 8;

.

.

Уточняем найденное значение межосевого расстояния [1, с.36, ф. 2.7]:

,

где для косозубых и шевронных зубчатых колес

- коэффициент нагрузки.

Коэффициент , учитывающий внутреннюю динамическую нагрузку, зависит от окружной скоростии степени точности изготовления передачи. Окружная скорость определяется по формуле [1, с.36, ф.2.9]:

.

Степень точности выбирают по таблице 2.4 [1,с.37]. Значения коэффициента выбираются по таблице 2.5 [1, с.37].

Принимаем: 8-ю степень точности, .

Коэффициент , учитывающий неравномерность распределения нагрузки по длине контактных линий, определяется по номограмме [1, рис 2.4, с.38] в зависимости от коэффициентов ширины, схемы передачи и твердости зубьев,

где - коэффициент ширины венца зубчатого колеса,

Принимаем: ;

;

.

Коэффициент , учитывающий неравномерность распределения нагрузки между одновременно зацепляющимися парами зубьев связи с погрешностями изготовления шестерни и колеса, определяется по следующей приближенной зависимости [1, с.39, ф.2.10]:

,

где - число, обозначающее степень точности передачи;

Принимаем:

.

Тогда,

.

Полученное значение межосевого расстояния округляем до ближайшего стандартного значения, получаем.

Определяем ширину венца колеса и округляем до ближайшего целого значения:

.

Принимаем: =50 мм

Определяем ширину венца шестерни и округляем до ближайшего целого значения:

;

.

Принимаем; =56 мм

Определение нормального модуля зубчатых колес производится при следующих условиях.

Значение модуля должно быть в пределах

Минимальный модуль определяют из условия прочности зубьев на изгиб по известному межосевому расстоянию по следующей зависимости [1, с.39, ф.2.11]:

,

где для косозубых и шевронных передач.

=1,781

.

Максимально допустимый модуль определяют из условия неподрезания зубьев у основания [1, с.40, ф.2.12]:

.

В диапазоне от ипринимают стандартное значение нормального модуляпо ГОСТ 9563-60.

Принимаем: =2 мм.

Определяем минимальный угол наклона зубьев [1, с.40, ф.2.14]:

;

.

Определяем суммарное число зубьев:

Полученное значение округляют в меньшую сторону до целого числа.

Принимаем: .

Определяем число зубьев шестерни [1, с.41, ф.2.16]:

;

.

Принимаем:

(передачу выполняют без коррекции ).

Принимаем:

Определяем число зубьев колеса [1, с.41]:

.

После вычисления чисел зубьев колес необходимо определить точное значение угла наклона зубьев с целью сохранения принятого межосевого расстояния :