
- •Задания и указания к решению контрольной работы по дисциплине «Теория вероятностей и математическая статистика».
- •Тема 1. Вероятность события. Алгебра событий (задачи 1-20). Перед выполнением задач необходимо изучить вопросы 1.2 - 1.3 первого раздела дисциплины и разобрать решение задач 1, 2, 3.
- •Решение типового примера.
- •Решение типового примера.
- •Тема 3. Дискретная случайная величина, ее числовые характеристики. (задачи 41-60). Перед выполнением задач необходимо изучить вопросы
- •1.4 Первого раздела дисциплины и разобрать решение задачи 7.
- •6) Построить график функции распределения f(х).
- •Решение типовой задачи.
- •Тема 4. Непрерывная случайная величина (задачи 61-80). Перед выполнением задач необходимо изучить вопросы 1.5 первого раздела дисциплины и разобрать решение задачи 8.
- •Решение типового примера.
- •Тема 5. Нормальный закон распределения (задачи 81-100). Перед выполнением задач необходимо изучить вопросы 1.5 первого раздела дисциплины и разобрать решение задачи 9.
- •Плотность нормального распределения;
- •Вероятность попадания этой случайной величины в интервал (25;40);
- •Вероятность заданного отклонения случайной величины от её математического ожидания.
- •Тема 6. Исследование вариационных рядов (задачи 101-120). Перед выполнением задач необходимо изучить вопросы 2.1, 2.2 второго раздела дисциплины и разобрать решение задачи 10.
- •Решение типового примера.
- •1) Получить вариационный ряд и построить гистограмму относительных частот;
- •2) Найти основные выборочные характеристики: , , , , ;
- •3) С надежностью 95% найти доверительный интервал для оценки генеральной средней .
- •Тема 7. Корреляционный анализ (задачи 121-140). Перед выполнением задач необходимо изучить вопросы 2.3 второго раздела дисциплины и разобрать решение задачи 11.
- •3) Нанести на чертеже исходные данные и построить прямую регрессии.
- •Решение типовой задачи
- •1) Найти коэффициент корреляции и сделать вывод о тесноте и направлении линейной корреляционной связи между признаками;
- •2) Составить уравнение прямой регрессии;
- •3) Нанести на чертеже исходные данные и построить полученную прямую регрессии.
Решение типового примера.
Задача
4. Посажено 5 деревьев, вероятность того,
что дерево приживется, равна
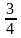 .
Какова вероятность, что приживется: а)
ровно 3 дерева, б) не менее трех деревьев.
.
Какова вероятность, что приживется: а)
ровно 3 дерева, б) не менее трех деревьев.
Решение:
Если n - число всех проведенных испытаний,
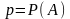 – вероятность появления события А
в каждом испытании,
– вероятность появления события А
в каждом испытании,

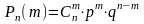
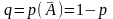 – вероятность не появления события А
в каждом испытании, тогда вероятность
– вероятность не появления события А
в каждом испытании, тогда вероятность
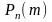 того, что событие А
появится m
раз в n
независимых
испытаниях вычисляется по формуле
Бернулли:
того, что событие А
появится m
раз в n
независимых
испытаниях вычисляется по формуле
Бернулли:
где
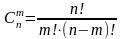 - число сочетаний из n
по
m.
- число сочетаний из n
по
m.
В нашей задаче дано: n=5; p= . Требуется найти: а) P5 (3 ); б) P5( m 3 ).
Задачу решаем, используя формулу Бернулли.
Найдем
q=1
- p=1-
=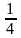 ,
,
а)
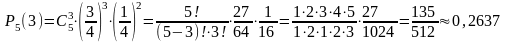
б) Искомое событие состоит в том, что из пяти посаженных деревьев приживутся или три, или четыре, или пять.
Таким
образом
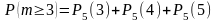
Вычислим отдельно каждое слагаемое:
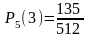 ;
;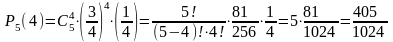 ;
;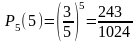 .
.
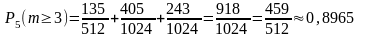
Задача 5. На станциях отправления поездов находится 1000 автоматов для продажи билетов. Вероятность выхода из строя одного автомата в течение часа равна 0,004. Какова вероятность того, что в течение часа выйдут из строя: а) два автомата, б) не менее двух автоматов.
Решение.
Формулу Бернулли удобно применять при n10. При большем значении n (n>10) применяют асимптотические формулы, т.е. приближенные формулы.
При больших значениях n (n) и малых p (p0), т.е. при a = np < 10, применяют формулу Пуассона:

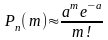
В нашей задаче дано: n=1000 (велико); p=0,004 (мало), тогда: np=10000,004=4<10.
а)
m=2;
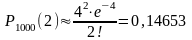 ,
значение вероятности нашли по таблице
1 (см. приложение).
,
значение вероятности нашли по таблице
1 (см. приложение).
б)
Пусть событие В
– выйдут из строя не менее двух автоматов,
т.е. от 2 до 1000. Рассмотрим событие
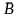 -
противоположное событию В,
которое состоит в том, что из строя
выйдет меньше двух автоматов, т.е. один
или ни одного, тогда:
-
противоположное событию В,
которое состоит в том, что из строя
выйдет меньше двух автоматов, т.е. один
или ни одного, тогда:
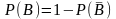 или
или
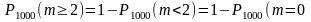 или
или
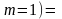
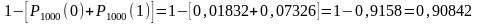
Задача 6. На предприятии работник за смену изготовляет 900 деталей. Вероятность того, что деталь окажется первого сорта, равна 0,9. Какова вероятность, что деталей первого сорта: а) будет ровно 800 штук;2) будет заключено между 800 и 860.
Решение.
а) Если число испытаний n велико, то применение формулы Бернулли приводит к громоздким вычислениям. В таких случаях применяют приближенную формулу, которая выражает локальную теорему Муавра – Лапласа.


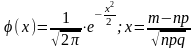
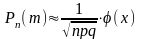 ,
где
,
где
Применяется
при больших значениях n
(n)
и 0<p<1
(не слишком малом), np
10. Функция
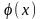 -
затабулирована (см. таблицу 2 приложения),
при этом следует учитывать, что;
-
затабулирована (см. таблицу 2 приложения),
при этом следует учитывать, что;
а)
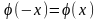 -
функция четная, таблица составлена для
x
0;
-
функция четная, таблица составлена для
x
0;
б) = 0 при x 4.
В
нашей задаче n=900
(велико, n>>10)
и p=0,9
(не очень малое число), m=800.
Найти:
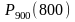 .
.
Найдем значение q= 1- p=1 - 0,9=0,1
Решение можно оформить следующим образом:
np = 9000,9 = 810
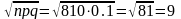
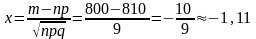
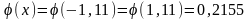 -
использовали свойство четности, значение
нашли
по таблице 2 приложения.
-
использовали свойство четности, значение
нашли
по таблице 2 приложения.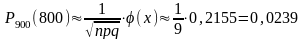 .
.
б) Для решения этой задачи используем интегральную теорему Лапласа.

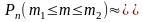 Ф(x2)
– Ф(x1),
где Ф(x)=
Ф(x2)
– Ф(x1),
где Ф(x)=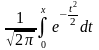
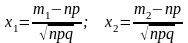
Применяется при вычислении вероятности того, что событие А в n независимых испытаниях появится не менее m1 и не более m2 раз при условии, что n велико (n), 0<p<1 (не слишком мало).
Функция Ф(x) называется интегральной функцией Лапласа, ее значения затабулированы (см. таблицу 3 приложения), при пользовании таблицей следует учесть, что:
а) Ф(-x)=- Ф(x) – функция нечетная;
б) Ф(x)=0,5 при x5.
В нашей задаче n=900 (велико), p=0,9 (не очень мало), также даны границы изменения m: m1=800; m2=860.
Найти:
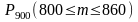 .
.
Найдем значение q= 1- p=1 - 0,9=0,1
Решение можно оформить следующим образом:
np=810;
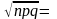 9
9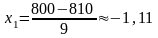 ;
;
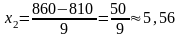
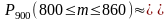 Ф(x2)-Ф(x1)=Ф(5,56)-Ф(-1,11)=Ф(5,56)+Ф(1,11)=
Ф(x2)-Ф(x1)=Ф(5,56)-Ф(-1,11)=Ф(5,56)+Ф(1,11)=
0,5 + 0,3665 = 0,8665
При нахождении значений Ф(x1) и Ф(x2) использовали свойство нечетности функции Ф(x) и Ф(5,56)=0,5 т.к. x>5, для нахождения Ф(1,11) пользовались таблицей 3 приложения.
