6. Волновое движение

Процесс распространения колебаний в пространстве

с течением времени – волновой процесс или волна.

Механичекие волны могут распространяться в упругой

среде. Простейшая модель упругой среды – материальные

точки, между которыми десйствуют упругие силы.

В плоской волне каждая мат.точка имеет координаты x,y. Пусть точка с координатой x=0 совершает кобание вдоль оси OY по закону: ,

Полагаем далее, что затухания нет, следовательно амплитуда колебаний для всех точек по оси OX

одинакова: 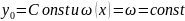. Смещение точек по оси OX не происходит (поперечная волна) Смещение первой точки нарушает равновесие второй точки и т.д.

Вдоль оси OX начнётся распространяться процесс колебаний c некоторой скоростью Заметим, что все частицы начинают движение от положения равновесия так же, как и первая, но с запаздыванием по времени на 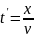. Тогда время начала колебаний произвольной точки вдоль оси OX будет функцией координаты. Можно сформулировать словесное описание такого процесса как: кая точка среды начинает своё колебательное движение как начинала его первая 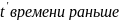. Соответственно математическая запись закона распространения колебаний 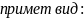y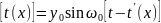

Итак, закон волнового движения, уравнение волны: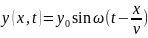

Важнейшим параметром волнового процесса является длина волны 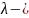это расстояние, на которое распространится волна за время, равное периоду колебания Т, то есть 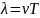. Поскольку период связан с линейной частотой ( числом колебаний за 1 секунду) ,то .

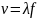Заметим, что когда через время t=T первая точка x=0 начнёт своё второе колебание, другая точка с координатой x= 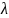начнёт своё, точно такое же движение, первый раз. Через некоторое время на оси

уже будет множество точек, которые имеют одинаковые значения 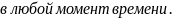Говорят, что они колеблются в одинаковой фазе. Не трудно понять, что любые две точки волны, отстоящие друг от друга на расстояние , будут обладать таким свойством. Тогда: кратчайшее расстояние между точками, колеблющимися в одинаковой фазе – длина волны.

Волновое число можно связать с длинной волны:

Кинематические уравнения по видам движения: координата, скорость, ускорение:

1. Уравнение поступательного движения: ;

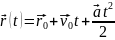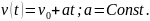
2. Уравнение вращательного движения: ; + ;

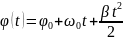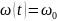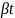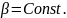
3. Уравнение колебательного движения: 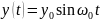; v(t) = .

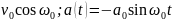Здесь = 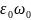; ; 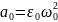- зависит от колебательных (упругих) свойств системы.

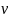4. Уравнение волнового движения: ; скорость волны зависит от упругих свойств среды.

Практические задачи.

Задача 1.

Скорость материальной точки задана уравнениями:

Найти кинематическое уравнение движения и траекторию.

1. Запишем условие в векторной форме:

2. Ускорение:

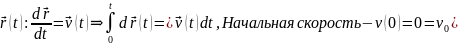3. по условию задачи.

4. Выберем начальное положение точки: .

Запишем кинематическое уравнение движения:

В координатной форме:

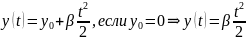
Для получения уравнения траектории необходимо исключить время :

Тогда уравнение траектории: 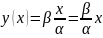- прямая линия.

Задача 2.

Материальная точка движется со скоростью Найти уравнение движения.

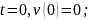
Начальные условия: -постоянный вектор

Решение.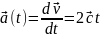 ; 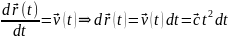Интегрируя , получим:

.

Движение твердого тела

Твердое тело – это совокупность материальных точек, расстояние между которыми в процессе движения остается неизменным.

Степень свободы твердого тела – число независимых переменных, описывающих состояние данной системы.

Для того чтобы “найти” твердое тело в Декартовой системе координат необходимо знать координаты трех его точек, не лежащих на одной прямой. Так как каждая точка имеет три координаты, то 9 координат достаточно, чтобы определить положение твёрдого тела в пространстве. Однако число координат (степеней свободы) можно сократить, используя свойство неизменности расстояний между выбранными точками. Т.о – число степеней свободы твёрдого тела в трёхмерном пространстве может сведено к 6 (шести).

Поступательным движением твердого тела назовем движение, при котором векторы перемещения материальных точек тела одинаковы за любой промежуток времени. Или любая прямая, проведенная в теле остается параллельна самой себе.

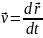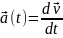; - одинаковы для всех точек тела.

При поступательном движении достаточно знать закон движения одной точки твердого тела.

Вращательное движение. При вращении вокруг неподвижной оси радиус-векторы точек твердого тела, относительно точек отсчета, взятых на оси за любые равные промежутки времени совершают повороты на равные углы.

Если взять в качестве координат угол поворота 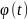, то любые точки будут иметь равные угловые скорости 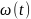и угловые ускорения .

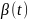Теорема Эйлера о произвольном движении твердого тела.

Произвольное движение твердого тела может быть представлено суммой двух движений: поступательного и вращательного относительно мгновенной оси.

Простые решения задачи о движении тв. тела возможны при поступательном движении и вращении, относительно неподвижной оси или ей параллельной.