Конспект лекций.

Часть I. Механика

Раздел 1. Введение

Математический аппарат физики. Векторы и операции с ними

Векто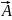р характеризуется модулем (длиной) и направлением. Любой вектор равен своей длине, умноженной на единичный вектор своего направления:

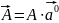
Вектор суммы векторов и 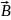, есть вектор 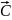, являющиеся диагональю паралелограмма, построенного на векторах и как на сторонах.

+ = . Длина вектора суммы:

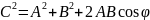
Вектор разности двух векторов и - есть вектор 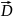, соединяющий концы вычитаемых векторов, приведенных к одному началу и направленный в сторону уменьшаемого.

=

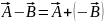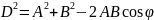
Изменение вектора (как по величине, так и по направлению): Если 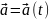, то

изменение за время 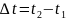, есть вектор 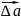(t)=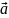 (t₂) - (t₁ ) Умножение векторов:

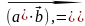
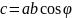
1. Скалярное произведение есть число: 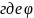- угол между векторами.

2. Векторное произведение есть вектор:

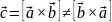
Длина вектора : .

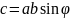Направление вектора : 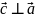, , 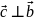если смотреть с конца

вектора , то направление кратчайшего поворота от первого вектора ко второму - против часовой стрелки.

Разложение вектора на составляющие:

операция, .

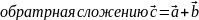Строим параллелограмм с диагональю и сторонами

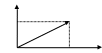
Проекция вектора на ось есть число, равное , где 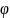- угол между осью и вктором.

Если взять оси декартовой системы координат, то:

- составляющие вектора.

–

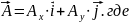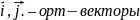
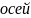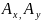, -проекции вектора на оси.

Момент вектора относительно точки и оси:

1. Момент вектора относительно точки О – это вектор 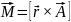Вектор 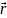-соединяет точку О с началом вектора

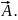
2. Момент вектора относительно оси, проходящей через точку O – это проекция вектора на эту ось.

Дифференцирование функций.

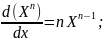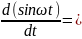
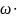1). 2). cos . Здесь dx- бесконечно малое изменение величины x, dt- соответственно, величины t.

Дифференцирование вектора: , длина и направление - функции времени. Тогда

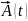вектор – коллинеарен (параллелен) исходному , характеризует изменение

вектора только по величине.

Вектор 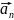– перпендикулярен исходному, характеризует изменение

вектора только по направлению.

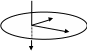
Пример. Пусть вектор меняется только по направлению, (вращается относительно своего начала), тогда производная от вектора будет равна: 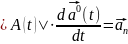. Найдём этот вектор.

Его направление совпадает с направлением вектора t), соединяющего концы двух векторов 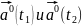Конец единичного вектора 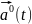описывает окружность единичного радиуса

и за бесконечно малое время dt опишет бесконечно малую часть этой окружности dS. При этом

длина дуги «почти» равна длине секущей (которая почти перпендикулярна к радиусу) т.е.

|d( 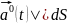=R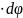 = | = 1 . Модуль вектора | .| = | .

Таким образом, вектор найден и по величине и по направлению.

Интегрирование.

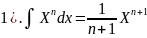+Const. 2). cos ;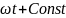

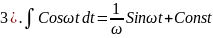
Если некоторая функция независимой переменной x есть 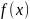, то 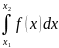численно равен площади под графиком

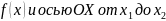
Раздел 2. Кинематика

Материальная точка. Система отсчета. Траектория. Перемещение и путь. Скорость и ускорение. Тангенциальное и нормальное ускорения. Классификация движения по ускорению. Кинематика прямолинейного и вращательного движений точки. Кинематика колебательного и волнового движений. Примеры, практические задачи.

Движение твердого тела. Степени свободы. Поступательное и вращательное движение твердого тела. Теорема Эйлера о произвольном движении твёрдого тела.

Механическое движение – это изменение положения (перемещение) тела в пространстве, относительно других тел.

Предварительно введем следующие упрощения:

1. От реальных тел мы перейдём к материальной точке (тело, размерами которого можно пренебречь в условиях нашей задачи)

2. Пусть тело отсчета есть точка O –, материальная точка M – тело, которое движется относительно O (тело отсчета неподвижно).

Вектор 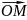, соединяющий точку отсчёта и движущуюся материальную точку – радиус-вектор 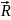. Если радиус-вектор меняется, то точка движется.

Системы отсчета:

1. Векторная система отсчета. Переменные величины: радиус- вектор, время.

1. Зависимость радиус-вектора точки от времени – уравнение движения:

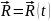
2. Скоростью движения материальной точки мы называем первую производную от

радиуса-вектора по времени:

3. Ускорением материальной точки мы называем первую производную от вектора скорости по времени (вторую производную от радиуса-вектора по времени):

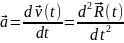
2. Декартова система отсчета. Тело отсчёта- начало прямоугольной системы координат О, три взаимно перпендикулярных оси ОX; OY; OZ . Положение точки определяется тремя числами-xyz - координатами. Если любая из координат меняется – точка движется.

Радиус-вектор в декартовой системе: Разложим радиус-вектор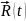 на составляющие по осям координаи: 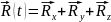Каждая сотавляющая равна своей длине, умноженной на единичный вектор оси: и т.д.

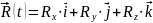. Здесь 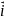, ,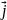 - орт-векторы (единичные) соответствующих осей. Проекции радиус-вектора на оси есть декартовы координаты точки.

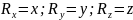
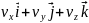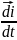= (учтено, что орты не меняются со временем т.е. =0 и тело отсчёта – начало системы координат)