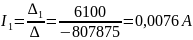МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

”МИНСКИЙ ГОСУДАРСТВЕННЫЙ ВЫСШИЙ

РАДИОТЕХНИЧЕСКИЙ КОЛЛЕДЖ”

Расчет электрических цепей постоянного и переменного токов

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

К курсовому проекту по предмету:

”Теоретические основы электротехники”

КП 31.591005.201ПЗ

Руководитель О.О. Щербакова-Шаблова

Учащийся В.Н. Грудько

2015

Расчёт линейных электрических цепей постоянного тока

Для электрической цепи, изображённой на рис. 1.1, выполнить следующее:

1. Составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;

2. Определить токи во всех ветвях схемы, используя метод контурных токов;

3. Определить токи во всех ветвях схемы на основании метода наложения;

4. Составить баланс мощностей для заданной схемы;

5. Результаты расчёта токов по пунктам 2 и 3 представить в виде таблицы и сравнить;

6. Построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.

R₃ R₅

I₃ I_k1 R₁ I_k3 I₅

E₁

I₄ E₁ I₆

R₄ I₁ r₀₁ R₆

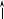
I_k2 I₂

E₂ r₀₂ R₂

Рисунок 1.1

Дано: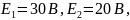

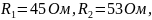
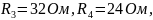
Определить:

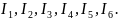
1) Составить систему уравнений, применяя законы Кирхгофа для определения токов во всех ветвях.

Произвольно задаём направление токов в ветвях

Составляем систему уравнений.

В заданной цепи пять ветвей, значит, в системе должно быть пять уравнений (m = 5). Сначала составляем уравнения для узлов по первому закону Кирхгофа. В нашей цепи три узла (2, 5, 4), значит, число независимых уравнений будет 3.

Составим три уравнения для любых 3-х узлов, например, для узлов А, Б и Г.

Узел 2:

Узел 5:

Узел 4:

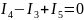
Всего в системе должно быть шесть уравнений. Три недостающих составляем для линейно независимых контуров. Задаёмся обходом каждого контура и составляем уравнения по второму закону Кирхгофа.

Контур 5425 ­­– обход против часовой стрелки

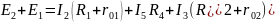
Контур 5125 ­­– обход по часовой стрелке

)

Контур 4234 ­­– обход по часовой стрелке

Мы получили систему из шести уравнений:

)

Подставляем в уравнение численные значения ЭДС и сопротивлений.

)

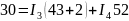
Решим систему с помощью определителей.

	1	-1	1	-1	0
	-1	1	0	0	-1
=	0	65	45	0	25	=	-807875
	45	65	0	0	0
	0	0	45	52	0
	0	-1	1	-1	0
	0	1	0	0	-1
=	50	65	45	0	25	=	6100
	20	65	0	0	0
	30	0	45	52	0
	1	0	1	-1	0
	-1	0	0	0	-1
=	0	50	45	0	25	=	-252800
	45	20	0	0	0
	0	30	45	52	0
	1	-1	0	-1	0
	-1	1	0	0	-1
=	0	65	50	0	25	=	-388650
	45	65	20	0	0
	0	0	30	52	0
	1	-1	1	0	0
	-1	1	0	0	-1
=	0	65	45	50	25	=	-129750
	45	65	0	20	0
	0	0	45	30	0
	1	-1	1	-1	0
	-1	1	0	0	0
=	0	65	45	0	50	=	-258900
	45	65	0	0	20
	0	0	45	52	30

Вычисляем токи: