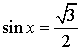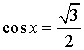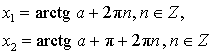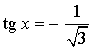Вопросы по математике и ответы к ним.

Алгебра.

1. Вопрос: Приближенное значение величины. Абсолютная и относительная погрешность величины.

Ответ: Приближенное значение величины - это число, которое лишь приближенно выражает истинное значение величины.

Абсолютная погрешность - это модуль разности между приближенным и точным значением величины ∆ = |A_T - A_H|, где A_Н - приближенное значение некоторого точного значения A_Т.

Относительная погрешность - это частное от деления абсолютной погрешности на модуль приближенного значения , или . Чтобы найти относительную погрешность в процентах, надо относительную погрешность умножить на 100 %.

2. Вопрос: Округление и погрешность округления (с недостатком, с избытком, с наименьшей погрешностью).

Ответ: Округление — математическая операция, позволяющая уменьшить количество знаков в числе за счёт замены числа его приближённым значением с определённой точностью.

1. Округление с недостатком – округление числа в меньшую сторону.

2. Округление с избытком – округление числа в большую сторону.

3. Округления с наименьшей погрешностью – округление числа в такую сторону, чтобы погрешность округления была минимальной.

3. Вопрос: Множества, подмножества, основные понятия и примеры.

Ответ: Множество – совокупность некоторых элементов. Пример: А = {2, 6, 15}.

Подмножество – это часть множества. Т. е. если каждый элемент множества В является также элементом множества А, множество В называется подмножеством множества А (обозначение - B ⊆ A или A ⊇ B).

4. Вопрос: Числовая функция, способы задания, примеры.

Ответ: Если даны числовое множество X и правило f, позволяющее поставить в соответствие каждому элементу x из множества X определённое число y, то говорят, что задана функция y = f(x) с областью определения X. Областью определения функции y = f(x) называют множество всех значений x, для которых функция имеет смысл.

Задать функцию - это значит указать правило, которое позволяет по произвольно выбранному значению x ∈ D(f) вычислить соответствующие значение y.

Способы задания:

1. Графический: функция задаётся графиком

2. Аналитический: функция задаётся формулой

3. Табличный: функция задаётся таблицей значений

Примеры: y(x)=x²

5. Вопрос: Четные, нечетные, периодические, монотонные функции.

Ответ: Если f(x)=f(-x), то функция четная, если f(x)=-f(-x), то нечетная.

Периодическая функция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (периода функции) на всей области определения.

Монотонная функция — это функция, которая всё время либо не убывает, либо не возрастает.

6. Вопрос: Предел функции в точке и на бесконечности. Свойства предела.

Ответ: Число b называется пределом функции f(x) в точке a, если для любой последовательности , которая сходится к a , соответствующая последовательность значений функции {f(x_n)} сходится к b.

Число b называется пределом функции f(x) на бесконечности или при x → ∞, если для любого существует число такое, что для всех из того, что |x|>M , выполняется неравенство |f(x)-b| < Є.

7. Вопрос: Арифметический корень n-ой степени. Степень с рациональным показателем (Определение и свойства).

Ответ:

К орнем n-й степени из числа а называется такое число b, n-я степень которого равна a, то есть

Степенью числа a > 0 с рациональным показателем r=m/n, где m - целое число, а n - натуральное ( n > 1), называется число , т.е.

8. Вопрос: Показательная функция, свойства и график.

Ответ:

9. Вопрос: Определение логарифма, свойства логарифмов.

Ответ:

10. Вопрос: Логарифмическая функция, свойства и график.

Ответ:

11. Вопрос: Функция y = cos x, свойства и график.

Ответ:

12. Вопрос: Функция y = sin x, свойства и график.

Ответ:

13. Вопрос: Функция y = tg x, y = ctg x, свойства и график.

Ответ: 13.1 y = tg x

Свойства функции y = tg x Обл. определения – x≠(π/2)+πn, nЄZ Множество значений функции: yЄR Периодическая T=π Нечётная функция Возрастает на всей области опр. Нули функции y(x)=0 при πn, nЄZ y(x)>0 при xЄ(0; π/2) и при сдвиге на πn, nЄZ y(x)<0 при xЄ(-π/2;0) и при сдвиге на πn, nЄZ

При x=(π/2)+πn, nЄZ функция не определена

Функция имеет точки разрыва

13.2 y = ctg x

Свойства функции y = ctg x Обл. определения – x≠0+πn, nЄZ Множество значений функции: yЄR Периодическая T=π Нечётная функция Убывает на всей области опр. Нули функции y(x)=0 при πn, nЄZ y(x)>0 при xЄ(0; π/2) и при сдвиге на πn, nЄZ y(x)<0 при xЄ(-π/2;0) и при сдвиге на πn, nЄZ

При x=0+πn, nЄZ функция не определена

Функция имеет точки разрыва

14. Вопрос: Радианная и градусная меры углов. Поворот точки вокруг начала координат. Ответ: Если угол содержит α° и одновременно измеряется x радиан, то  , где K° - постоянный коэффициент. Подставляя, например,   и  , получаем  . Наоборот,  , где  .

 

Поворот точки вокруг начала координат

Рассмотрим на координатной плоскости окружность радиуса 1 с центром в начале координат. Ее называют единичной окружностью. Введем понятие поворота точки единичной окружности во круг начала координат на угол α радиан, где α – любое действительное число.

1. 1. Пусть α>0. Предположим, что точка, двигаясь поединичной окружности от точки Р против часовой стрелки, прошла путь длиной α (рис. 1). Конечную точку пути обозначим М.

В этом случае будем говорить, что точка М получена из точки Р поворотом вокруг начала координат на угол α радиан.

2. 2. Пусть α<0. В этом случае поворот на угол α радиан означает, что движение совершалось по часовой стрелке и точка прошла путь длинной (рис. 2).

Поворот на 0 рад означает, что точка остается на месте.

15. Вопрос: Определение синуса, косинуса, тангенса и котангенса угла. Основное тригонометрическое тождество.

Ответ:

Синус угла - это отношение противолежащего катета к гипотенузе;

Косинус угла - это отношение прилежащего катета к гипотенузе;

Тангенс угла - это отношение противолежащего катета к прилежащему;

Котангенс угла – это отношение прилежащего катета к противолежащему.

Основное тригонометрическое тождество:

16. Вопрос: Формулы сложения cos(a±b), sin(a±b), tg(a±b), cosa±cosb, sina±sinb

Ответ:

17. Вопрос: Формулы синуса, косинуса, тангенса двойного и половинного угла.

Ответ:

18. Вопрос: Формулы приведения, вывод, примеры.

Ответ:

19. Вопрос: Уравнения вида cos x = a, sin x = a, tg x = a. Общие виды решений и частные случаи.

Ответ:

Решение уравнения   sin x = a

Обычная форма  записи решения
Более удобная форма записи решения
Ограничения  на число a	В случае, когда  , уравнение решений не имеет

      Графическое обоснование решения уравнения   sin x = a  представлено на рисунке 1

Рис. 1

Частные случаи решения уравнений   sin x = a

Уравнение	Решение
sin x = – 1
sin x = 0
sin x = 1

Решение уравнения   cos x = a

Обычная форма  записи решения
Более удобная форма записи решения
Ограничения  на число a	В случае, когда  , уравнение решений не имеет

      Графическое обоснование решения уравнения   cos x = a  представлено на рисунке 2

Рис. 2

Частные случаи решения уравнений   cos x = a

Уравнение	Решение
cos x = – 1
cos x = 0
cos x = 1

Решение уравнения   tg x = a

Обычная форма  записи решения
Более удобная форма записи решения
Ограничения  на число a	Ограничений нет

      Графическое обоснование решения уравнения   tg x = a  представлено на рисунке 3

Рис. 3

Частные случаи решения уравнений   tg x = a

Уравнение	Решение
tg x = – 1
tg x = 0
tg x = 1

20(1). Вопрос: Определение производной, правила дифференцирования, примеры.

Ответ: Производная функции − одно из основных понятий математики, а в математическом анализе производная наряду с интегралом занимает центральное место. Процесс нахождения производной называется дифференцированием. Обратная операция − восстановление функции по известной производной − называется интегрированием.

Производная функции в некоторой точке характеризует скорость изменения функции в этой точке.

f′(x)=y′(x)=df/dx=dy/dx