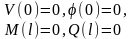Тема 7

Расчет прочности и жесткости простой балки

Лекция №13

Перемещения при изгибе

13.1 Характерные перемещения при изгибе.

13.2 Дифференциальное уравнение и система дифференциальных уравнений для функций перемещений и усилий.

13.3 Интегрирование дифференциального уравнения линии прогибов и определение произвольных постоянных.

13.4 Использование локальной системы координат при наличии нескольких участков интегрирования.

13.1 Характерные перемещения при изгибе.

Рассмотрим изгиб стержня в главной плоскости 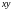(рис. 13.1,а). Как показывает опыт, реальные стержни, работающие в составе строительных конструкций, испытывают очень малые искривления. (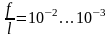 ). Основной вклад в создание этих деформаций вносят изгибающие моменты, вызывающие искривление каждого элемента балки длиной 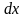на угол 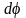(рис 13.1,б). Поперечные силы 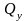создают у элементов деформации сдвига, которыми во многих случаях пренебрегают.

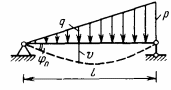
Рис.13.1 Перемещения при малых прогибах

Будем считать искривления малыми и учитывать лишь влияние изгибающих моментов. В этом случае неизвестной функцией, определяющей положение сечений балки в деформированном состоянии, является функция прогибов .

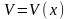Прогиб 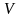- это перемещение центра тяжести сечения в направлении главной оси инерции сечения (на рис 13.1,а это ось у). Ось балки искривляется по кривой с уравнением , которую называют упругой линией или линией прогибов балки.

Кроме прогиба характерным перемещением произвольного поперечного сечения является его угол поворота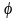 относительно оси .

Согласно гипотезе плоских сечений, каждое сечение при изгибе остается нормальным к оси изогнутого стержня, т.е. угол наклона касательной равен углу поворота сечения .

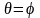Из аналитической геометрии известно, что тангенс угла наклона касательной к кривой равен первой производной от уравнения этой кривой.

(13.1)

Таким образом, из двух независимых функций и 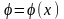основной является функция прогибов. Углы поворота получаются дифференцированием функции прогибов.

13.2 Дифференциальное уравнение и система дифференциальных уравнений для функций перемещений и усилий.

При выводе трехчленной формулы для нормальных напряжений было получено соотношение 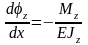(см. (9.14)), связывающие изгибающий момент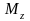 и создаваемый им угол искривления элемента стержня 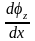(взаимный угол поворота торцов элемента – кривизна оси элемента).

Опуская индекс z в обозначениях с учетом (13.1) получим систему двух дифференциальных уравнений первого порядка

, .

(13.2)

Интегрирование системы уравнений (13.2) с учетом условий закрепления балки дает возможность найти функци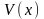и и .

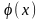Подстановка из второго уравнения системы (13.2) в первое дает дифференциальное уравнение второго порядка относительно функции прогиба

.

(13.3)

С учетом известных дифференциальных соотношений между поперечной силой и интенсивностью распределенной нагрузки (7.3) 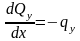, между изгибающим моментом и поперечной силой (7.4) 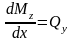, а также (13.2) получим:

, , , .

(13.4)

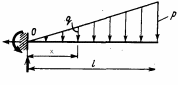
Интегрирование системы четырех обыкновенных дифференциальных уравнений первого порядка (13.4) выполняется с учетом граничных условий:

		(13.5)
		(13.6)
		(13.7)
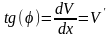
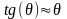
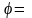
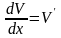
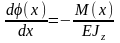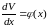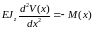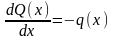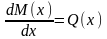