2.7 Перемещения и деформации.
Под действием внешних сил тело деформируется, т.е. изменяет свои размеры и форму (рис.2.9). Некоторая произвольная точка M переходит в новое положение M1. Полное перемещение MM1 будем разлагать на компоненты u, v, w , параллельные осям координат.
Рис 2.9 Полное перемещение точки и его компоненты.
Но перемещение данной точки еще не характеризует степень деформирования элемента материала у этой точки (пример: человек висит на канате, часть каната ниже захвата не деформируется).
Введем
понятие деформаций
в точке как количественную меру
деформирования материала в её окрестности.
Выделим
в окрестности т. М элементарный
параллелепипед
(рис.
2.10). За счет деформации длины его ребер
получат удлинение
.
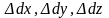Рис 2.10 Линейная и угловая деформации элемента материала.
Линейные
относительные деформации в точке
определятся так (
):
|
|
|
(2.5) |
Кроме
линейных деформаций возникают угловые
деформации
или углы сдвига, представляющие
малые изменения первоначально прямых
углов параллелепипеда (например,
в плоскости
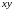это будет
).
Углы сдвига весьма малы и имеют порядок
.
Введенные относительные деформации в точке сведем в матрицу
.
(2.6)
Величины (2.6) количественно определяют деформацию материала в окрестности точки и составляют тензор деформаций.
2.8 Принцип суперпозиции.
Систему, в которой внутренние усилия, напряжения, деформации и перемещения прямо пропорциональны действующей нагрузке, называют линейно деформируемой (материал работает как линейно-упругий).
Кроме того, перемещения в конструкции должны быть достаточно малыми, чтобы изменения ее размеров и формы, возникающие вследствие деформации, можно было не учитывать в расчетной схеме (при составлении уравнений равновесия). Такие системы называются геометрически линейными.
Рис.2.11 Влияние перемещения узла на усилие в стержне
На
рис.2.11 показана геометрически нелинейная
система
.
Если пренебречь деформацией стержней
и считать
,
то
.
Принцип суперпозиции. Результат действия группы сил равен сумме (алгебраической или геометрической) результатов, полученных от действия каждой силы в отдельности.