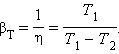2) Рассмотрим изохорный процесс.

V=const; m=const; A₁₂=0; dA=0.

(53.12)

– интегральная форма записи первого начала термодинамики для изохорного процесса.

(53.13)

– дифференциальная форма записи первого начала термодинамики для изохорного процесса.

Таким образом, в изохорном процессе всё полученное системой количество теплоты идёт на приращение внутренней энергии.

3) Рассмотрим изотермический процесс:

Т=const; m=const; ΔU=0, A₁₂≠0

(53.14)

- интегральная запись первого начала термодинамики для изотермического процесса.

В изотермическом процессе всё полученное системой количество теплоты идёт на совершение работы против внешних сил.

4) Адиабатный процесс.

По определению - адиабатный процесс происходит без теплообмена с окружающей средой: Q₁₂=0, тогда интегральная форма записи первого начала термодинамики для адиабатного процесса имеет вид:

(53.15)

Из соотношения (53.15) следует:

в адиабатном процессе работа совершается только за счёт убыли внутренней энергии.

Представим соотношение (53.15) в другом виде, выразив в выражении для внутренней энергии число степеней свободы через показатель адиабаты:

(53.16)

Теперь

(53.17)

А в дифференциальной форме записи первое начало термодинамики для адиабатного процесса имеет вид:

d¢Q=0, тогда

11. Закон распределения молекул по скоростям (распределение Максвелла)

функция распределения – доля молекул, приходящаяся на единичный интервал скоростей вблизи некоторого значения v, т.е. в интервале

Функция распределения – вероятность того, что скорость молекул лежит в единичном интервале вблизи некоторого значения v.

Распределение Максвелла:

m – масса молекулы

Распределение найдено с применением методов теории вероятности.

Свойства распределения Максвелла:

1. Кривая распределения имеет максимум, т.к. при малых значениях скорости v степенная функция v² растёт быстрее экспоненты, а при больших наоборот.

Экспонента в формуле распределения зависит от v²

2. При увеличении температуры Т максимум распределения смещается в сторону более высоких скоростей и понижается, т.к. площадь под кривой не меняется.

Условие нормировки

3. Доля молекул, приходящихся на единичный интервал скоростей вблизи v = 0 и v = ∞, равна нулю.

Связано это с тем, что в соответствии с теорией вероятности молекулы при столкновении не могут либо только отдавать, либо только получать энергию.

4. Доля молекул, обладающих строго определённым (точным) значением скорости, равна нулю.

5. Распределение Максвелла по скоростям справедливо для молекул не только идеального газа, но и для реального газа, жидкости, твёрдого тела.

6. Если систему молекул поместить в силовое поле, то это силовое поле не влияет на распределение молекул по скоростям.

12. Обратимые и необратимые процессы. Круговой процесс. Тепловые двигатели и холодильные машины.

Обратимые и необратимые процессы.

Процесс называют обратимым, если он протекает таким образом, что после окончания процесса он может быть проведен в обратном направлении через все те же промежуточные состояния, что и прямой процесс.

Свойством обратимости обладают только равновесные процессы

Процесс называется необратимым, если он протекает так, что после его окончания систему нельзя вернуть в начальное состояние через прежние промежуточные состояния.

Нельзя осуществить необратимый круговой процесс, чтобы нигде в окружающей среде не осталось никаких изменений.

Все реальные процессы протекают с конечной скоростью. Они сопровождаются трением, диффузией и теплообменом при конечной разности между температурами системы и внешней среды. Следовательно, все они неравновесны и необратимы. Всякий необратимый процесс в одном направлений (прямом) протекает самопроизвольно, а для осуществления его в обратном направлении так, чтобы система вернулась в первоначальное состояние, требуется компенсирующий процесс во внешних телах, в результате которого состояния этих тел .оказываются отличными от первоначальных. Например, процесс выравнивания температур двух соприкасающихся различно нагретых тел идет самопроизвольно, т. е. не связан с необходимостью одновременного существования каких-либо процессов в других (внешних), телах. Однако для осуществления обратного процесса увеличения разности температур тел до первоначальной нужны компенсирующие процессы во внешних телах, обусловливающие, например, работу холодильной машины

Круговой процесс

Круговым процессом, или циклом, называется такой процесс, в результате которого термодинамическое тело возвращается в исходное состояние.

В диаграммах состояния P, V и других круговые процессы изображается в виде замкнутых кривых. Это связано с тем, что в любой диаграмме два тождественных состояния (начало и конец кругового процесса) изображаются одной и той же точкой на плоскости.

Цикл, совершаемый идеальным газом, можно разбить на процессы:

расширения (1 – 2)

сжатия (2 – 1) газа

Работа расширения (1a2V₂V₁1) -

положительна (dV >0)

Работа сжатия (2b1V₁V₂2) -

отрицательна (dV < 0).

Работа, совершаемая за цикл, определяется площадью, охватываемой кривой

Если за цикл совершается положительная работа (цикл протекает по часовой стрелке), то он называется прямым Если за цикл совершается отрицательная работа (цикл протекает против часовой стрелки), то он называется обратным.

Рис. 1 Прямой цикл Рис. 2 Обратный цикл

Круговые процессы лежат в основе всех тепловых машин: двигателей внутреннего сгорания, паровых и газовых турбин, паровых и холодильных машин и т. д. В результате кругового процесса система возвращается в исходное состояние и, следовательно, полное изменение внутренней энергии газа равно нулю: dU = 0 Тогда первое начало термодинамики для кругового процесса

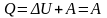
Если 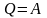т.о. работа, совершаемая за цикл, равна количеству полученной извне теплоты.

Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому

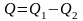
Q₁ – количество теплоты, полученное системой; Q₂ – количество теплоты, отданное системой

Тепловые двигатели и холодильные машины.

Тепловой двигатель – это периодически действующий двигатель, совершающий работу за счет полученной извне теплоты.

Термостатом называется термодинамическая система, которая может обмениваться теплотой с телами практически без изменения собственной температуры.

Рабочее тело – это тело, совершающее круговой процесс и обменивающееся энергией с другими телами.

Тепловой двигатель Холодильная машина

Принцип работы теплового двигателя от термостата с более высокой температурой T₁, называемого нагревателем, за цикл отнимается количество теплоты Q₁, а термостату с более низкой температурой T₂, называемому холодильником, за цикл передается количество теплоты Q₂, при этом совершается работа A = Q₁-Q₂. Термический КПД двигателя

 

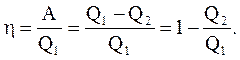
Чтобы КПД был равен единице, необходимо, чтобы Q₂ = 0, а это запрещено вторым началом термодинамики.

Процесс, обратный происходящему в тепловом двигателе, используется в холодильной машине: от термостата с более низкой температурой T₂ за цикл отнимается количество теплоты Q₂ и отдается термостату с более высокой температурой T₁>T₂. При этом   или 

Количество теплоты Q₁, отданное системой термостату T₁, больше количества теплоты Q₂, полученного от термостата T₂, на величину работы, совершенной над системой.

Эффективность холодильной машины характеризует холодильный коэффициент h’ – отношение отнятого от термостата с более низкой температурой количества теплоты Q₂ к работе A, которая затрачивается на приведение холодильной машины в действие:

 

Холодильные машины

Любой участок цикла Карно и весь цикл в целом может быть пройден в обоих направлениях. Обход цикла по часовой стрелке соответствует тепловому двигателю, когда полученное рабочим телом тепло частично превращается в полезную работу. Обход против часовой стрелки соответствует холодильной машине, когда некоторое количество теплоты отбирается от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Поэтому идеальное устройство, работающее по циклу Карно, называют обратимой тепловой машиной. В реальных холодильных машинах используются различные циклические процессы. Все холодильные циклы на диаграмме (p , V ) обходятся против часовой стрелки.

Устройство, работающее по холодильному циклу, может иметь двоякое предназначение. Если полезным эффектом является отбор некоторого количества тепла |Q ₂ | от охлаждаемых тел (например, от продуктов в камере холодильника), то такое устройство является обычным холодильником. Эффективность работы холодильника можно охарактеризовать отношением

т. е. эффективность работы холодильника – это количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. При таком определении β_х может быть и больше, и меньше единицы. Для обращенного цикла Карно

Если полезным эффектом является передача некоторого количества тепла |Q ₁ | нагреваемым телам (например, воздуху в помещении), то такое устройство называется тепловым насосом. Эффективность β_Т теплового насоса может быть определена как отношение

т. е. количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует:

|Q ₁ | > |A |,

Следовательно, β_Т всегда больше единицы. Для обращенного цикла Карно