Моделирование объекта регулирования расхода жидкости
Рисунок 3 - Схема трубопроводной сети
1- ось магистральных фланцев ИУ;
2- участок трубопроводной сети до ИУ;
3- исполнительное устройство;
4- участок трубопроводной сети после ИУ
Давление РН (в начале), больше давления РК (в конце). Расход зависит от перепада давления (РН-РК).
Запишем базовое соотношение: второй закон Ньютона:
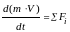, (3.1.27)
Где V- линейная скорость движения жидкости,
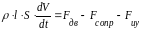, (3.1.28)
где
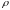- плотность жидкости,
- длина трубы,
S – внутреннее сечение трубы
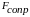- сила сопротивления,
которое обусловлено трением жидкости
о стенки трубы и на местных гидравлических
сопротивлениях
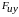- сила трения в ИУ.
Запишем функции зависимости параметров:
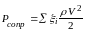, (3.1.29)
Перепад на местных сопротивлениях:
В динамике:
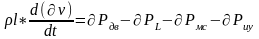(3.1.30)
При
t=0
и
=0
запишем зависимости
PL=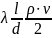
(5)
V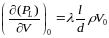
(3.1.31)
где
-
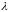коэффициент трения о стенки трубы.
Коэффициенты самовыравнивания:
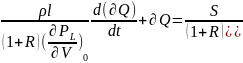
Тогда постоянная времени находится по формуле:
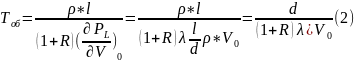
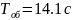
Где
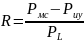(9)
Коу находится из расходной характеристики клапана.
В статике:
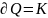оу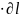
(3.1.32)
Зависимости расхода от степени открытия определяется расходной характеристикой:
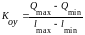. (3.1.33)
Коу=2.8
Получили две передаточные функции:
по каналу управления:
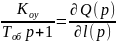(3.1.34)
по каналу возмущения:
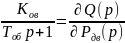(3.1.35)
Ков=3.52
Общее выражение передаточной функции имеет вид:
.
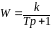(3.1.36)
Передаточная функция объекта регулирования расхода по каналу возмущения описывается уравнением:
W
=
(3.1.37)
а передаточная функция по каналу управления:
Wов
=
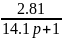(3.1.38)
3.2 Расчёт оптимальных настроек регулятора
Структурная схема одноконтурной системы регулирования расхода жидкости приведена на рисунке 3.3
Рисунок 4 – Структура АСР расхода жидкости
Объект регулирования является аппериодическим звеном 1-ого порядка с запаздыванием τз
Wоб
=
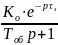(3.2.1)
Оптимальные настройки регулятора определяются по каналу возмущения исходные данные для расчёта взяты из предыдущего параграфа 3.1.
Ко= 3.2
Tоб= 14 сек
Q= 40 (м3/ч) = 0.011 (м3/сек)
Киу1= 1.1
Киу2= 2.4
DT= 0,097 (м) – диаметр трубопровода.
Время чистого транспортного запаздывания τз- это время движения жидкости по трубопроводу на расстояние от сужающего устройства до мембранного исполнительного механизма ( l).
Примем это расстояние равным 10м.
Тогда:
,
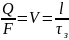где F-
сечение трубопровода в м3,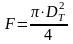
,V-
скорость движения жидкости.
τз=
Так как настройки регулятора рассчитываются по каналу возмущения, то обобщённый коэффициент усиления объекта Коб вычисляется как
Коб= Киу1ˑКоб
Таким образом, расчитанные значения коэффициентов передаточной функции объекта (1)
Коб= 3.52 Tоб= 14 сек τз= 7 сек
а сама передаточная функция принимает окончательный вид:
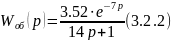
Для расчёта оптимальных настроек регулятора принимаем метод Кохена и Куна. Этот метод лучше всего подходит для расчёта настроек регулятора в нашем случае, кроме того метод графический, для чего необходимо получить кривую разгона объекта регулирования. Кривая разгона для одноёмкостного объекта вычисляется по уравнению (3):
где t- текущее время.
С учётом чистого запаздывания график кривой разгона имеет следующий вид:
Рисунок 5 - Теоретическая кривая разгона объекта регулирования.
Приведём график кривой разгона к виду, принятому в методе Кохена и Куна.
Рисунок 6 - Апроксимированная кривая разгона объекта регулирования.
Авторы
метода настройки пропорционально-интегрального
регулятора с передаточной функцией
Wрег=К+
предлагают
определять по эмпирическим формулам:
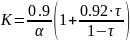
Где
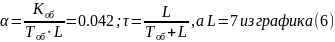
Для моего примитивного графика (рис. 6)
Подставив значения α и τ в уравнения (3.2.4), находим значения оптимальных настроек ПИ-регулятора
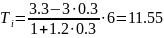
К=22.8 Ti=11.55 сек
Таким образом, получены оптимальные настройки К и Тi пропорционально-интегрального регулятора.