
Учебник Теория вероятности - Самойленко, Кузнецов
.pdf
|
|
|
Теория вероятностей |
x1 = k1 − np ; x2 = |
k2 − np ; Ф(х)= |
1 ∫e− |
t2 |
2 dt – функция Лапласа. |
|||
|
|
x |
|
np(1− p) |
np(1− p) |
2π 0 |
|
3.24. Интегральная теорема Лапласа предназначена для оценки вероятности того, что число появлений некоторого события при многократном повторении независимых опытов попадет в заданный диапазон. 3.25. Функция Лапласа имеет центральную симметрию относительно начала системы координат, поскольку является нечетной функцией. 3.26. Функция Лапласа от аргумента –6,7 равна 0,5, т.к. аргумент по модулю превышает значение 5. 3.27, а) 0,8882; б) 0,8944; в) 0,1056; г) 0,1512. 3.28. Наивероятнейшим числом наступления события А в n независимых опытах при одинаковой вероятности наступления события А в каждом из них называется число k0, которому соответствует
максимальная вероятность Рn(k), то есть число |
k0 |
|
|
3.29. |
= arg max{P(k )} . |
||||
|
|
k =1,n |
|
|
np-q ≤ k0 ≤ np+p. 3.30. Особенности двойного неравенства: значение правой части превышает значение левой ровно на единицу; k0 – целое число; внутри диапазона значений [np–q; np+p] может находиться только одно целое число, либо два – на его границах. 3.31. Определение k0 осуществляют в следующей последовательности. Сначала вычисляют величину np. Если np – целое число, то k0 = np. Если np – не целое число, определяют величину np+р. Если (np+р) – целое число, то существует два наивероятнейшего числа: k01=np+р и k02=k01–1. Если (np+р) – не целое число, то k0 – целое число в диапазоне [np–q; np + p]. 3.32, а) 3; б) 1 и 2;
в) 1.
4.1. Случайной называют величину, которая в результате опыта принимает заранее неизвестное значение. 4.2. Дискретными называют случайные величины, которые в результате опыта принимает значения из счетного множества (конечного или бесконечного). 4.3. Непрерывными называют случайные величины, которые в результате опыта принимает значения из непрерывного множества (ограниченного или неограниченного). 4.4. Закон распределения случайной величины – это соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями. 4.5. Существует две эффективные формы задания закона распределения дискретной случайной величины: ряд распределения и интегральная функция распределения. 4.6. Ряд распределения представляет собой таблицу, состоящую из двух строк и задающую закон распределения дискретной случайной величины. 4.7. Искомый ряд распределения:
xi |
0 |
1 |
2 |
pi |
1 / 4 |
1 / 2 |
1 / 4 |
170
Ответы
4.8. Искомый ряд распределения:
xi |
pi |
0 |
1 |
2 |
1 / 45 |
16 / 45 |
28 / 45 |
4.9. Интегральная функция распределения случайной величины X – это функция F(x), которая при каждом значении своего аргумента x численно равна вероятности того, что случайная величина X окажется меньше, чем значение аргумента. 4.10. Интегральная функция распределения случайной величины обладает следующими свойствами: интегральная функция от минус бесконечности равна нулю; интегральная функция от плюс бесконечности равна единице; интегральная функция – функция неубывающая. 4.11. Искомый ряд распределения:
xi |
0 |
1 |
pi |
q |
p |
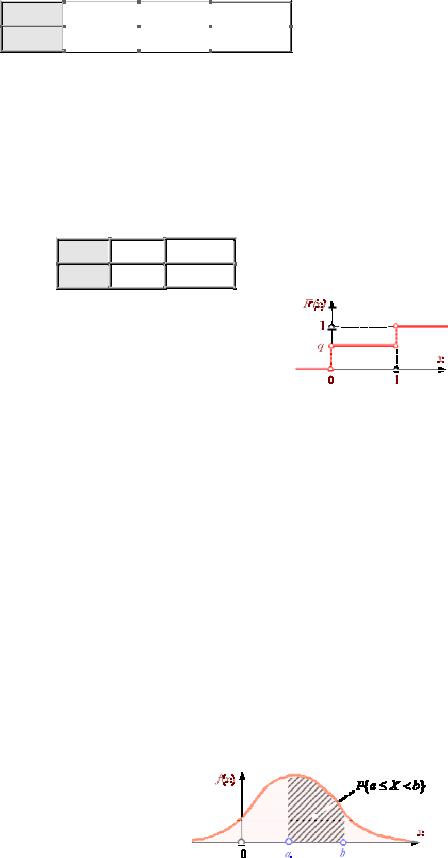
Здесь q = 1– р. Интегральная функция распределения:
4.12. P{a ≤ X < b}= F(b)− F(a). 4.13. Существует две эффективные формы задания закона распределения непрерывной случайной величины: интегральная функция распределения и плотность распределения вероятности. 4.14. Интегральная функция дискретной случайной величины – ступенчатая функция, т.е. скачкообразно возрастающая функция, а интегральная функция непрерывной случайной величины – монотонно возрастающая функция. 4.15. Вероятность конкретного значения непрерывной случайной величины равна нулю. 4.16. Плотностью распределения вероятности непрерывной случайной величины называется первая производная от интегральной функции
распределения. 4.17. F(x)= ∫x f (t)dt . 4.18. Интеграл в бесконечных
−∞
пределах от плотности распределения равен единице. 4.19. Плотность
распределения – функция неотрицательная. 4.20. P{a ≤ X < b}= b∫ f (x)dx .
a
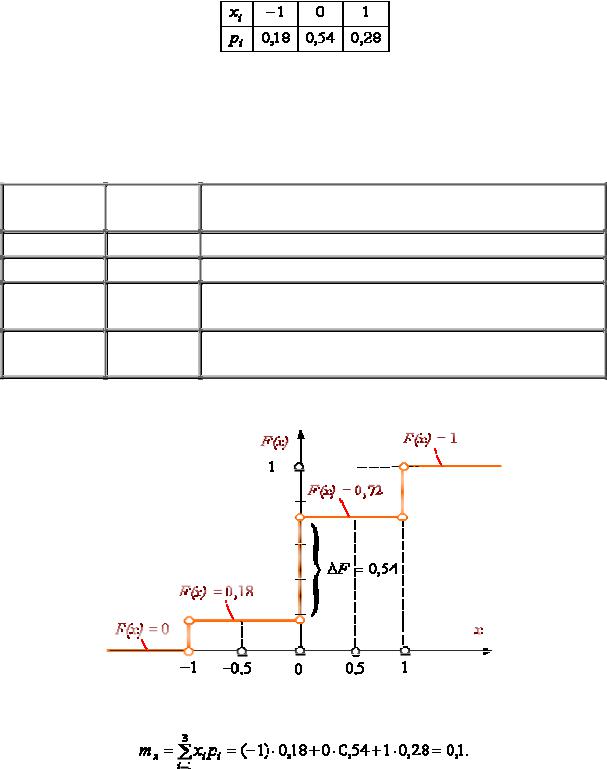
4.21. Вероятность попадания непрерывной случайной величины на заданный участок числовой оси (a, b) численно равна площади заштрихованной области на графике плотности распределения .
171

Теория вероятностей
4.22. Математическое ожидание, мода и медиана. 4.23. Математическое ожидание – это средневзвешенное по вероятностям значение случайной величины. 4.24. Математическое ожидание характеризует смещение значений случайной величины на числовой оси относительно начала
координат. 4.25. |
n |
4.26. |
mx = |
∞ |
4.27. Модой |
mx = ∑ xi pi . |
∫ x f (x)dx . |
||||
|
i=1 |
|
|
−∞ |
|
называют наиболее вероятное значение случайной величины. Медианой называют такое значение Ме случайной величины которого справедливо равенство P{X < Me}= P{X > Me}. 4.29. Нет.
Математическое ожидание равно 1,2. Мода равна 2. 4.31. Начальным моментом k-го порядка называют математическое ожидание k–й степени
n |
4.33. αk = |
∞ |
4.34. |
случайной величины. 4.32. αk = ∑ xik pi . |
∫ xk f (x)dx . |
||
i=1 |
|
−∞ |
|
Центрированной случайной величиной называют отклонение значения случайной величины от её математического ожидания. 4.355. Центральным моментом s-го порядка называют математическое ожидание
n |
(xi − mx ) |
s |
s-й степени центрированной случайной величины. 4.36. µs = ∑ |
pi . |
|
i=1 |
|
|
4.37. µs = ∞∫(x −mx )s f (x)dx . 4.38. Знак «=». 4.39. 0. 4.40. Начальный |
||
−∞ |
|
|
момент 2-го порядка случайной величины характеризует степень разброса случайной величины вокруг её математического ожидания, а также
смещение |
случайной |
величины на |
числовой оси относительно начала |
|
координат. |
4.41. α2 = |
n |
∞ |
4.43. |
М[X2] = ∑xi2 pi . |
4.42. α2 = М[X2] = ∫x2 f (x)dx . |
|||
|
|
i−1 |
−∞ |
|
Второй начальный момент используется для определения второго центрального момента. 4.44. Центральный момент 2-го порядка характеризует степень разброса случайной величины вокруг её математического ожидания. 4.45. Знак «=». 4.46. Dx =α2 −mx2 . 4.47.
Среднее квадратичное отклонение представляет собой квадратный корень из дисперсии. 4.48. Среднее квадратичное отклонение характеризует то же, что и дисперсия. 4.49. α 2 = 2,16 ; Dx = 0,72 ; σ x= 0,85. 4.50.
Построим сначала ряды распределения для случайных величин Х1 и Х2:
В построенных законах распределения вероятности промахов определяются как вероятности противоположных событий, соответственно: q1=1–p1=1–07=0,3; q2=1–p2=1–0,6=0,4. Полученные ряды распределения позволяют построить ряд распределения для случайной
172
Ответы
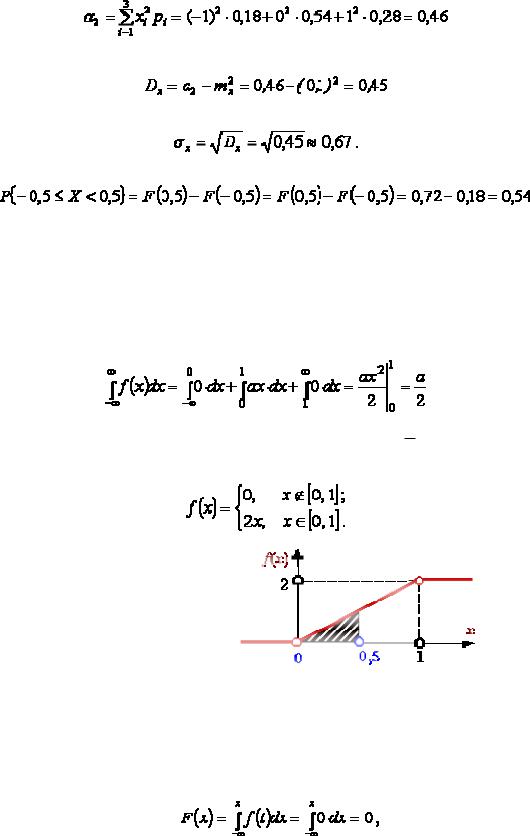
величины Х=Х1–Х2. Определим сначала возможные значения случайной величины Х и соответствующие вероятности: если Х1=0 и Х2=1 то Х=–1, a вероятность исхода q1*p2=0,18; если Х1=0 и Х2=0 или Х1=1 и Х2=1 то Х=0, a вероятность исхода q1*q2 + p1*p2 = 0,54; если Х1=1 и Х2=0 то Х=1, a вероятность исхода q1*p2 = 0,28. Искомый ряд распределения:
Ряд распределения позволяет построить таблицу и график интегральной функции распределения.
Табличное задание интегральной функции случайной величины Х
Индекс
диапазона
1
2
3
4
Диапазон
х
х≤ –1
–1 ≤ х<0
0 ≤ х<1
х>1
F(x)

 F(x) = P{X<x}= 0
F(x) = P{X<x}= 0

 F(x) = P{X<x}= P(X=–1) = 0,18
F(x) = P{X<x}= P(X=–1) = 0,18
F(x) = P{X<x}= P(X=–1) + P(X=0) = = 0,18 + 0,54 = 0,72
F(x) = P{X<x}= P(X=–1) + P(X=0) + P(X=1) = = 0,18 + 0,54 + 0,28 = 1
График интегральной функции:
Математическое ожидание определим по формуле (4.9)
173
Теория вероятностей
Для определения дисперсии Dx предварительно определим второй начальный момент α2 по формуле (4.15)
Теперь с помощью формулы связи (4.19) определим дисперсию
По формуле (4.20) найдем среднее квадратичное отклонение:
Вероятность P{–0,5 ≤X < 0,5} определим по формуле (4.2) :
Данную операцию целесообразно осуществлять с помощью графика F(x).
4.51. Прежде чем вычислять искомые величины, необходимо определить параметр а в заданной плотности распределения f(x). Для определения параметра воспользуемся 1-м свойством плотности распределения, согласно которому определенный интеграл в бесконечных пределах от плотности распределения равен единице. Возьмём интеграл:
Затем приравняем результат интегрирования единице: a2 =1. Откуда а = 2.
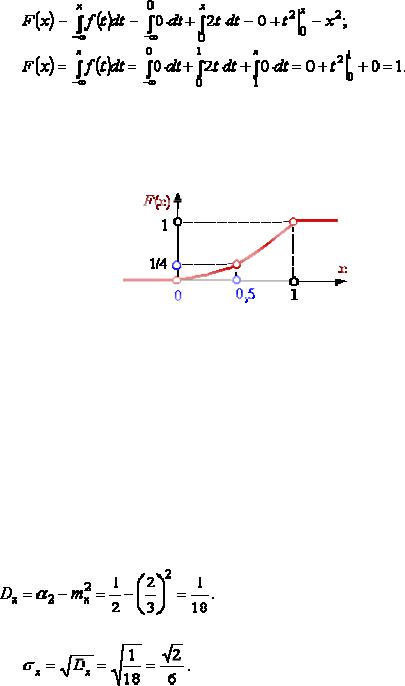
Итоговое выражение для плотности распределения имеет вид:
График f(x):
Для определения интегральной функции воспользуемся обратным преобразованием (4.5). Поскольку плотность распределения является кусочно непрерывной функцией, имеющей три диапазона с различным видом подынтегральной функции, то обратным преобразованием следует воспользоваться три раза:
для диапазона x < 0
174
Ответы
для диапазона 0 ≤ x ≤1
для диапазона х>1
|
0, |
если |
x ≤ 0; |
Таким образом, |
F(x)= x2 , |
если |
0 < x ≤1 |
|
|
если |
x >1. |
|
1, |
График интегральной функции F(x):
Для определения математического ожидания воспользуемся формулой
(4.10)
|
∞ |
0 |
1 |
∞ |
|
1 |
2x |
3 |
|
1 |
|
2 |
|
|
|
|
|
|
|
||||||||||
mx = |
∫x f (x)dx = |
∫x 0 |
dx +∫x 2x dx + ∫x 0 |
dx = 0 |
+2∫x2dx = |
|
|
|
|
= |
. |
|||
3 |
|
|
|
|
3 |
|||||||||
|
−∞ |
−∞ |
0 |
1 |
|
0 |
|
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
С целью дальнейшего определения дисперсии Dx определим сначала второй начальный момент:
|
∞ |
f (x)dx = |
0 |
1 |
∞ |
1 |
2x |
4 |
|
1 |
|
1 |
|
|
|
|
|
|
|||||||||||
α2 = |
∫x2 |
∫x2 |
0 dx +∫x2 |
2x dx + ∫x2 |
0 dx = 0 +2∫x3dx = |
|
|
|
|
= |
. |
|||
4 |
|
|
|
|
2 |
|||||||||
|
−∞ |
|
−∞ |
0 |
1 |
0 |
|
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Используя формулу (4.19), связывающую дисперсию с начальными моментами, определим Dx:
По формуле (4.20) найдем среднее квадратичное отклонение:
По определению медианы Р{X<Me} = P{X>Me}, но Р{X<Me} = F(Me) = 0,5. Следовательно, медиану можно найти из уравнения F(Me) = 0,5, что мы и сделаем:
175

Теория вероятностей
Последнюю искомую величину P{0 ≤ X<0,5} определим двумя способами:
Найденной вероятности на приведенном выше графике плотности распределения соответствует площадь заштрихованной области.
4.52. Третий центральный момент характеризует степень разброса случайной величины вокруг математического ожидания, а также степень
асимметрии её
n
= ∑(xi − mx )3 pi .
i=1
закона |
распределения. 4.53. |
µ3 = M [(X − mx )3 ]= |
|
4.54. |
µ3 = M [(X −mx )3 ]= ∞∫(x −mx )3 f (x)dx . |
4.55. |
|
|
−∞ |
|
|
Коэффициент асимметрии характеризует степени асимметрии закона распределения. Коэффициент асимметрии определяется по формуле
s = µ3 . 4.56. 0,144. 4.57. Четвертый центральный момент характеризует
σ x3
степень разброса случайной величины вокруг математического ожидания, а также степень островершинности её закона распределения. 4.58. Величина эксцесс характеризует степени островершинности закона распределения, заданного с помощью плотности распределения. Величина
эксцесс определяется по формуле E = |
µ4 |
−3 . |
|
σ 4 |
|||
|
|
||
|
x |
|
5.1. Cлучайная величина распределена по биномиальному закону, если её ряд распределения имеет вид:
xi |
0 |
1 |
. . . |
m |
. . . |
n |
pi |
(1-p)n |
np(1-p)n-1 |
. . . |
Cnm pm(1-p)n-m |
. . . |
pn |
|
|
|
|
|
|
|
5.2. Ряд распределения случайной биномиальной величины c параметрами распределения p=0,6 и n=4:
176
Ответы
|
xi |
|
0 |
1 |
|
2 |
3 |
|
4 |
|
|
pi |
|
0,0256 |
0,1536 |
0,3456 |
0,3456 |
|
0,1296 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5.3. М[X] = np. |
5.4. D[X] |
= np(1–p). |
5.5. |
σ x = Dx |
= np(1− p) . 5.6. |
|||||
k
P{k1 ≤ X ≤ k2 }= ∑2 Cni pi (1− p)n−i . 5.7. Случайным потоком событий
i=k1
называются события, следующие друг за другом в случайные моменты времени. 5.8. Простейшим потоком событий называется поток событий, обладающий тремя свойствами: стационарностью, ординарностью и отсутствием последействия. 5.9. Случайный поток событий называется стационарным, если вероятность попадания определенного числа событий на заданный временной участок зависит только от длины участка Т и не зависит от того, где на временной оси t расположен этот участок. 5.10. Случайный поток событий называется ординарным, если вероятность попадания двух и более событий на бесконечно малый участок несоизмеримо мала по сравнению с вероятностью попадания одного события на этот участок. 5.11. Случайный поток событий называется потоком без последействия, если вероятность попадания определенного числа событий на участок длиной Т не зависит от того, сколько событий попало на любой другой участок, не пересекающийся с ним. 5.12. Случайная величина распределена по закону Пуассона, если её ряд распределения имеет вид:
|
xi |
|
0 |
1 |
. . . |
m |
|
. . . |
|
|
pi |
|
е–а |
а е–а |
. . . |
(аm е–а)/m! |
|
. . . |
|
|
|
|
|
|
|
|
|
|
|
5.13. М[X] = а. |
5.14. D[X] = а. 5.15. σ x = |
Dx = a . |
5.16. Параметр а = |
||||||
=λТ = 4 блока . |
а) Р(X=10) = Р(X≤10) – Р(X≤9) = 0,00529 |
; б) Р(X>10) = |
||||||||||
= 1 – Р(X≤9) ; |
в) Р(X<10) |
= |
Р(X≤9). 5.17. |
Функция |
распределения |
|||||||
вероятности: P(X = k) = |
ak |
|
e−a |
= |
3k |
|
e−3 , |
k = 0,1,2,... |
а) Р(X≤2) |
= 1–Q(2,3) = 1– |
||
k! |
k! |
|||||||||||
|
|
|
|
|
|
|
|
|||||
0,577 = 0,423; |
б) Р(X>0) |
= |
Q(0,3). |
5.18. По условию математическое |
||||||||
ожидание числа вызовов за час mx = 30, тогда математическое ожидание числа вызовов за минуту mx = 30/60 = 0,5. Р(X≥2) = Р(X>1) = Q(1;0,5) =
0,0902. |
5.19. |
Параметр |
а = np = 1000*0,002 |
|
= |
2. |
Тогда |
P(X = 3) = |
||||||||||||
= |
a3 |
e−a = |
23 |
e−2 |
≈ 0,18 |
(1-й |
способ), или |
Р(X=3) |
|
= |
Q(2,2) – |
Q(3,2) = |
||||||||
|
3! |
|
||||||||||||||||||
3! |
|
|
|
|
|
|
|
|
|
5.20. |
Параметр а = np = |
|||||||||
= 0,323 |
– |
0,143 = |
0,18 |
(2-й способ). |
||||||||||||||||
= 100000*0,0001 = 10, P(X = 5) = |
a5 |
e−a = |
105 |
e−10 ≈ |
0,1029 . |
5.21. Параметр |
||||||||||||||
|
5! |
|||||||||||||||||||
|
|
|
|
|
|
|
5! |
|
|
|
|
|
|
|
|
|
|
|
||
а = np = 200*0,01 = 2 . Тогда P(X = 4) = |
a4 |
|
e−a = |
24 |
e−2 |
≈ 0,09 |
(1-й способ), или |
|||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
4! |
|
4! |
|
|
|
|
|
|
|||||
177

Теория вероятностей
Р( X = 4 ) =Q(3,2) – Q(4,2) = 0,142 – 0,052 = 0,09 (2-й способ). 5.22.
Параметр а = np = 500 * 0,002 = 1. |
а) |
|
P(X = 3) = |
a3 |
e−a |
= |
13 |
e−1 ≈ 0,0613 |
(1-й |
||||||||||||||||||||
3! |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3! |
|
|
|
|||||
способ), или Р(X=3) = Q(2,1)–Q(3,1) = 0,0803–0,0190 = 0,0613 (2-й способ); |
|||||||||||||||||||||||||||||
б) P(X = 0) + P(X = 1) + P(X = 2) = |
10 |
e−1 + |
11 |
e−1 + |
12 |
e−1 = |
5 |
e−1 ≈ 0,9197 (1-й способ), |
|||||||||||||||||||||
|
|
2! |
2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
0! |
|
1! |
|
|
|
|
|
|
|
|
|
|
в) Р(X>3) = |
|||||||||
или (2-й способ) Р(X<3) = 1 – Q(2,1) =1 – 0,0803 = 0,9197; |
|||||||||||||||||||||||||||||
=Q(3,1) = 0,19; г) Р(X>0) = Q(0,1) = 0,632. |
5.23. Заданную по условию |
||||||||||||||||||||||||||||
вероятность можно выразить через уравнение 0,98 = 1 – Р( X = 0 ), или |
|||||||||||||||||||||||||||||
|
a0 |
−a |
|
-a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0,02 = |
|
e |
|
. Откуда е |
= 0,02 и а ≈ 4 . Таким образом, среднее число |
||||||||||||||||||||||||
0! |
|
||||||||||||||||||||||||||||
отказов равно 4. 5.24. Непрерывная случайная величина распределена по |
|||||||||||||||||||||||||||||
равномерному |
закону, |
если ее |
плотность |
распределения |
имеет |
вид: |
|||||||||||||||||||||||
f (x)= 0 , |
|
x |
[a,b]; |
5.25. |
|
Интегральная |
|
|
|
|
функция |
равномерно |
|||||||||||||||||
|
c , |
|
x [a,b]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 , |
|
|
|
|
x < a ; |
|
|
|||||||
распределенной величины имеет вид: |
|
|
x |
− a |
|
|
|
|
|
|
|
5.26. М[X]= |
|||||||||||||||||
F(x) = |
|
|
|
|
, |
|
a ≤ x ≤ b ; |
||||||||||||||||||||||
|
− a |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
x > b . |
|
|
||||||||
|
|
|
|
|
|
|
(b − a)2 . |
|
|
1 , |
|
|
|
|
|
|
|||||||||||||
= (a+b)/2. |
|
5.27. Dx |
= |
5.28. |
|
|
σ x |
= |
|
Dx |
= (b − a) |
3 . |
5.29. |
||||||||||||||||
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|||||
[α, β] [a,b] |
|
P{α ≤ X < β |
}= |
β −α |
. 5.30, а) 1/4; |
б) 1. |
5.31. 3/5. 5.32. 1/3. |
||||||||||||||||||||||
b − a |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5.33. 3. 5.34. Случайная величина распределена по показательному
закону, |
если |
ее |
плотность |
распределения |
имеет |
вид: |
0 , |
t < 0 ; |
|
λ – интенсивность событий, |
т.е. количество |
||
f (t)= λ e−λt , t ≥ 0 , где |
||||||
|
|
|
|
|
|
|
событий в единицу времени. 5.35. Интегральная функция случайной
величины, |
распределенной |
по |
показательному закону, |
|
имеет |
вид |
|||||||||||||||
|
|
0 , |
|
|
t < 0 ; |
5.36. mx = |
1 |
|
. 5.37. Dх = |
|
1 |
. 5.38. σ x = Dx = |
1 = |
||||||||
F(t) = |
|
|
|
|
|
|
|||||||||||||||
|
|
|
t ≥ 0 . |
λ |
|
||||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
1−e−λt , |
|
|
|
|
λ2 |
|
|
|
λ2 |
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−5x |
, |
при |
х ≥ 0; |
||
= |
. |
5.39. |
P{a ≤ T < b}= e−λa −e−λb . |
5.40. |
|
f (x)= 5e |
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
0 , |
|
|
при |
х < 0. |
|||
|
|
|
−e |
−5x |
|
|
х ≥ 0; |
5.41. |
Определим |
|
интегральную |
функцию: |
|||||||||
F(x)= 1 |
|
, |
при |
|
|||||||||||||||||
|
|
0 , |
|
|
при |
х < 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 , |
|
|
x < 0 ; |
|
|
|
|
|
|
P{0 ≤ X < mx }= P{0 ≤ X |
|
1 |
}= |
||||||
F(x) = 1 |
−e−λx , |
x ≥ 0 . Искомая вероятность: |
|
< |
|||||||||||||||||
|
λ |
||||||||||||||||||||
|
|
|
|
|
|
|
|
5.42. |
P{0,13 ≤ X < 0,7}= e−3 0,13 −e−3 0,7 ≈ 0,555 . |
||||||||||||
= e−λ a − e−µ λ |
=1− e−1 ≈ 0,632. |
||||||||||||||||||||
178
Ответы
5.43. |
0,2. |
|
5.44. |
Определим |
|
константу |
с: |
∞ |
f (x) dx =1; |
∞ |
||||||||||||||||
|
|
∫ |
∫ f (x) dx = |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
−∞ |
= ∫0 |
0 dx +∞∫c e−λ x |
|
0∞ = 0 − |
c |
= |
c |
; |
|
c |
=1. |
Откуда |
|
c = λ |
. |
5.45. |
Случайная |
||||||||||
|
|
|||||||||||||||||||||||||
|
− λ |
|
|
λ |
|
|||||||||||||||||||||
−∞ |
0 |
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
величина |
распределена по |
нормальному |
закону, |
если |
ее |
плотность |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
f (x)= |
|
1 |
|
e− |
(x−m)2 |
|
|
|
|
|
|
|
|||
распределения |
имеет вид: |
σ |
|
|
2σ 2 |
|
, |
где |
σ |
и m – |
параметры |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
||
распределения. |
5.46. Интегральная функция нормально распределенной |
|||||||||||||||||||||||||
случайной |
величины |
|
имеет |
|
вид: |
|
F(x) = |
|
1 |
x |
−(t−m)2 |
5.47. |
||||||||||||||
|
|
|
σ |
∫e 2σ 2 |
dt . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
−∞ |
|
|
|
|
Математическое ожидание равно параметру m; среднее квадратичное отклонение – параметру σ; дисперсия – σ2. 5.48. µs = (s −1)µs−2σ 2 . 5.49. Коэффициент асимметрии нормально распределенной случайной
величины равен нулю. |
|
5.50. Коэффициент островершинности нормально |
|||||||||||||||||||||||||||||||||
распределенной |
|
|
случайной |
|
величины |
|
равен |
|
нулю. |
5.51. |
|||||||||||||||||||||||||
|
|
|
b |
− m |
|
a |
− m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
P{a ≤ |
X < b}= Ф |
|
|
|
−Ф |
|
|
|
|
|
. |
|
|
|
|
5.52. |
|
mx=5, |
|
Dx=25. |
5.53. |
||||||||||||||
|
σ |
|
σ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
b − m |
|
|
a − m |
25 − 20 |
|
15 − 20 |
|
|
|
|
|||||||||||||||||||||
P{15 < X < 25}= Ф |
|
|
|
|
−Ф |
|
|
|
|
|
|
|
= Ф |
|
|
|
|
|
|
−Ф |
|
|
|
|
= 2Ф(1)≈ 0,6826 . |
||||||||||
|
σ |
|
|
|
σ |
|
|
5 |
|
|
5 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
b − m |
|
|
|
a − m |
|
10 − |
0 |
10 |
− 0 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
5.54. |
P{ |
X |
<10}= Ф |
|
|
|
|
|
|
−Ф |
|
|
|
= Ф |
|
|
|
|
−Ф |
|
|
|
= 2Ф(0,5) |
≈ 0,383. |
|||||||||||
|
σ |
|
|
σ |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
20 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
d |
1 |
+ d |
2 |
|
|
|
|
|
||
|
|
|
|
d2 |
− |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
||||||||
5.55. |
P =1− P{d1 |
< D < d2 |
}=1− Ф |
|
|
|
|
|
|
|
|
− |
Ф |
|||
|
d2 − d1 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
=1−[Ф(2)−Ф(− 2)]=1− 2Ф(2)=1− 2 0,4772 = 0,0456 . |
|
|||||||||||||||
d1 − |
d |
1 |
+ d |
2 |
|
|
|
||
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
= |
|
|
d2 − d1 |
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5.56. |
|
Если |
случайная |
||||||
величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднеквадратичного отклонения. 5.57. Если независимые случайные величины ui распределены по стандартному нормальному закону, т.е. по
нормальному |
закону |
с параметрами m = 0 и σ = 1, тогда случайная |
величина χ2 |
n |
|
= ∑ui2 распределена по закону хи-квадрат с числом степеней |
||
|
i=1 |
5.58. Если случайная величина u распределена по |
свободы k, равным n. |
||
стандартному нормальному закону, а случайная величина v распределена по закону хи-квадрат со степенью свободы k и не зависит от u, тогда
случайная величина t = |
u |
распределена по закону Стьюдента с числом |
|
v k |
|
степеней свободы k. 5.59. Если независимые случайные величины u и v
179
