Примерный перечень вопросов для подготовки к экзамену по дисциплине «Математика и правовая информатика»

1. Элементы математики Свойства операций и отношений.

2. Элементы теории множеств.

3. Элементы математической логики.

4. Элементы теории вероятностей. Вероятность события.

5. Классический подход к определению вероятностей.

6. Основные принципы и формулы комбинаторики.

7. Аксиоматический подход к определению вероятностей. Аксиомы теории вероятностей.

8. Формула полной вероятности.

9. Формула гипотез (Байеса).

10. Ряд и многоугольник распределения дискретных случайных величин.

11. Мода и медиана случайной величины.

12. Гипергеометрическое распределение.

13. Биномиальное распределение.

14. Среднее, дисперсия, среднеквадратическое отклонение случайной величины.

15. Элементы математической статистики. Выборочный метод.

16. Ряды распределения. Статистическая группировка и сводка данных.

17. Графическое представление статистических данных.

18. Выборочные среднее, дисперсия.

19. Выборочные мода, медиана.

20. Ошибка репрезентативности выборки.

21. Определение необходимого объема выборки.

22. Абсолютные и относительные величины.

23. Среднее арифметическое, гармоническое, геометрическое.

24. Статистическая зависимость. Коэффициент корреляции.

25. Элементы теории графов.

26. Задача определения пропускной способности сети.

27. Задача сетевого планирования.

28. Алгоритм и его свойства.

29. Модель. Классификация моделей.

30. Интерполяционная модель функции.

31. Модель и алгоритм численного решения уравнений.

32. Регрессионная модель. Функция регрессии. Линейная регрессия. Прогнозирование.

33. Сущность правовой информатики и общенаучные предпосылки ее формирования

34. Элементы общей теории систем, системного анализа.

35. Системы с управлением. Классификация систем с управлением.

36. Элементы исследования операций и теории принятия решений.

37. Оценка эффективности решений.

38. Предмет и задачи правовой информатики

39. Понятие, виды и источники правовой информации

40. Виды информационных задач решаемых в юридической деятельности

41. Классификация информационных систем используемых в юридической деятельности

42. Компьютерные системы автоматизации проведения криминалистических исследований и экспертиз

43. Автоматизация учета лиц по признакам внешности

44. Автоматизация дактилоскопической регистрации

45. Информационно – поисковые правовые системы

46. Автоматизированные информационно-поисковые системы, используемые в органах внутренних дел

47. Основные правила функционирования экспертных систем используемых в юридической деятельности

48. Методы и способы совершения компьютерных преступлений

49. Правовые методы защиты информации в компьютерных системах

50. Организационно - технические методы защиты информации в компьютерных системах

51. Программные методы защиты информации в компьютерных системах

52. Криптографические методы защиты информации

53. Криптография с открытым ключом

54. Криптография с закрытым ключом

55. Понятие электронной подписи

56. Информационная основа правотворческой деятельности

57. Информатизация деятельности Государственной Думы

58. Информатизация деятельности Совета Федерации

59. Использование автоматизированных обучающих систем в юридических вузах

60. Проблемы федерального информационного права 

1. Элементы математики Свойства операций и отношений.

Элементы:	Числовая алгебра	Право
1. система объектов	Числа	Человек, государство, собственность, ...
2. отношения между объектами	>, <, =, ...	родства, гражданство, к собственнос­ти (собственник, владелец,...), ...
3. операции над объектами	+ – */ ...	купли-продажи,...

Часто абстрактные объекты в математике обозначаются именами. Например, в геометрии точки обозначаются прописными латинскими буквами A, B, C,...; имена отрезков образуются из имен концов отрезков – AB, CD,...., числовые значения длин отрезков представляются строчными латинскими буквами – a, b, c,... В числовой алгебре числа также могут заменяться именами: Вес = Рост – 100, a² + b² = c², y < x². Имена могут содержать и цифры, например, индексы: A₁, x₁₂..

В математике операции могут удовлетворять свойствам (на примере сложения и умножения чисел, для абстрактных сложения и умножения эти операции могут и называться не так):

a + b = b + a коммутативность

a(bc) = (ab)c ассоциативность

a(b + c) = ab + ac дистрибутивность (двух операций).

В числовой алгебре некоммутативными являются операции «/» и «–», они же не ассоциативны.

Отношения между объектами также могут обладать определенными свойствами.

Из a ▪ b и b ▪ c следует a ▪ c свойство транзитивности.

Например, в числовой алгебре:

из a < b и b < c следует a < c;

из a = b и b = c следует a = c

Свойство справедливо не для всех отношений. Например, отношение «является противоположным» не транзитивно. На множестве людей отношения «старше чем», «выше» обладают свойством транзитивности, а «является отцом» – нет.

2. Элементы теории множеств.

Под множеством мы будем понимать такой набор, группу, коллекцию элементов, обладающих каким-либо общим для них всех свойством или признаком.

Множества обозначим А, В, С…, а элементы множеств а, b, с…, используя латинский алфавит.

Можно сделать такую запись определения множества:

, где

“ ” – принадлежит;

“=>“ – следовательно; 

“ø” – пустое множество, т.е. не содержащее ни одного элемента.

Два множества будем называть равными, если они состоят из одних и тех же элементов

Например:

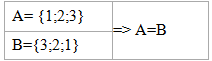
Если любой элемент из множества А принадлежит и множеству В, то говорят, что множество А включено в множество В, или множество А является подмножеством множества В, или А является частью В, т.е. если  , то  , где “С” знак подмножества или включения.

Графически это выглядит так (рис.1):

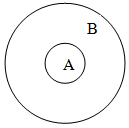
(рис.1)

Можно дать другое определение равных множеств. Два множества называются равными, если они являются взаимными подмножествами.

Рассмотрим операции над множествами и их графическую иллюстрацию (рис.2).

Объединением множеств А и В называется множество С, образованное всеми элементами, которые принадлежат хотя бы одному из множеств А или В. Слова “или” ключевое в понимании элементов входящих в объединение множеств.

Это определение можно записать с помощью обозначений:

А υ В, где   

где “ υ ” – знак объединения,

“ / ” – заменяет слова ”таких что“

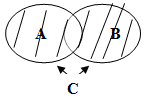
(рис.2)

Пресечение двух множеств А и В называется множество С, образованное всеми элементами, которые принадлежат и множеству А, и множеству В. Здесь уже ключевое слово “и”. Запишем коротко:

А ∩ В = С, где 

“∩“ – знак пересечения. (рис.3)

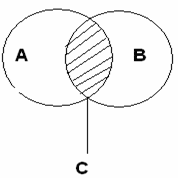
(рис.3)

Обозначим буквой Е основное или универсальное множество, где   A С Е (“ ”- любо число), т.е. А  Е = Е; А Е =А

Множество всех элементов универсального множества Е, не принадлежащих множеству А называется дополнением множества А до Е и обозначается ĀЕили Ā (рис.4)

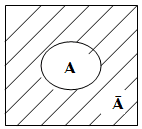Е

(рис.4)

Примерами для понимания этих понятий являются свойства:

_

А  Ā=Е                      Ø = Е             Е Ā=Ā

_

А ∩ Ā= Ø                 Ē = Ø             (Ā)=А

Свойства дополнения имеют свойства двойственности:

________ _ _

А В = А∩В

________ _ _

А В = АUВ

Введем еще одно понятие – это мощность множества.

Для конечного множества А через m (A) обозначим число элементов в множестве А.

Из определение следуют свойства:

m (A) + m (Ā) = m (E)

А = В => m(A) = m(B)

Для любых конечных множеств справедливы так же утверждения:

m (A B) =m (A) + m (В) – m (А∩В)

m (A∩B) = m (A) + m (В) – m (А В)

m (A B C) = m (A) + m (В) + m (С)– m (А∩В) - m (А∩С) – m (В∩С) – m (А∩В∩С).