Национальный исследовательский институт

Московский Энергетический Институт (Технический Университет)

Институт автоматики и вычислительной техники

Кафедра Прикладной математики

Лабораторная работа №4

по дисциплине «Параллельные системы и параллельное программирование»

тема: «Поиск минимального оставного дерева с использованием нитевого распараллеливания.»

Выполнил:

Машеров Д.Е.

А-13-08

Москва

2012 г.

Постановка задачи

Дана граф, требуется найти минимальное оставное дерева этого графа.

Охватывающим деревом (или остовом ) неориентированного графа G называется подграф T графа G, который является деревом и содержит все вершины из G. Определив вес подграфа для взвешенного графа как сумму весов входящих в подграф дуг, под минимально охватывающим деревом (МОД) T понимается охватывающее дерево минимального веса.

Последовательный алгоритм.

Используется алгоритм Прима.

Алгоритм начинает работу с произвольной вершины графа, выбираемой в качестве корня дерева, и в ходе последовательно выполняемых итераций расширяет конструируемое дерево до МОД. Пусть есть множество вершин, уже включенных алгоритмом в МОД, а величины , 1<= <=n, характеризуют дуги минимальной длины от вершин, еще не включенных в дерево, до множества , т.е.

(если для какой-либо вершины не существует ни одной дуги в , значение устанавливается равным ). В начале работы алгоритма выбирается корневая вершина МОД s и полагается 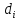={s}, =0.

Действия, выполняемые на каждой итерации алгоритма Прима, состоят в следующем:

• определяются значения величин di для всех вершин, еще не включенных в состав МОД;

• выбирается вершина t графа G, имеющая дугу минимального веса до множества ;

• вершина t включается в .

После выполнения n-1 итерации метода МОД будет сформировано. Вес этого дерева может быть получен при помощи выражения

Параллельный алгоритм.

Итерации метода должны выполняться последовательно и, тем самым, не могут быть распараллелены. С другой стороны, выполняемые на каждой итерации алгоритма действия являются независимыми и могут реализовываться одновременно.

Каждому потоку сопоставляется свой набор вершин графа.

На каждой итерации потоки находят вершину t и дугу на своем наборе вершин. После чего веса этих дуг сравниваются и находится дуга с минимальным весом уже во всем графе. Вершина, инцидентая найденной дуге, включается в множество .

Результаты вычислительного эксперимента

1. Количество вершин графа: 5 000

Число исполнителей	Время решения, секунд	Ускорение
1	347,497
2	174,977	1,99
3	118,731	2,93
4	95,798	3,63
5	94,552	3,68
6	81,686	4,25
7	71,231	4,88
8	64,493	5,39

2. Количество вершин графа: 10 000

Число исполнителей	Время решения	Ускорение
1	2638,806
2	1332,934	1,98
3	894,642	2,95
4	713,098	3,70
5	738,135	3,57
6	629,8	4,19
7	557,38	4,73
8	496,1	5,32