Национальный исследовательский институт

Московский Энергетический Институт (Технический Университет)

Институт автоматики и вычислительной техники

Кафедра Прикладной математики

Лабораторная работа №4

по дисциплине:

Параллельные системы

тема: «Задачи на графах»

вариант №5 – «Поиск автоморфизмов графа»

Выполнил:

Бочаров Иван Андреевич

Проверил:

Панков Николай Александрович

Москва

2012 г.

Введение

Дадим определение основному понятию, используемому в данной работе – понятию автоморфизма графа. Сперва рассмотрим неориентированный граф без петель.

Автоморфизм графа – произвольная подстановка на множестве вершин графа, сохраняющая отношение смежности, т.е. такова, что образы и вершин и смежны тогда и только тогда, когда смежны сами вершины u и v. Следует заметить, что очевидным образом это определение можно распространить на случай взвешенного ориентированного графа без петель – перестановка помимо отношения смежности должна сохранять веса рёбер между смежными вершинами.

Известно, что множество автоморфизмов графа образует группу с операцией композиции в качестве операции умножения.

Очевидно, что каждый граф имеет хотя бы один автоморфизм – тривиальную подстановку 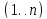. По этой причине для нас интерес представляют только нетривиальные автоморфизмы. Граф, для которого единственный возможный автоморфизм – это тождественное отображение, называется асимметрическим.

Метод решения

На данный момент не существует эффективного алгоритма поиска автоморфизмов графа. Все имеющиеся на сегодняшний день алгоритмы являются модификациями полного перебора (метод ветвей и границ и т.п.).

В данной работе используется полный перебор. Граф представляется матрицей смежности (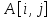– вес ребра из вершины в вершину). Для каждой нити параметром служит структура, несущая в себе информацию о числе подстановок, которое необходимо проверить, и об индексе перестановки, с которой нить должна начинать проверку на принадлежность к группе автоморфизмов графа. Также в поля этой структуры записывается результат – количество автоморфизмов, принадлежащих подмножеству множества подстановок, проверенных нитью, и их индексы.

При запуске нити по индексу определяется начальная перестановка, а затем в цикле проверяются все перестановки. Следует заметить, что перестановки упорядочены в лексикографическом порядке.

Результаты

Основные результаты были получены при тестировании разработанной программы на так называемых полных графах. Очевидно, что в полных графах группа автоморфизмов графа совпадает с множеством всех подстановок графа и имеет мощность , где – количество вершин графа. В связи с так называемым комбинаторным взрывом решение задачи поиска автоморфизмов графа может занимать значительное время.

Для каждого графа и количества нитей время было измерено 5 раз и в качестве конечного значения была выбрана медиана полученного множества.

Испытания проводились на стенде со следующей конфигурацией:

CPU: Intel Core i5 2500 МГц Ivy Bridge (3210M)

Количество ядер: 2 физических, 4 виртуальных

Кэш: 3 Mb L2 (L3) Cache

RAM: 4096 Мб DDR3-1600МГц

ОС: MS Windows 7 Home Basic x64

Таблица результатов (время в секундах):

Число нитей/Размер графа	7	8	9	10	11	12	ТГ,n=11
1	0,016	0,234	2,496	31,278	458,781	6889,355	3,898
2	0,015	0,124	1,357	17,862	288,803	4175,366	2,19
3	0,015	0,124	1,185	14,415	236,15	3414,605	1,946
4	0,015	0,093	1,061	12,916	220,647	3191,22	1,804
5	0,016	0,11	1,123	13,915	228,653		1,877
6	0,015	0,094	1,06	12,854	224,826		1,925
Число автоморфизмов	5040	40320	362880	3628800	39916800	479001600	1152

Ускорение

Число нитей/Размер графа	7	8	9	10	11	12	ТГ,n=11
2	1,067	1,887	1,839	1,751	1,589	1,650	1,780
3	1,067	1,887	2,106	2,170	1,943	2,018	2,003
4	1,067	2,516	2,352	2,422	2,079	2,159	2,161
5	1,000	2,127	2,223	2,248	2,006		2,077
6	1,067	2,489	2,355	2,433	2,041		2,025