Вопрос 16 Геометрический смысл частной произв. И диф-ла

z=f(x;y) и пусть например она имеет в т. (x_o;y_o) частн. произв. , где α согласно геометр. смыслу пр-ной одной переменной явл. углом наклона касательной к графику этой ф-ции, т.е. кривой z=f(x;y), y₌ y_o

Диф-л ф-ции в т. (x_o;y_o) означает что (

∆x=x-x_o; ∆y=y-y_o; ∆z=z-z_o

1. Плоскость опред. ур-нием z-z_o= ₎ называется касательной. П поверхности z=f(x;y) в т. (x_o;y_o;z_o) Обозначим апликату этой плос-ти через z_кас : ₎ , тогда z - = ( , а

нормаль:

2. Ур-е касат. плоскости и нормали к пов-ти, заданной неявно

кас. пл-ть:

нормаль:

Вопрос 17 Градиент, производная по направлению

Пусть задано направление (вектор) , функция и точка ,

t = раст. от M до M_o(x,y,z) Тогда производной по направлению в точке называется . Обозначение: . При этом .

Вектор с коорд. - градиент ф-ции f и обозн. , то .

Вопрос 18 Частные производные и диф-лы высших порядков

Част. производные 1-ого порядка также в свою очередь явл. ф-цией=>

z=f(x,y) f_xx’’(x_o,y_o)= ; f_yy’’(x_o,y_o)= ; f_yx’’(x_o,y_o)= ; f_xy’’(x_o,y_o) =

Производные f_xx’’ , f_yy’’ , f_yx’’ , f_xy’’ ­– частные производные 2 порядка. Аналог. находятся и более высших порядков.

Теорема о равенстве смешанных производных: Пусть в некоторой окрестности точки у функции и , причём обе эти функции непрерывны в точке . Тогда (или f_xy’’(x_o,y_o) = f_yx’’(x_o,y_o))

Док-во: Докажем, что

Замечание: оба выраж сост. из одних эл-тов слагаемых, значит . Преобразуем выраж (*) используя ф-лу конечного приращ. Лагранжа. Рассм. ф-цию . Выразим (*) с учётом этого

, где

Используя аналог. утверждение для (**) получаем , где и

Т.к. , то

; Если и , то . Устремим и . Тогда f_xy’’(x_o,y_o) = f_yx’’(x_o,y_o)

Диф-лы высших порядков для ф-ции y=f(x₁,x₂…x_n) диф-л записывается как

. Зафиксируем знач

Вопрос 19 Формула Тейлора для ф-ций мн. Переменных

Пусть в некоторой окрестности точки функция и все её частные производные до m+1-го порядка включительно существуют и непрерывны. Тогда для и удовлетв. условиям ф-ла: 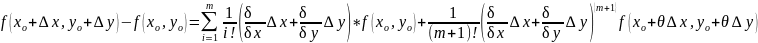– фор-ма Тейлора от ф-ции f(x,y) в т. (x_o,x_o) с ост. членом в форме Лагранжа.

- фор-ма Тейлора от ф-ции f(x,y) в т. (x_o,x_o) с ост. членом в форме Пиано. Используя понятие диф-ла высших порядков:

Вопрос 20 Экстремум ф-ции многих переменных

Необходимое условие экстремума: Пусть функция определена на некот. мн-ве Е, которое содержит точка локального min (max) ф-ции f(x) на мн-ве E, если сущ. нек. окр. т. , для всех x из которой выполн. нер-во

Если при этом при 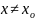, то т. строгий локальн. min (max)

Пусть в точке у функции экстремум и в точке существует частные производные . Тогда .

Пусть существует . Т.к. , где . Т.к. у в точке экстремум, то будет .

Точка, в кот. все частн. произв. сущ. и = 0 – критическая (стационарная) т. ф-ции

Достаточное условие экстремума:

Предполож, что ф-ция f(M)=f(x₁,x₂,x_n) в крит. т.M^o имеет непрерыв. частн. производ. 2-ого порядка. Расм. квадрат. ф-лу .

Обладает 4 свойствами:

1. положит. определена, т.е.

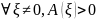
2. отрицат. определена, т.е.

3. неположит. (неотрицат.) определена, т.е.

4. не является знакоопределеляющей квадр. ф-лой, если

Составим матрицу этой кв. ф-ции

Критерий Сильвестра: для того, чтобы

1. была положит. определена необ. и дост. чтобы

2. отрицательно определена необ. и дост. чтобы

3. была заведомо нестрого опр. (для неотрицат) и

(для неположит.) кв. формул.

4. во всех ост. случаях квадратичн. форма не явл. знакоопределяющей.

ТЕОР: Пусть ф-ция f(M) определена, непрерывна и имеет непрерыв. частн. произв. 2-ого порядка в нек. окрестности т.M^o и её частн. произв. 1-ого порядка = 0. Если 2-ой диф-л

1. Является положит. опред. квадратичн.ф-мой то в т.M^o будет локальным min ф-ции

2. Является отриц. определ. кв. формой, то в т. M^o – локальный max

3. Если явл. нестрого опред. кв. ф-мой, то в т. M^o экстремум можеть ыбыть, а можети не быть.

4. Если не явл. знакоопред. кв. формой, то в т. M^o экстремума нет.