Вопрос 1 Опр. Инт-л Римана

Пусть дан . Разбиением T отрезка называется набор точек или набор отрезков , где . Будем обозначать .

П усть на отрезке задана функция . Возьмём некоторое разбиение отрезка и в каждом отрезке выберем точку . Сумма 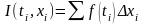называется интегральной. Число I называется интегралом от , если для для всех разбиений T с при любом выборе точек будет (т.е. ). Обозначается ­ (интеграл, определённый таким образом, называется интегралом Римана). Если не ограничена на , то неинтегрируема на .

Вопрос 2 Основные определения

1. Неопределённый интеграл: Пусть ∆ - конечный или бесконеч. отрезок числ. оси, т.е. интервал, полуинтервал, или отрезок. На отрезке ∆ задана f(x) и F(x).

ОПР: Фун-я F(x) наз. первообразной ф-ции f(x) на ∆, если F’(x) дифф-ма на ∆ и F’(x)= f(x) для всех

ОПР: Пусть f(x) определена на ∆. Совокупность всех ёё первообр. на ∆ наз-ся неопр. интегралом и обозн.

2. Определённый нтервал: см. Вопрос 1 (инт-л Римана=опр. инт-л)

Вопрос 3-5 Необх и дост усл интегрируемости. Верхн и нижн суммы Дарбу. Св-ва

Изначально считаем, что на ограничена и пусть задано разбиение Т отрезка на отр. , где . На каждом из отрезков найдём M_i – точная верхняя грань и m_i – точная нижн. грань ф-ции при х ε

S= и s=m_i - соответственно верхняя и нижняя суммы Дарбу при разбиении T.

С войства:

1. Любая интегр. ∑ заключена между верх. и нижн. ∑ Дарбу отвечающие данному разбиению Т.

2. Если к уже имеющ. точкам разбиения добавить ещё одну точку, то нижн. ∑ Дарбу может лишь возрасти, а верхняя – лишь уменьшиться.

3. Любая нижн. ∑ Дарбу не превосходит ∀ верх. ∑ Дарбу, если даже они отвечают различ. разбиениям .

4. Множество всех нижн. ∑ Дарбу есть огран. сверху, напр. ∀ верхн. ∑, значит у этого мн-ва есть точная верхняя грань Множество всех верхн. ∑ Дарбу есть огран. снизу, напр. ∀ нижн. ∑, значит у этого мн-ва есть точная нижняя грань ТЕОР: Для существования опр. инт-ла необ. и дост, чтобы 1. Предел

2. Чтобы для ∀ ε > 0: как только ∆< ẟ, то

Вопрос 6 Классы интегрируемых функций

1. Если непрерывна на , то интегрируема на .

Док-во: Если f(x) непрерывна на , то согласно теор. Кантора она равномерно непрерывна на этом отрезке. Это означает, что для для любых и выполн. нер-во

Возьмём число и выберем по нему такое разбиение отрезка чтобы . Отсюда следует, что

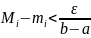
2. Если монотонна и ограничена на , то интегрируема на .

3. ОПР: Ф-ция наз. кусочно-непрерывной на , если она имеет на этом отрезке конечн. число точек разрыва 1 рода, а в ост. точка она непрерывна.

ТЕОР: кусочно-непрерывная на ф-ция интегрируема на этом отрезке.

Вопрос 7 Св-ва интегрируемых ф-ций

1. Если и интегрируемы на , то .

2. Если интегрируема на и , то интегрируема на ­ и .

3. Если и интегрируемы на , то * так же интегрируема на

4. Если интегрируема на и ≥d>0, , то интегрируема на

5. Если интегрируема на , то она интегрируема на ∀ отрезке : .

6. Если a<c<b и ф-ция интегрируема на , то она интегрируема на и (и наоборот) и справедлива ф-ла

7. Если 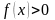и интегрируема на , то

8. Если интегрируема на , то интегрируем на и

9. Если интегрируема на , то она интегрируема на и

10. Если и интегрируемы на и ≥ , , то

11. Пусть и интегрируема на , то . Если , то

Вопрос 8 Теорема о среднем значении

Пусть и интегрируемы на , сохраняет знак на и . Тогда и . Если, кроме того, непрерывна на , то найдутся такие точки что f(x₁) = m, f(x₂) = M и число ή: f(ή) - µ и .

Вопрос 9 Теорема о дифференцировании по верх. пределу

Если интегрируема на и в т. x₀ , то ф-ция F(x)= диффер в т. x₀ и ( )

Замечание: Если х₀=а , то речь идёт о правой производной, если х₀≠а, то речь идёт о левой производной.

Док-во: . Равенство (согласно т. о средн. значении) можно записать при

Замечание: Если непрерывна на , то для всех , а это значит, что F(x) – первообр f(x) на .

Вопрос 10 теорема Ньютона-Лейбница

Формула Ньютона-Лейбница: Если непрерывна на и – какая-то первообразная для на , то .

Док-во: Из следствий Теоремы о дифференцировании по верх. пределу следует, что так как f(x) непрерывна на , то ф-ция является одной из её первообр на . Т.к. все первообр. отличаются на const, то . Положим в этом соотнш. x=a. Получим: . Тогда Положим x=b:

Вопрос 11 Формула замены переменной и интегрирования по частям

Пусть U(x) и V(x) – непрерывны вместе со своими производными на , то

Док-во:

Если ф-ция f(x) непрерывна на ∆х, а ф-ция φ(t) непрерывна вместо со своей производной на ∆ t, то , где и φ(α)=а, φ(β)=b

Док-во: Пусть F(x) – какая-либо первообр f(x), тогда – первообр ф-ции , т.к.

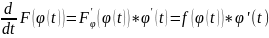
По ф-ле Ньютона-Лейбница будем иметь

Вопрос 12 Геометрические и физические приложения опр. инт-ла

1.1 Вычисление площади плоской фигуры

 Пусть функция   непрерывна и неотрицательна на отрезке [a, b]. Тогда площадь фигуры, ограниченной осью ОХ, отрезками прямых x = a, x = b и графиком функции  , может быть вычислена по формуле Если   на отрезке [a, b],   - непрерывные функции, то площадь фигуры, ограниченной прямыми х = а, x = b, графиками функций   вычисляется по формуле 

1.2. Вычисление площади криволинейного сектора. 

Пусть кривая AB задана в полярных координатах уравнением  ,  , причем   - непрерывная и неотрицательная на отрезке   функция. Фигуру, ограниченную кривой AB и двумя полярными радиусами, составляющими с полярной осью углы  , будем называть криволинейным сектором.

Площадь криволинейного сектора может быть вычислена по формуле    

1.3 Вычисление площади плоской фигуры, если граница задана параметрически

Кривая замкнута α<t<β . Граница обходится в положит. напр при t от α до β => область остается слева.

2. Вычисление длины дуги плоской кривой

2.1 Если функция y = f(x) непрерывна вместе с её производной f'(x) на отрезке [a, b], то длина дуги AB, где A(a,f(a)), B(b, f(b)), выражается формулой .                                       

2.2. Если кривая задана параметрическими уравнениями    , где x(t), y(t) - дифференцируемые функции, то длина дуги    .          

2.3. Если дуга задана в полярных координатах  ,   , то длина дуги

    .    

3. Вычисление объемов. 

3.1. Вычисление объема тела по известным площадям параллельных сечений.

Если известны площади сечений тела плоскостями, перпендикулярными оси OX, т. е., зная х, мы можем вычислить площадь сечения S = S (x). Тогда объем тела   в предположении, что S(x) - интегрируемая функция.

3.2. Вычисление объема тела вращения:

а) Кривая трапеция до Ох вращается вокруг Ох: если тело образовано вращением криволинейной трапеции, ограниченной кривой y = f(x), осью OX и двумя прямыми x = a и x = b(a < b) вокруг оси OX, то объем тела  ;

б) Кривая трапеция до Оу вращается вокруг Оу: если тело образовано вращением фигуры, ограниченной кривой  , прямыми y=c, y=d (c<d) и осью OY, вокруг оси OY, то его объем  ;

в) Трапеция до Ох вращается вокруг Оу: если тело образовано вращением вокруг оси OY фигуры, ограниченной линией y = f (x), прямыми x = a, x = b   и осью OX, то его объем можно вычислить по формуле  ;

г) если вращается вокруг полярной оси криволинейный сектор, ограниченный дугой  , двумя полярными радиусами   и  , то  объем полученного тела может быть вычислен по формуле  .

4. Вычисление площади поверхности вращения

4.1. Поверхность, образованная вращением кривой  , a < x < b вокруг оси OX, имеет площадь   .

4.2. Если кривая задана параметрическими уравнениями     , причем  , то .

 4.3. Если дуга  ,  , задана в полярной системе координат кривой, и вращается вокруг полярной оси, то площадь поверхности вращения можно вычислить по формуле

5.Вычисление статических моментов

Пусть на плоскости Оху задана система материальных точек M₁ (x₁; y₁), М₂(х₂; у₂),..., Мn(хn; уn) соответственно с массами m₁, m₂,... ...,m_n.

Статическим моментом S_x системы материальных точек относительно оси Ох называется сумма произведений масс этих точек на их ординаты (т. е. на расстояния этих точек от оси Ох):

Аналогично определяется статический момент Sy этой системы относительно оси Oy: 

Если массы распределены непрерывным образом вдоль некоторой кривой, то для выражения статического момента понадобится интегрирование.

6. Вычисление моментов инерции

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении: где:

dm = ρ dV — масса малого элемента объёма тела dV,

ρ — плотность,

r — расстояние от элемента dV до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то