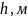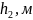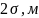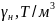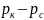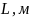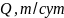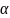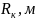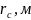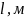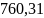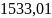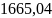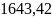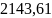Глава 2 - установившийся приток реального газа к горизонтальной скважине по линейному и нелинейному законам фильтрации

2.1 Дебит газа горизонтальной скважины

В соответствии с аналогией фильтрации несжимаемой жидкости и реального газа известные решения для фильтрации несжимаемой жидкости легко преобразуются для фильтрации газа. Для этого необходимо объемный расход заменить весовым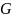 , а отношение 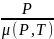  - обобщенной функцией Лейбензона[4]:

С учетом уравнения газового состояния:

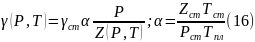
функция (1.1) принимает следующий вид:

где P -давление;

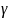 - удельный вес газа;

  - коэффициент абсолютной вязкости;

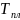  - пластовая температура газа;

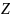  - коэффициент сверхсжимаемости   газа;

ст  - символ, означающий стандартные условия.

Интеграл (1.3) рассчитывается численным способом. Усредняя параметры 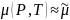  и 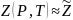  и применяя их к функции (1.3) для преобразования, например, формулы притока нефти к горизонталь­ной скважине, получаем формулу дебита горизонтальной газовой скважи­ны[4]:

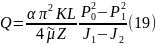
2.2 Установившийся приток реального газа к горизонтальной скважине по нелинейному закону фильтрации

Задача решается по двухзонной схеме притока к горизонтальной скважине, дренирующей полосообразный однородно-анизотропный пласт с двухсторонним симметричным контуром питания (рис. 1.1). Получено следующее уравнение притока[4]:

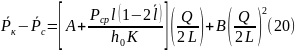
Где:

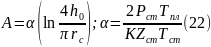
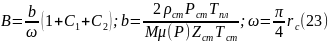
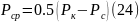
Усредняя параметры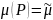   и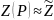   , интегрируя формулу (21) в пределах от   до 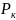 , получаем выражение для левой части уравнения при­тока (20):

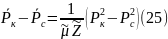
Здесь 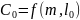 - добавочные фильтрационные сопротивления, обуслов­ленные перфорацией колонны, (рисунок 3);

 

Рисунок 3 - Модель горизонтальной скважины

 

   - добавочные фильтрационные сопротивления, обуслов­ленные относительным расположением горизонтального ствола;

    - добавочные фильтрационные сопротивления, обуслов­ленные нелинейным законом фильтрации.

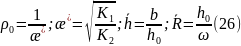
Где:

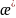- коэффициент анизотропии пласта;

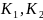 -коэффициенты проницаемости по горизонтали и вертикали

соответственно;

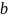 -расстояние от кровли пласта до положения горизонтального ствола;

  - горизонтальная толщина продуктивного пласта.

 

Глава 3 - расчетная часть

Задача 1.

Проведем расчёт притока жидкости (дебита) единицы длины горизонтальной скважины по формуле:

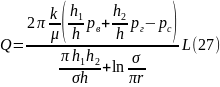
Таблица 1.1. Исходные данные

22	14	0,106	2,4	300	0,908	1,2

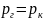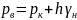Полагая, что - р и , получаем следующие значения дебитов для различных длин горизонтальных скважин:

Таблица 1.2. Полученные результаты.

	1	2,4	13,7	20	50	100
	2,91	7,00	40	58,2	145,5	291

Учитывая то положение, что при расчетах для определения дебита горизонтальной скважины конечной длины использовалась формула для бесконечной горизонтальной скважины, полученные результаты следует считать ориентировочными, а формула (16) может быть использована для оценочных расчетов.

Задача 2.

Рассчитаем приток жидкости (дебита) к многоствольной горизонтальной скважине по уравнению Борисова Ю.П., Пилатовского В.П., Табакова В.П.:

Таблица 2.1. Исходные данные.

,МПА	,МПа
23,1	16	8	90	330	0,1	300

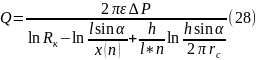
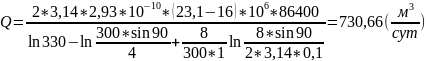
Рассчитываем приток жидкости к многоствольной горизонтальной скважине по уравнению Григулецкого В.Г., Никитина Б.А.:

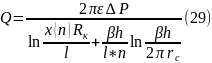
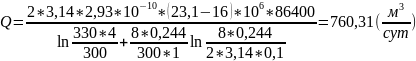
Рассчитываем приток жидкости по формуле для одноярусной многоствольной горизонтальной скважине:

Таблица 2.2. Полученные результаты.

Борисов	Григулецкий	Одноярусная	n
			1
			2
			3
			4