2.2 Математическая модель нестационарного теплопереноса для двухслойной системы

Применение в методах неразрушающего контроля теплофизических свойств материалов теплового воздействия постоянной мощности от круглого плоского нагревателя в виде диска, встроенного в подложку измерительного зонда, достаточно обосновано и полно представлено в работах [5, 6, 9].

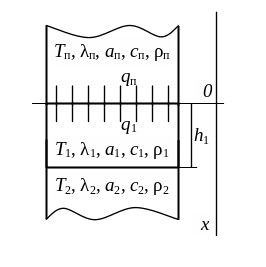
С целью повышения точности определения теплофизических свойств при неразрушающем контроле двухслойных материалов в данной работе рассматривается система, состоящая из ограниченного и двух полуограниченных тел (рисунок 2.3).

Для решения задач, связанных с нахождением температурного поля, необходимо иметь дифференциальное уравнение теплопроводности. Под дифференциальным уравнением обычно понимают математическую зависимость, выражаемую дифференциальным уравнением между физическими величинами, характеризующими изучаемое явление, причем эти физические величины являются функциями пространства и времени. Такое уравнение характеризует протекание физического явления в любой точке тела в любой момент времени [3].

Дифференциальное уравнение теплопроводности дает зависимость между температурой, временем и координатами элементарного объема [3].

Теоретическое обоснование теплового метода неразрушающего контроля двухслойных изделий, сформулированное в работе [21], распространяется на полуограниченные тела и не учитывает оттоки тепла в материал подложки измерительного зонда. Полученное в работе [21] решение краевой задачи теплопроводности не позволяет с достаточной точностью определять теплофизические свойства слоев двухслойных объектов.

Рисунок 2.3 – Тепловая схема метода при воздействии плоского бесконечного источника тепла на двухслойное изделие.

Ограниченный стержень толщиной h₁ приведен в соприкосновение с двумя полуограниченными стержнями. Теплофизические свойства стержней различны. В начальный момент времени на свободном конце ограниченного стержня начинает действовать источник тепла постоянной мощности q, который действует на протяжении всего процесса нагрева.

Требуется найти распределение температуры по длине стержней в любой момент времени. Можно сформулировать краевую задачу теплопроводности следующим образом:

	(2.1)
	(2.2)
	(2.3)
	(2.4)
	(2.5)
	(2.6)
	(2.7)
	(2.8)
	(2.9)

_{Дифференциальное уравнение теплопроводности устанавливает связь между временными и пространственными изменениями температуры тела; оно математически описывает перенос тепла внутри тела. Для того чтобы найти температурное поле внутри тела в любой момент времени, т. е. чтобы решить дифференциальное уравнение, надо знать распределение температуры внутри тела в начальный момент времени (начальное условие), геометрическую форму тела и закон взаимодействия между окружающей средой и поверхностью тела (граничное условие) [3].}

_{Совокупность начального и граничного условий называется краевыми условиями; начальное условие называется временным}

_{краевым условием, а граничное условие ─ пространственным краевым условием [3, стр.24]}

Систему уравнений (2.1) – (2.9) можно решить методом интегрального преобразования Лапласа.

Для неразрушающего теплофизического контроля свойств двухслойных систем интерес представляют изменения температуры и плотности теплового потока от времени на поверхности первого тела (плоскость с координатой x = 0).

Очевидно, что для определения теплофизических свойств слоев двухслойной системы необходимо «прогреть» ее на глубину больше h₁, поэтому необходимо получить решение краевой задачи относительно q при больших значениях времени τ.

Решение краевой задачи теплопроводности (2.1) – (2.9) имеет вид:

(2.10)

Данное решение возможно использовать для нахождения ТФС первого тела, если известна толщина h₁ и ТФС подложки зонда (ε_п) или для нахождения толщины первого тела при известных ТФС.

Граничные условия краевых задач теплопроводности

Граничные условия могут быть заданы в виде граничных условий первого, второго, третьего или четвертого рода.

Граничные условия первого рода обычно задают в виде известного закона изменения во времени температуры на поверхности исследуемого образца. Для тела, представленного на рис 1.3, а граничные условия первого рода (ГУ-1) имеют вид:

T(0, τ) = ϕ₁ (τ);

T(H, τ) = ϕ₂ (τ).

Функции ϕ₁(τ), ϕ₂(τ) могут иметь вид:

T (0, τ) = ϕ₁ (τ) = T₀(1 − e^{− 2τ});

T(H, τ) = ϕ₂ (τ) = kτ.

В общем случае граничные условия имеют вид

T(x_п , y_п , z_п ,τ) = ϕ₁(x_п , y_п , z_п ,τ) ,

где x_п , y_п , z_п − координаты точек поверхности тела. [1, стр.11]

Граничные условия второго рода обычно задают в виде известных функций изменения во времени теплового потока на поверхности тела. С учетом закона Фурье

q_x= для случая геометрии образца, представленного на рис. 1.3, а, получаем запись граничных условий второго рода (ГУ-2) в виде