МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(ФГБОУ ВПО «ВГТУ»)

Институт машиностроения и аэрокосмической техники

Кафедра оборудования и технологии сварочного производства

КУРСОВОЙ ПРОЕКТ

по дисциплине «Расчет и проектирование сварных соединений»

Тема «Расчет и проектирование сварной подкрановой балки и сварной колонны»

Вариант 18

Выполнил: студент СП – 141 С.С. Толокнёв

^{Группа Подпись, дата инициалы, фамилия}

Руководитель: И. Б. Корчагин

^{Подпись, дата инициалы, фамилия}

Нормоконтролёр: И. Б. Корчагин

^{Подпись, дата инициалы, фамилия}

Защищена Оценка

^Дата

Воронеж 2017

Замечания руководителя

Содержание

Замечания руководителя			2
Задание на курсовой проект			4
Введение			5
1	Расчет и проектирование сварной подкрановой балки		6
	1.1	Данные для расчета	6
	1.2	Построение эпюр M и Q в характерных сечениях балки	7
	1.3	Определение высоты балки	16
	1.4	Конструирование сечения балки	18
	1.5	Проверка прочности сечения балки	20
	1.6	Проверка общей устойчивости балки	26
	1.7	Проверка устойчивости элементов балки	28
	1.8	Конструирование и расчет сварных соединений балки	34
	1.9	Конструирование и расчет опорных плит балок	39
2	Расчет и проектирование сварной колонны		41
	2.1	Данные для расчетов	41
	2.2	Расчет и конструирование сечения колонны, проверка прочности колонны	42
	2.3	Проверка устойчивости колонны	46
	2.4	Конструирование и расчет раскосой решетки	49
	2.5	Конструирование и расчет диафрагм	51
	2.6	Конструирование и расчет оголовка колонны	52
	2.7	Конструирование и расчет базы колонны	54
	2.8	Конструирование и расчет сварных соединений колонны	56
Заключение			59
Список литературы			60
Приложение А Балка подкрановая			61
Приложение Б Колонна			63

ЗАДАНИЕ

на курсовой проект

По дисциплине «Расчет и проектирование сварных соединений»

Тема работы «Расчет и проектирование сварной подкрановой балки и сварной колонны»

Студент группы СП-141 Толокнёв Сергей Сергеевич

№ варианта 18

Данные для расчета:

1. Подкрановая балка: L = 18 м, Р = 4 Т, q = 1 Т/м, d = 2 м.

2. Колонна: N₁ = 15 T, N₂ = 16 Т, L = 23 м, e = 1,5 м.

Введение

Развитие современного машиностроения, судостроения, авиастроения и строительства невозможно представить без сварочного производства. Развитие сварки коренным образом изменило структуру изготовления металлоконструкций в этих отраслях. В общем объеме их выпуска процент сварных конструкций неуклонно растет. Такие конструкции должны соответствовать требованиям высокой эксплуатационной надежности, быть высокотехнологичными и экономичными. Применение сварки при их изготовлении позволяет наиболее эффективно использовать прокатные, гнутые, штампованные, кованные и литые заготовки. При решении множества технических задач сварное исполнение конструкции является единственно возможным.

За время, прошедшее с начала широкого применения сварки в металлических конструкциях, накопилось много опытных и теоретических исследований, посвященных работоспособности и принципам оценки прочности основных типов сварных швов и соединений. На основе этих исследований установлены соответствующие расчетные методики, правила и нормы проектирования сварных соединений и конструкций, гарантирующие надежную работу их в течение всего срока службы.

Конкретной задачей данного курсового проекта является обучение выбору расчетной схемы конструкции, материалов, наиболее полно удовлетворяющих требованиям эксплуатации и технологичности изготовления конструкции, методике наиболее рационального, технически грамотного и экономичного изготовления отдельных узлов конструкции, методике расчета на прочность сварных соединений конструкции, умению пользоваться технической литературой, нормативными документами и другими справочными материалами.

1 Расчет и проектирование сварной подкрановой балки

Расчет и проектирование сварной подкрановой балки состоит из следующих этапов:

1. определение расчетной схемы с указанием действующих нагрузок;

2. построение эпюр изгибающих моментов М и перерезывающих сил Q в характерных сечениях балки;

3. выбор материала балки;

4. определение высоты балки h и выбор типа сечения;

5. конструирование сечения балки;

6. проверка прочности сечения балки;

7. проверка общей устойчивости балки;

8. проверка местной устойчивости элементов балки;

9. конструирование и расчет сварных соединений балки;

10. конструирование и расчет опорных плит балки;

11. разработка графической части проекта сварной балки.

1.1 Данные для расчетов

Исходными данными для расчета являются расчетная схема балки с заданными нагрузками, длина балки, норма жесткости f_max, а также минимальная температура эксплуатации. Расчетная схема сварной подкрановой балки приведена на рисунке 1.1.

Рисунок 1.1 – Расчетная схема подкрановой балки

Исходные данные: L = 18 м, Р = 4 Т, q = 1 Т/м, d = 2 м.

Для подкрановых балок норму жесткости назначают как

Тогда, для заданной балки имеем

см = 3,6 см.

1.2 Построение эпюр M и Q в характерных сечениях балки

Используя принцип независимости действия сил, найдем M_q и Q_q от действия распределенных сил и M_p и Q_p от действия перемещающейся по балке спаренной нагрузки, при ее расположении в сечениях x = 0; x = 0,1L; x = 0,2L; x = 0,3L; x = 0,4L; x = 0,5L. Спаренная нагрузка может перемещаться от одного конца балки к другому.

1. Построение эпюр M_q и Q_q от действия распределенных сил с шагом 0,1L:

где z – расстояние до рассматриваемого сечения балки.

Рассчитанные значения M_q и Q_q сведены в таблицу 1.1.

Таблица 1.1

z	Mq, кг·м	Qq, кг
0	0	9 000
0,1L	14 580	7 200
0,2L	25 920	5 400
0,3L	34 020	3 600
0,4L	38 880	1 800
0,5L	40 500	0

Расчетная схема и эпюры M_q и Q_q приведены на рисунке 1.2.

Рисунок 1.2 - Эпюры M_q и Q_q от действия распределенной силы q

2. Построение эпюр M_p и Q_p от действия перемещающейся по балке спаренной нагрузки:

1. При x = 0

;

кг;

кг.

Разобьем балку на участки:

Первый участок: 0 ≤ z₁ ≤ d

M_P = R_A · z₁ – P · z₁;

При z₁ = 0: M_P = 0 кг·м; Q_P = R_A =7556 кг;

При z₁ = d: M_P = R_A · d – P · d = 7556 · 2 – 4000 · 2 = 7112 кг·м;

Q_P = R_A – P = 7556 – 4000 = 3556 кг.

Второй участок 0 ≤ z₂ ≤ L – d

M_P = R_A · (d + z₂) – P · (d + z₂)  P · z₂;

При z₂ = 0: M_P = R_A · d – P · d = 7112 кг·м;

При z₂ = L – d: M_P = R_A · (d + (L – d)) – P · (d + (L – d))  P · (L – d) = 0 кг·м;

Q_P = R_A – 2 · P = 7556 – 2 · 4000 = 444 кг.

Расчетная схема балки и эпюры M_Р и Q_Р для данного положения спаренной нагрузки приведены на рисунке 1.3.

Рисунок 1.3 – Расчетная схема балки и эпюры M_Р и Q_Р при положении спаренной нагрузки в сечении х = 0.

2. При x = 0,1L

R_A – 2 · P + R_B = 0;

R_B · L  Р · (0,1 · L – 0,5 · d) – P · (0,1 · L + 0,5 · d) = 0;

кг;

R_A = 2 · P  R_B = 2 · 4000 – 800 = 7200 кг.

Разобьем балку на участки:

Первый участок 0 ≤ z₁ ≤ (0,1 · L - 0,5 · d)

M_P = R_A · z₁;

При z₁ = 0: M_P = 0 кг·м;

При z₁ = (0,1 · L - 0,5 · d): M_P = 7200 · (0,1 · 18 - 0,5 · 2) = 5760 кг·м;

Q_P = R_A = 7200 кг.

Второй участок 0 ≤ z₂ ≤ d

M_P = R_A · ((0,1 · L - 0,5 · d) + z₂)  P · z₂;

При z₂ = 0: M_P = 5760 кг·м;

При z₂ = d: M_P = 7200 · ((0,1 · 18 - 0,5 · 2) + 2)  4000 · 2 = 12160 кг·м;

Q_P = R_A – P = 7200 – 4000 = 3200 кг.

Третий участок 0 ≤ z₃ ≤ L – (0,1 · L + 0,5 · d)

M_P = R_B · z₃;

При z₃ = L – (0,1 · L + 0,5 · d): M_P = 12160 кг·м;

При z₃ = 0: M_P = 0 кг·м;

Q_P = R_B = 800 кг.

Расчетная схема балки и эпюры M_Р и Q_Р для данного положения спаренной нагрузки приведены на рисунке 1.4.

Рисунок 1.4 – Расчетная схема балки и эпюры M_Р и Q_Р при положении спаренной нагрузки в сечении х = 0,1L

3. При x = 0,2L

R_A – 2 · P + R_B = 0;

R_B · L  Р · (0,2 · L – 0,5 · d) – P · (0,2 · L + 0,5 · d) = 0;

кг;

R_A = 2 · P  R_B = 2 · 4000 – 1600 = 6400 кг.

Разобьем балку на участки:

Первый участок 0 ≤ z₁ ≤ (0,2 · L – 0,5 · d)

M_P = R_A · z₁;

При z₁ = 0: M_P = 0 кг·м;

При z₁ = (0,2 · L – 0,5 · d): M_P = 6400 · (0,2 · 18 – 0,5 · 2) = 16640 кг·м;

Q_P = R_A = 6400 кг.

Второй участок 0 ≤ z₂ ≤ d

M_P = R_A · ((0,2 · L – 0,5 · d) + z₂)  P · z₂;

При z₂ = 0: M_P = 16640 кг·м;

При z₂ = d: M_P = 6400 · ((0,2 · 18 – 0,5 · 2) + 2)  4000 · 2 = 21440 кг·м;

Q_P = R_A – P = 6400 – 4000 = 2400 кг.

Третий участок 0 ≤ z₃ ≤ L – (0,2 · L + 0,5 · d)

M_P = R_B · z₃;

При z₃ = L – (0,2 · L + 0,5 · d): M_P = 21440 кг·м;

При z₃ = 0: M_P = 0 кг·м;

Q_P = R_B = 1600 кг.

Расчетная схема балки и эпюры M_Р и Q_Р для данного положения спаренной нагрузки приведены на рисунке 1.5.

Рисунок 1.5 – Расчетная схема балки и эпюры M_Р и Q_Р при положении спаренной нагрузки в сечении х = 0,2L

4. При x = 0,3L

R_A – 2 · P + R_B = 0;

R_B · L  Р · (0,3 · L – 0,5 · d) – P · (0,3 · L + 0,5 · d) = 0;

кг;

R_A = 2 · P  R_B = 2 · 4000 – 2400 = 5600 кг.

Разобьем балку на участки:

Первый участок 0 ≤ z₁ ≤ (0,3 · L – 0,5 · d)

M_P = R_A · z₁;

При z₁ = 0: M_P = 0 кг·м;

При z₁ = (0,3 · L – 0,5 · d): M_P = 5600 · (0,3 · 18 – 0,5 · 2) = 24640 кг·м;

Q_P = R_A = 5600 кг.

Второй участок 0 ≤ z₂ ≤ d

M_P = R_A · ((0,3 · L – 0,5 · d) + z₂)  P · z₂;

При z₂ = 0: M_P = 24640 кг·м;

При z₂ = d: M_P = 5600 · ((0,3 · 18 – 0,5 · 2) + 2)  4000 · 2 = 27840 кг·м;

Q_P = R_A – P = 5600 – 4000 = 1600 кг.

Третий участок 0 ≤ z₃ ≤ L – (0,3 · L + 0,5 · d)

M_P = R_B · z₃;

При z₃ = L – (0,3 · L + 0,5 · d): M_P = 2400 · (18 – (0,3 · 18 + 0,5 · 2)) =27840 кг·м;

При z₃ = 0: M_P = 0 кг·м;

Q_P = R_B = 2400 кг.

Расчетная схема балки и эпюры M_Р и Q_Р для данного положения спаренной нагрузки приведены на рисунке 1.6.

Рисунок 1.6 – Расчетная схема балки и эпюры M_Р и Q_Р при положении спаренной нагрузки в сечении х = 0,3L

5. При x = 0,4L

R_A – 2 · P + R_B = 0;

R_B · L  Р · (0,4 · L – 0,5 · d) – P · (0,4 · L + 0,5 · d) = 0;

кг;

R_A = 2 · P  R_B = 2 · 4000 – 3200 = 4800 кг.

Разобьем балку на участки:

Первый участок 0 ≤ z₁ ≤ (0,4 · L – 0,5 · d)

M_P = R_A · z₁;

При z₁ = 0: M_P = 0 кг·м;

При z₁ = (0,4 · L – 0,5 · d): M_P = 4800 · (0,4 · 18 – 0,5 · 2) = 29760 кг·м;

Q_P = R_A = 4800 кг.

Второй участок 0 ≤ z₂ ≤ d

M_P = R_A · ((0,4 · L – 0,5 · d) + z₂)  P · z₂;

При z₂ = 0: M_P = 29760 кг·м;

При z₂ = d: M_P = 4800 · ((0,4 · 18 – 0,5 · 2) + 2)  4000 · 2 = 31360 кг·м;

Q_P = R_A – P = 4800 – 4000 = 800 кг.

Третий участок 0 ≤ z₃ ≤ L – (0,4 · L + 0,5 · d)

M_P = R_B · z₃;

При z₃ = L – (0,4 · L + 0,5 · d): M_P = 2400 · (18 – (0,4 · 18 + 0,5 · 2)) =31360 кг·м;

При z₃ = 0: M_P = 0 кг·м;

Q_P = R_B = 3200 кг.

Расчетная схема балки и эпюры M_Р и Q_Р для данного положения спаренной нагрузки приведены на рисунке 1.7.

Рисунок 1.7 – Расчетная схема балки и эпюры M_Р и Q_Р при положении спаренной нагрузки в сечении х = 0,4L

6. При x = 0,5L

R_A – 2 · P + R_B = 0;

R_B · L  Р · (0,5 · L – 0,5 · d) – P · (0,5 · L + 0,5 · d) = 0;

кг;

R_A = 2 · P  R_B = 2 · 4000 – 4000 = 4000 кг.

Разобьем балку на участки:

Первый участок 0 ≤ z₁ ≤ (0,5 · L – 0,5 · d)

M_P = R_A · z₁;

При z₁ = 0: M_P = 0 кг·м;

При z₁ = (0,5 · L – 0,5 · d): M_P = 4000 · (0,5 · 18 – 0,5 · 2) = 32000 кг·м;

Q_P = R_A = 4000 кг.

Второй участок 0 ≤ z₂ ≤ d

M_P = R_A · ((0,5 · L – 0,5 · d) + z₂)  P · z₂;

При z₂ = 0: M_P = 32000 кг·м;

При z₂ = d: M_P = 4000 · ((0,5 · 18 – 0,5 · 2) + 2)  4000 · 2 = 32000 кг·м;

Q_P = R_A – P = 4000 – 4000 = 0 кг.

Третий участок 0 ≤ z₃ ≤ (0,5 · L – 0,5 · d)

M_P = R_B · z₃;

При z₃ = (0,5 · L – 0,5 · d): M_P = 4000 · (0,5 · 18 – 0,5 · 2) = 32000 кг·м;

При z₃ = 0: M_P = 0 кг·м;

Q_P = R_B = 4000 кг.

Расчетная схема балки и эпюры M_Р и Q_Р для данного положения спаренной нагрузки приведены на рисунке 1.8.

Рисунок 1.8 – Расчетная схема балки и эпюры M_Р и Q_Р при положении спаренной нагрузки в сечении х = 0,5L

1.3 Определение высоты балки

Для заданной подкрановой балки выбираем материал – сталь класса С38/23. Механические характеристики и расчетные сопротивления данной стали приведены в таблице 1.2:

Таблица 1.2

Механические свойства при растяжении			Расчетное сопротивление, кг/см2
Временное сопротивление в, кг/см2	Предел текучести т, кг/см2	Относительное удлинение , %	Сжатие, растяжение, изгиб, R	Срез, Rср	Смятие торцевой поверхности при наличии пригонки, Rсм
3 800	2 300	25	2 100	1 300	3 200

Высота балки определяется исходя из условия жесткости и условия наименьшего веса (условия прочности).

Высоту балки из условия жесткости определяют по формуле:

где R = 2100 – расчетное сопротивление материала балки;

m₁ = 0,9 – коэффициент условий работы балки;

n₁ = 1,1 – коэффициент перегрузки для распределенной нагрузки;

n₂ = 1,3 – коэффициент перегрузки для сосредоточенной нагрузки;

Е = 2 · 10⁶ – модуль упругости материала балки.

Расчет ведут, принимая размерность линейных величин в см, расчетных сопротивлений и напряжений – в кг/см², изгибающих моментов – в кг·см.

Для заданной балки:

см ≈ 313 см.

Высота балки из условия наименьшего веса (условия прочности) определяется по формуле:

где = максимальное значение момента от спаренной нагрузки;

М_q^* - максимальное значение момента от распределенной нагрузки в сечении, где действует ;

s_в – толщина вертикального листа, условно принимаем равной 1 см.

Для заданной балки

см.

1.4 Конструирование сечения балки

Высота балки и размеры других конструктивных элементов подбираются методом последовательных приближений с использованием эмпирических зависимостей.

При конструировании необходимо учитывать, что сечение балки должно удовлетворять как условию жесткости, так и условию прочности.

Первоначально назначают некоторое промежуточное значение высоты h между значениями высот h_ж и h_э.

Принимаем высоту пролета балки h = 125 см.

Толщина вертикального листа определяется по эмпирической формуле:

Тогда:

≈ 0,9 см.

Толщина горизонтальных листов s_г обычно больше толщины вертикальных листов и принимается равной:

s_г = (1,0…1,2) · s_в.

Для рассматриваемой балки примем s_г = 1,2 · s_в = 1,2 · 0,9 = 1,07 см.

Ширину горизонтальных листов примем b_г = 20 · s_г = 21,34 см.

Высота вертикального листа h_в = h – 2 · s_г = 125 – 2 · 1,07 = 122,86 см.

Поперечное сечение балки представлено на рисунке 1.9.

Рисунок 1.9 – Поперечное сечение балки

1.5 Проверка прочности сечения балки

По принятым размерам балки определяем фактический момент инерции ее сечения:

Тогда:

см⁴.

Максимальные нормальные напряжения в сечении, где действует максимальный изгибающий момент от спаренной силы, определятся по формуле:

Для заданной балки имеем

кг/см²  R = 2100 кг/см².

Условие прочности выполняется. При этом, значение _max отличается от величины расчетного сопротивления R не более чем на ±5 %, что допустимо.

Максимальные касательные напряжения в сечении, где действует максимальная перерезывающая сила от спаренной сосредоточенной нагрузки, определяется по формуле:

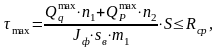
где S – статический момент половины сечения балки относительно оси x;

R_ср – расчетное сопротивление на срез (таблица 1.2).

Статический момент фигуры определяется как произведение ее площади на расстояние от центра тяжести фигуры до рассматриваемой оси. Статический момент сложной фигуры определяется как сумма статических моментов элементарных фигур, на которые ее можно разбить.

Статический момент половины сечения балки относительно оси x определим как сумму статических моментов горизонтального листа S₁ и половины вертикального листа S₂:

= 3092,98 см³.

Тогда:

= 186.4 кг/см²  R_ср = 1300 кг/см².

Проверим эквивалентные напряжения в сечениях x = 0; x = 0,1L; x = 0,2L; x = 0,3L; x = 0,4L; x = 0,5L от перемещающейся по балке спаренной нагрузки по формуле:

Нормальные напряжения _ж определяются по формуле:

где  максимальное значение изгибающего момента от спаренной нагрузки;

 значение изгибающего момента от распределенной нагрузки в сечении, где действует .

Касательные напряжения определяются как:

где - максимальное значение перерезывающей силы от спаренной нагрузки;

- значение перерезывающей силы от распределенной нагрузки, где действует .

Значения напряжений в соответствующих сечениях сведены в таблицу 1.3:

Таблица 1.3

х, м	ж, кг/см2	ж, кг/см2	экв, кг/см2
0	0	198,18	343,26
0,1L	604,23	121,39	639,77
0,2L	1162,45	91,04	1173,1
0,3L	1561,17	60,69	1564,7
0,4L	1800,41	30,35	1801,18
0,5L	1880,16	0	1880,16

Проверим местные нормальные напряжения на верхней кромке вертикального листа под сосредоточенной нагрузкой по формуле:

где z – длина верхней кромки вертикального листа, воспринимающая сосредоточенное усилие (рисунок 1.10);

R_см – расчетное сопротивление смятия (таблица 1.2).

Рисунок 1.10 – Схема распределения _

Длинна верхней кромки z определяется по формуле:

где J_ж – момент инерции полки вместе с рельсом относительно оси, проходящей через их общий центр тяжести (рисунок 1.11).

В качестве рельса применяем стандартный прокатный профиль квадратного сечения с размерами 4×4 см.

Рисунок 1.11 – Схема определения J_ж

Для определения положения общего центра тяжести составим систему уравнений:

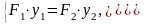
Решая полученную систему, определим расстояния y₁ и y₂:

y₁ = 2,534 – y₂;

16 · (2,534 – y₂) = 21,36 · y₂;

откуда y₂ = 1,085 см и y₁ = 1,448 см.

Тогда J_ж определится как:

+ 21,36 · 1,07 · 1,085² = 83,97 см⁴.

В итоге имеем:

≈ 15 см;

кг/см²  R_см = 3200 кг/см². Условие прочности выполняется.

1.6 Проверка общей устойчивости балки

Для проверки общей устойчивости балки вычислим коэффициент уменьшения допускаемых напряжений по формуле:

где J_x, J_y – моменты инерции сечения балки относительно соответствующих осей x и y;

h – высота балки;

l₀ – пролет балки или расстояние между закреплениями препятствующими перемещениям в горизонтальной плоскости.

Значение l₀ определяется исходя из ширины горизонтального листа:

l₀ = (10…20) · b_г = 15 · 21,36 = 320,0 см.

Моменты инерции определим как сумму моментов инерции горизонтальных листов и момента инерции вертикального листа относительно соответствующих осей:

см⁴;

см⁴.

Коэффициент ψ = f (α) определяется по графику в зависимости от параметра α (рисунок 1.12).

Рисунок 1.12 – Зависимость ψ = f (α)

Параметр α определяется по формуле:

Для заданной балки получаем:

Принимаем: α = 1, ψ = 1,85.

В итоге имеем:

Так как φ = 2,78 > 1,55, то для дальнейших расчетов принимаем φ = 1,00.

Проверка напряжений в балке с учетом требований обеспечения общей устойчивости проводится по формуле:

φ · R = 1 · 2100 = 2100 кг/см².

Так как _max = 1912,9 кг/см²  φ · R = 2100 кг/см², то устойчивость балки обеспечена.

1.7 Проверка устойчивости элементов балки

Местная устойчивость полок сжатого пояса не проверяется в связи с тем, что их ширина была принята b_г ≤ 20 · s_г.

1. Проверка необходимости постановки продольных ребер жесткости.

Установка продольных ребер жесткости необходима, если условная гибкость стенки

где k_кр = 160 – для малоуглеродистой стали.

 k_кр = 160 – постановка продольных ребер жесткости не требуется.

2. Расстановка вертикальных ребер жесткости.

Расстановка вертикальных ребер жесткости может быть специальная и обычная.

Специальная (достаточно частая) расстановка вертикальных ребер обусловлена потерей устойчивости вертикальной стенки при совместном действии нормальных и касательных напряжений. Необходимость специальной расстановки определяется из условия, что при динамических нагрузках k_y > k_кр^*. Для малоуглеродистой стали k_кр^* = 80.

Так как k_y = 136,51 > k_кр^* = 80, то требуется специальная расстановка ребер жесткости.

Нормальное напряжение на уровне верхней кромки вертикального листа в сечении, где действует максимальный изгибающий момент, определяется по формуле:

Тогда

кг/см².

Среднее касательное напряжение в сечении, где действует максимальная перерезывающая сила:

Тогда

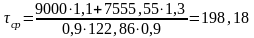кг/см².

Вычислим напряжение:

кг/см²_.

Вычислим напряжение ₀, приняв некоторое расстояние между ребрами жесткости а = 1,5 · h_в = 1,5 · 122,86 = 184,29 см:

где v – отношение большей из сторон ячейки к меньшей (а / h_в или h_в / а);

d – наименьшая из сторон ячейки a и h_в, заключенная между полками и осями ребер жесткости (рисунок 1.13).

Рисунок 1.13 – Схема ячейки между ребрами жесткости

Тогда имеем:

v = а / h_в = 184,29 / 122,86 = 1,5;

d = 122,86 см;

кг/см².

Вычислим напряжение:

где k₁ – коэффициент, определяемый по графику (рисунок 1.14).

Рисунок 1.14 – Зависимость k₁ = f (а / h_в)

Принимаем k₁ ≈ 9.

Тогда:

кг/см².

Проверим выполнение условия устойчивости:

В данном случае имеем:

- условие устойчивости выполнено.

Схема расстановки промежуточных вертикальных ребер жесткости показана на рисунке 1.15.

Рисунок 1.15 – Схема расстановки промежуточных ребер

Количество пар промежуточных ребер n_пр.р с округлением в большую сторону равно:

где L^* = L – 2 · l.

Расстояние от торца балки до оси опорного ребра l для балок из малоуглеродистой стали определяется по зависимости l = 15 · s_в.

Тогда имеем:

l = 15 · 0,9 = 13,5 см.

L^* = 1800 – 2 · 13,5 = 1773 см.

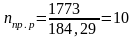шт.

Ширина промежуточного ребра:

см.

Толщина промежуточного ребра:

= 0,54 ≈ 0,6 см.