Для нашего ряда

Т.к. подозрительным результатом является В, то

Берем V₁₀ по абсолютной величине, т.е. равным и обращаемся к таблице 2 Приложения. При n = 8 и всех значениях доверительной вероятности Р

поэтому U₁₀ отбрасывается, как грубая погрешность или промах.

ж) В этот ряд нужно ввести поправку, обусловленную конечным сопротивлением вольтметра. Относительная погрешность измерения напряжения (методическая погрешность) для этого случая равная:

, откуда ,

где R – сопротивление участка, - сопротивление вольтметра. Поправка ; .

Получим значения поправок для каждого наблюдения и результаты наблюдений .

С учетом поправок ряд наблюдений примет вид: 26,11; 25,94; 26,13; 26,17; 25,96; 26,18; 26,25.

з) Определим для этого исправленного ряда среднее арифметическое

.

Остаточные суммы равны ; ; ; ; .

и) Поскольку ряд наблюдений подчиняется распределению Стьюдента, то вводим коэффициент t для вычисления величины доверительного интервала. Вероятность выбираем равной заданной, т.е. Р = 0,95.

.

Этот доверительный интервал ± = 0,08 В обусловлен случайными погрешностями измерений.

к) Однако, следует учесть и систематические погрешности.

Приборная систематическая погрешность обусловлена основной погрешностью вольтметра и определяется через класс точности прибора

.

Температурная систематическая погрешность обусловлена отклонением температурных условий от нормальных и по условию задачи равна

.

Магнитная систематическая погрешность по условию задачи равна

.

л) Суммарная неисключенная систематическая погрешность может быть найдена геометрическим суммированием (при доверительной вероятности Р = 0,95)

.

м) Проверим соотношения или . .

Данное отношение 4,85 не соответствует ни одному из соотношений, приведенных выше. Поэтому нужно суммировать случайные и систематические погрешности по формулам

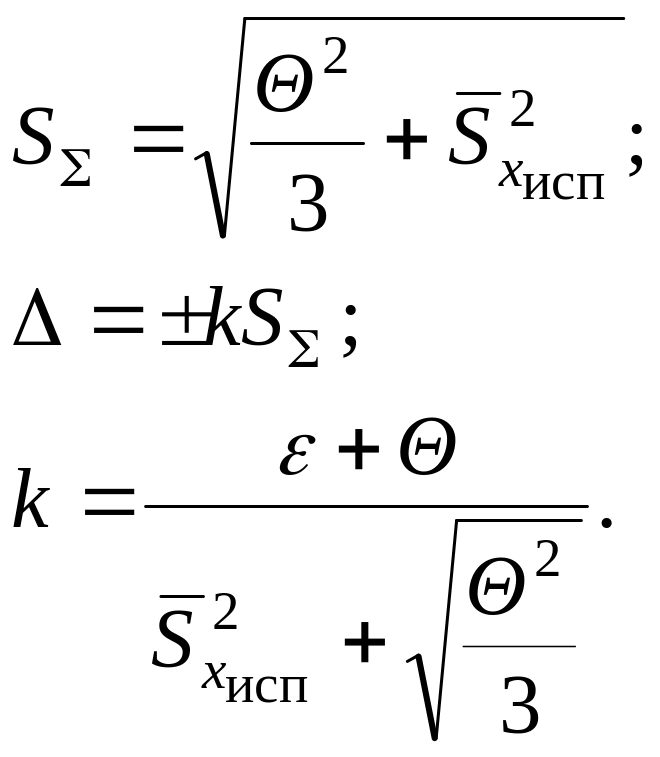
Вычисляем:

Суммарная погрешность

С учетом округления результат запишется в виде

203. Электродинамическим вольтметром класса точности 0,5 и номинальным значением 15 В измеряется ЭДС источника с внутренним сопротивлением . Сопротивление вольтметра 1500 кОм. Измерения проводились при температуре 25⁰С и воздействии магнитного поля свыше 400 А/м. Из паспортных данных прибора известно, что температурная погрешность вольтметра равна 20%, а магнитная погрешность 35% от основной погрешности. Получен ряд наблюдений: 11,95; 11,98; 12,05; 12,10; 12,15; 11,85; 12,07; 11,89; 12,00; 11,50 В.

Следует считать, что ряд наблюдений подчиняется распределению Стьюдента. Проверить, нет ли в ряду наблюдений промахов. Найти результат измерений и доверительный интервал результата при доверительной вероятности Р = 0,95.

203. При измерении тока среднее квадратическое отклонение составило 0,2% ( ).

Определить вероятность того, что случайная погрешность измерения будет лежать в пределах доверительного интервала .

Решение:

Границы доверительного интервала ; ; .

Для Z = 2,5 (определяется по таблице 3 Приложения). Таким образом, вероятность этого события Р = 0,9876. Уровень значимости: 1 - ; 1- 0,9876 = 0,0124 = 1,24%.

203. При измерении тока в цепи получен ряд результатов при постоянной нагрузке и напряжении: 12,992; 12,995; 12,997; 12,999; 12,00; 12,001; 12,003; 12,005; 12,007; 12,121 А.

Подозрительным является результат . Определить, является ли он промахом?

Решение:

Среднее значение тока в цепи равно

.

Оценка среднего квадратического отклонения результатов ряда

При n = 10 и всех значениях доверительной вероятности Р_дов как следует из таблицы 2 Приложения . Поэтому отбрасывается, как грубая погрешность (промах) и ряд подвергается новой обработке при n = 9.

203. При измерении электрической мощности при постоянной нагрузке среднее квадратическое отклонение результатов составило 0,5%.

Определить вероятность и уровень значимости того, что случайная погрешность измерения мощности будет лежать в пределах интервала .

203. При измерении падения напряжения на сопротивлении R были получены результаты: 6,53; 6,58; 6,49; 6,26: 6,60; 6,59; 6,19; 6,65; 6,71; 6,68 В.

Определить, если в этом ряду измерений промах?

203. Сопротивление в цепи постоянного тока измеряется методом амперметра и вольтметра. Температура измерения 25⁰С. Используются приборы МЭ системы. Показания амперметра: 1,68; 1,66; 1,63; 1,62; 1,64; 1,67; 1,68; 1,63; 1,65 А. Номинальное значение амперметра ; класс точности .

Показания вольтметра: 21,1; 21,2; 20,8; 20,9; 21,3; 21,5; 21,4; 20,7; 20,5 В. Номинальное значение В, класс точности . Сопротивление рамки амперметра, намотанной медным проводом 50 Ом; сопротивление добавочного резистора в комбинированном шунте амперметра 500 Ом; сопротивление шунта  0,6 Ом. Температурной погрешностью вольтметра можно пренебречь. Влияние магнитного поля на измерения ничтожно мало. Считать, что данные рядов измерений подчиняются распределению Стьюдента.

Определить результат измерения сопротивления и его погрешность при доверительной вероятности Р = 0,95. Коэффициент Стьюдента .

Схема измерения, рис. 81.

Решение:

Определим случайную погрешность результата.

Ее можно определить, исходя из формулы , где - оценка среднего квадратического отклонения среднего арифметического значения результатов; - коэффициент Стьюдента.

Поскольку измерения косвенные , то для расчета воспользуемся формулой

Для нахождения и - оценок средних квадратических отклонений средних арифметических показаний приборов найдем:

1. Средние арифметические значения показаний приборов

2. Определим среднее значение :

3. Найдем остаточные суммы рядов измерений и , получим:

и т.д.

В.

4. Определим и по формулам

5. Найдем

Случайная составляющая результирующей погрешности измерений будет равна

здесь t = 2,26 коэффициент Стьюдента, найденный по таблице 1 Приложения для n = 9 и Р = 0,95.

Найдем суммарную систематическую погрешность и введем поправки.

Согласно схеме измерений результат завышен на величину сопротивления амперметра = 0,6 Ом, т.е. ; = 12,77- 0,6 = 12,17 Ом.

Таким образом, поправка введена.

Систематические погрешности обусловлены классами точности приборов (т.е. основными погрешностями приборов) и влиянием температуры на показание амперметра. Остальными погрешностями можно пренебречь по условию задачи.

Температурная погрешность амперметра

где - сопротивление рамки амперметра; = 25⁰ – 20⁰ = 5⁰ – отклонение температуры от нормальной; - величина добавочного сопротивления в комбинированном шунте; - температурный коэффициент сопротивления медной проволоки, из которой намотана рамка амперметра, ;

Погрешность, обусловленная классами точности приборов (основная), может быть вычислена из соотношения

где ; ; и - классы точности амперметра и вольтметра; и их номинальные значения.

Суммарная неисключенная относительная систематическая погрешность измерений будет равна (с вероятностью Р = 0,95)

Абсолютная систематическая неисключенная погрешность будет иметь значение

Найдем отношение абсолютных неисключенной систематической и случайной погрешностей:

Так как это отношение меньше чем 0,8, то за величину погрешности результата можно принять значение , т.е. Ом. Результат измерения запишется в виде

203. Сопротивление в цепи измеряется методом амперметра и вольтметра при температуре 25⁰С. Остальные условия нормальные. Показания вольтметра:

21,5

21,7

22,4

22,5

23,3

21,9

21,8

22,2

22,1

Номинальное значение вольтметра В, класс точности 0,5, сопротивление вольтметра Ом.

Показания амперметра:

1,65

1,63

1,68

1,67

1,64

1,62

1,63

1,66

1,68

Номинальное значение амперметра ,5 А, класс точности 0,5. Сопротивление рамки амперметра 50 Ом, сопротивление добавочного резистора Ом.

Определить результат измерения сопротивления и его погрешность при доверительной вероятности Р = 0,95. Коэффициент Стьюдента принять равным . Распределение результатов подчиняется распределению Стьюдента.

Схема измерения, рис. 82.

Рис. 82.

203. Мощность в цепи измеряется методом амперметра и вольтметра в нормальных условиях. Показания вольтметра:

28,7

29,4

29,5

29,3

28,9

28,8

29,2

29,2

29,1

28,5

Номинальное значение вольтметра В, класс точности 1,5.

Показания амперметра:

0,62

0,63

0,66

0,68

0,65

0,63

0,68

0,67

0,64

0,64

Номинальное значение амперметра А, класс точности 2,5, сопротивление амперметра Ом.

Определить мощность, выделяющуюся на сопротивлении r_x и погрешность ее измерения при доверительной вероятности Р = 0,95. Коэффициент Стьюдента принять равным .

Схема измерения, рис. 83

Рис. 83.

203. Мощность в цепи измеряется методом амперметра и вольтметра в нормальных условиях. Показания вольтметра:

38,7

39,4

39,5

39,3

38,9

38,8

39,2

39,3

39,1

38,5

Номинальное значение вольтметра В, класс точности 1, сопротивление вольтметра Ом.

Показания амперметра:

0,64

0,67

0,68

0,63

0,65

0,62

0,63

0,62

0,66

0,68

Номинальное значение амперметра ,5 А, класс точности 1,5.

Определить мощность, выделяющуюся на сопротивлении r_x и погрешность ее измерения при доверительной вероятности Р = 0,95. Коэффициент Стьюдента принять равным .

Схема измерения, рис. 84.

Рис. 84.