1. Негізгі формулалар

Аргументтерді қосу формулалары:

a). sin(α+β)= sinα⋅cosβ + cosα⋅sinβ                                  b). cos(α+β)= cosα⋅cosβ -sinα⋅sinβ

c). sin(α-β)= sinα⋅cosβ -cosα⋅sinβ                                     d). cos(α-β)= cosα⋅cosβ + sinα⋅sinβ

e). tg(α+β)=                                                        f). tg(α-β)= 

 

Келтіру формулалары

2) Көпжақтар және оның элементтері

Анықтама 1. Егер көпжақты бұрыш өзінің жағын қамтитын әрбір жазықтыққа қарағанда сол жазықтықтың бір жағында орналасса, онда ол дөңес көпжақты бұрыш деп аталады.

Теорема 1. Үшжақты бұрыштың әрбір жазық бұрышы қалған екі жазық бұрышының қосындысынан кіші болады.

Теорема 2. Дөңес көпжақты бұрыштың барлық жазық бұрышының қосындысы -тан кіші болады.

Анықтама 2. Беті саны шектеулі көпбұрыштардың бірігуінен тұратын денені көпжақ деп аталады.

Анықтама 3. Егер көпжақ өзінің жағын қамтитын жазықтықтардың кез келгеніне қарағанда тұтастай бір жақ бетінде орналасса, онда ол дөңес көпжақ деп аталады.

Көпжақтың бетін құрайтын көпбұрыштар көпжақтың жақтары деп, жақтардың ортақ қабырғалары қырлары, қырларының ортақ нүктелері төбелері деп аталады. Көпжақтың оның барлық төбелерін көрсететін әріптермен белгілейді.

Көпжақтың бір жағында жатпайтын екі төбесін қосатын кесіндіні көпжақтың диагоналі дейді.

2. Тік және дұрыс призма.

Анықтама 1. Бүйір қырлары табандарына перпендикуляр призмалар тік призмалар деп аталады.

Анықтама 2. Әрі тік, әрі табаны дұрыс көпбұрыш болатын призманы дұрыс призма деп атайды.

№7 билет

1. Функция графигіне жүргізілген жанаманың теңдеуі.

2. Жазықтық пен түзудің және жазықтықтардың перпендикулярлығы.

1. Жанаманың теңдеуі

 

             y=f(x) функциясы Nₒ(xₒ;yₒ) нүктесіндегі f ʹ(xₒ) берілсін.

Жанаманың теңдеуі түзу болғандықтан y=kx+b сызықтық функция ретінде іздейміз. Мұндағы k=tgα= f ʹ(xₒ), бұдан  y= f ʹ(xₒ) x+b.

Nₒ(xₒ;f (xₒ) ) нүктесінің координаталарын қоямыз бұдан f (xₒ)= f ʹ(xₒ) xₒ+b

f (xₒ)= f ʹ(xₒ) xₒ+b теңдеуінен b-ны табамыз: b = f (xₒ)- f ʹ(xₒ) xₒ

b = f (xₒ)- f ʹ(xₒ) xₒ теңдеуін y= f ʹ(xₒ) x+b теңдеуіне қоямыз:

 y= f ʹ(xₒ) x+ f (xₒ)- f ʹ(xₒ) xₒ.  Соңғы теңдеуді ықшамдау арқылы:   y= f (xₒ)+ f ʹ(xₒ) — (x — xₒ)  аламыз. Бұл жанаманың теңдеуі.

 ЖАНАМАНЫҢ ТЕҢДЕУІН ЖАЗУ АЛГОРИТМІ

• xₒ -ге сәйкес  f (xₒ)—ді есептеу.

• f (x) функциясының туындысын табу.

• xₒ—дегі туындының мәні f ʹ(xₒ)—ді есептеу.

• y= f (xₒ)+ f ʹ(xₒ) ·(x — xₒ) формуласына қойып жанаманың теңдеуін алу.

1-мысал: f (x)=x²-5x+6 функциясының xₒ=1 нүктесіндегі жанаманың теңдеуін жазыңыз.

• f (xₒ) =f(1)=1²-5·1+6=2.

• f ʹ(x)=2x-5.

• f ʹ(xₒ)= f ʹ(1)=2·1-5=-3

• y= f (xₒ)+ f ʹ(xₒ) ·(x — xₒ) =2-3(x-1)=2-3x+3=5-3x.

Бұдан жанаманың теңдеуі: y=5-3x

2. Жазықтыққа перпендикуляр түзу

Теорема №1 Түзу жазықтыққа перпендикуляр болуы үшін , ол осы жазықтықта қиылысқан екі түзуге перпендикуляр болуы керек.

3. 

4. A  , b  

5. l  

   a  b = K

6. l  a

7. l  b

Теорема №2. Егер түзудің нақты шамасы жазықтық ізіне перпендикуляр болса, онда түзу кеңістікте берілген жазықтыққа перпендикуляр.

8. 

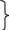10. l"  ₂ ,

11. ₂ – жазықтықтың фронтальізі, l  

12. l" – Н.Ш.

15. 

Теорема №3. Егер түзудің горизонталь проекциясы горизонтальдің горизонталь проекциясына немесе жазықтықтың горизонталь ізіне перпендикуляр болса, ал оның фронталь проекциясы фронтальдің фронталь проекциясына немесе жазықтықтың фронталь ізіне перпендикуляр болса, онда түзу жазықтыққа перпендикуляр.

f  S , h  S

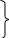
l ^S

l"  f"

l'  h'

№8 билет

1. N- ші дәрежелі түбір және оның қасиеттері.

2. Тік дөңгелек цилиндр және оның элементтері.

Анықтама: а –санының n-ші дәрежелі түбірі деп n-ші дәрежесі а санына тең болатын в санын айтамыз Мұндағы а саны n-ші дәрежелі түбірі таңбасының ішіндегі сан, n –түбірдің  көрсеткіші және , в саны а санының n-ші дәрежелі түбірі Мысалы: 64 санының үшінші дәрежелі түбірі 4 –ке тең. n-ші дәрежелі түбір анықтамасындағы түбір көрсеткішінің жұп және тақ болатын жағдайларын жеке қарастырамыз. N жұп сан болса, онда , тек қана оң сан, себебі кез-келген санның жұп дәрежесі оң сан немесе 0. Демек, жұп дәрежелі түбір таңбасының  ішіндегі а саны теріс сан болуы мүмкін емес. Егер түбір көрсеткіші n тақ сан болса, онда кез-келген саннан n-ші дәрежелі Түбірді есептеуге болады.Бұл жағдайда теңдігіндегі а және в  сандарының таңбалары бірдей, яғни оң саннан оң, теріс саннан теріс түбір шығады.  Анықтама: Теріс емес а санының n-ші дәрежелі арифметикалық түбірі деп  n-ші дәрежесі а санына тең болатын теріс емес в санын айтады.  және болғанда, а және в теріс емес нақты сандары үшін n-ші және k-ші дәрежелі түбірлердің мына қасиеттері орындалады: Берілген n-ші дәрежелі түбірдің қасиеттерін дәрежелеу және түбір табу амалдарының анықтамаларын пайдаланып дәлелдеуге болады.

1. Цилиндр деп тік төртбұрышты оның қабырғаларының бірінен айналдырғанда шығатын фигураны атайды.

Егер жасаушылары цилиндрдің табандарына перпендикуляр, яғни цилиндрдің биіктігіне тең болса, онда цилиндр тік дөңгелек цилиндр деп аталады.

№9 билет