№1 билет

1. Қарапайым көрсеткіштік теңсіздікті шешу.

2. Жазықтықтағы фигуралардың ауданы. Тік төртбұрыш, квадрат, үшбұрыш,трапеция, дөңгелек және параллелограмм

1. Анықтама: Айнымалысы дәреженің көрсеткішінде болатын теңсіздікті көрсеткішті теңсіздік деп атайды.  a f(x) ≥ a g(x) теңсіздігі көрсеткіштік теңсіздік деп аталады.

Бұл теңсіздік мына теңсіздіктерге эквивалентті:  1). a > 1 болса онда f(x) ≥ g(x)  2). 1> a > 0 болса онда f(x) ≤ g(x)  Мысалы (бірінші мысал) 32x ≥ 3x+1 теңсіздігін шешейік:  32x ≥ 3x+1  3>1  2x ≥ x+1 (сызықты теңсіздіктер)  2x-x ≥ 1  x ≥ 1  Жауабы: x ≥ 1.

2).

1) Бер: АВСД тіктөртбұрыш

АВ =242,5 м

ВС= 81,6 м в

Т/к: S =?

Т/ү: S =ав а

S = 242,5 ∙ 81,6=19788 м²

Жауабы: 19788 м 2 =1,9788 га

19788 м 2 =197,88 ар

2) Трапеция (от көне грекше: τράπέζιου — «үстел»; τράπεζα — «дастарқан, ас, тамақ») деп тек қарама – қарсы екі қабырғасы параллель төртбұрышты айтады.

Параллель қабырғалары трапецияның табандары деп аталады, басқа екі қабырғасы бүйір қабырғалары деп аталады, ал бүйір қабырғаларының орталарын қосатын кесіндіні трапецияның орта сызығы деп атайды.

Трапецияның қасиеттері

1. Трапецияның орта сызығы оның табандарына параллель және сол табандардың қосындысының жартысына тең болады.

2. Егер трапеция тең бүйірлі болса онда оның диагональдары және табанындағы бұрыштары тең болады.

3. Егер трапеция тең бүйірлі болса, онда оған сырттай шеңбер сызуға болады.

4. (3-ке кері.) Егер трапецияға сырттай шеңбер сызуға болатын болса, онда ол тең бүйірлі.

{\displaystyle m={\frac {1}{2}}(a+b).}

Трапеция ауданы былай есептеледі

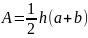
Ал орта сызығы

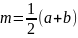
3) Үшбұрыштың ауданы оның қабырғасы мен сол қабырғаға түсірілген биіктігі көбейтіндісінің жартысына тең. Яғни

S=1/2 · ah

формуласымен есептеледі, мұндағы a - үшбұрыштың қабырғасы, h - сол қабырғаға түсірілген биіктік.

Үшбұрыштың ауданын табудың басқа да формулалары бар:

Үшбұрыштың ауданы оның екі қабырғасы мен осы қабырғалар арасындағы бұрыштың синусы көбейтіндісінің жартысына тең. Яғни S=1/2 · ah sin γ формуласымен есептеледі, γ - олардың арасындағы бұрыш.

Келесі формула Ӏ ғасырда Александрия қаласында өмір сүрген ертедегі грек ғалымы Геронның атымен аталады. Егер үш қабырғасы белгілі болса, үшбұрыштың ауданын Герон формуласымен есептеуге болады:

S=√p(p-a)(p-b)(p-c)

мұндағы a,b,c - үшбұрыштың қабырғалары, ал p - оның жарты преиметрі яғни: p=a+b+c/2

4) Шеңбер

Шеңбер– барлық нүктесі берілген нүктеден (шеңбер орталығынен) бірдей қашықтықта жататын тұйық қисық сызық. Шеңбер центрін оның кез келген нүктесімен қосатын R кесіндісі (немесе осы кесіндінің ұзындығы) шеңбер радиусы деп аталады. Шеңбер ұзындығының оның диаметріне қатынасы тұрақты сан (барлық шеңбер үшін бірдей) болады. Бұл қатынас гректің π=3,14159… (қ. Пи саны) әрпімен белгіленеді. π саны трансцендент санға жатады. Шеңбер ұзындығы L=2πR формуласымен анықталады. Жазықтықтың шеңбермен шектелген және орталығы бар бөлігі дөңгелек аталады; дөңгелектің ауданы S=πR²-қа тең.

5) Параллелограмм – қарама-қарсы қабырғалары параллель болатын, яғни параллель түзулердің бойында орналасқан төртбұрыш.

Параллелограммның қасиеттері

1. Қарама – қарсы қабырғалары тең. : {\displaystyle |AB|=|CD|}, {\displaystyle |AD|=|BC|}.

2. Қарсы жатқан бұрыштары тең. : {\displaystyle \angle A=\angle C,\angle B=\angle D.}

3. Диагональдары қиылысады және қиылысу нүктесінде қақ бөлінеді. : {\displaystyle |AO|=|OC|}, {\displaystyle |BO|=|OD|}.

4. Бұрыштарының іргелес біржақты жатқан қабырғаларының қосындысы 180º-қа тең.

5. Диагональдарының квадраттарының қосындысы оның барлық қабырғаларының квадраттарының қосындысына тең.

{\displaystyle d_{1}^{2}+d_{2}^{2}=2(a^{2}+b^{2}).}Параллелограммның белгілері

Егер мына шарттар орындалса онда төртбұрыш параллелограмм болады:

1. Қарама – қарсы қабырғалары тең және параллель (|AB| = |CD|, |AD| = |BC|)

2. Қарама – қарсы қабырғалары қос – қостан тең (|AB| = |CD|, AB || CD).

3. Қарама – қарсы бұрыштары қос – қостан тең (∠A = ∠C, ∠B = ∠D).

4. Диагональдары қиылысу нүктесінде қақ бөлінеді (|AO| = |OC|, |BO| = |OD|).

№2 билет

1. Нақты көрсеткішті дәрежелік функцияның туындысы мен интегралы.

2. Үш перпендикуляр туралы теорема.

1. Туындының формуласы:

Мұндағы n – бүтін сан.

Мысалы:

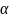кез келген нақты сан болса, онда 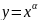дәрежелік функциясының туындысы

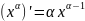
Формуласымен есептелінеді.

Мысалы: 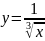функциясының туындысын табайық.

Жауабы: .

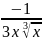функциясының алғашқы функциясы

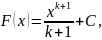мұндағы k – кез келген бүтін сан.

Кез келген нақты сан үшін дәрежелік функцияның интегралы мына формуламен анықталады:

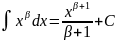
Мысалы: 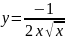функциясының 1-ден 4-ке дейінгі анықталған интегралын есептейік.

Шешуі:

=

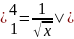
Жауабы: