Файлы для подготовки к экзамену / О методах и алгоритмах параллельного решения задач и их характеристиках

1.2.2. О методах и алгоритмах параллельного решения задач и их характеристиках

Процесс программирования можно рассматривать как многоэтапный переход от задачи к представлению выбранного метода и способа ее решения на конкретном языке программирования [1, 2]. Показатели, характеризующие качество разработанной программы, степень достижения предъявляемых к программе требований (времени вычисления, объему требуемой памяти и др.) в большой степени определяются методом решения задачи, выбором языка программирования и собственно уровнем программистского искусства, которое заключается в умелом использовании языковых средств для точного представления метода решения задачи и построение эффективной программы.

Точность, зависящая от нее вычислительная сложность метода, в большой степени предопределяют качество разрабатываемой программы.

Для методов, которые предназначаются для параллельного решения задач, принципиальное значение имеет коэффициент ускорения, определяемый как отношение времени выполнения программы, реализующей метод, на одном компьютере, ко времени ее параллельного выполнения на ВС.

Пусть C(x₁, x₂, …, x_m, k) – функция, определяющая зависимость коэффициента ускорения от сложности задачи, характеризуемой параметрами x₁, x₂, …, x_m, и количества k компьютеров ВС, на которой выполняется параллельная программа, реализующая метод.

Для многих задач часто достаточно просто предельное значение C(x₁, x₂, …, x_m, k), если предполагать, что количество компьютеров или процессоров ВС не ограничено (в этом случае не возникает задержек при выполнении параллельной программы из-за отсутствия необходимых ресурсов) и не учитывать системные издержки на организацию выполнения параллельной программы на ВС (обменные взаимодействия, управление и др. [1, 2]).

Именно при этих предположениях обычно определяется коэффициент ускорения для многих методов параллельных программ.

В качестве параметров x₁, x₂, …, x_m, характеризующих вычислительную сложность задачи, во многих случаях используются параметры, определяющие размерность задачи. которые одновременно являются и аргументами программы, представляющей метод ее решения [1, 2].

Рассмотрим пример простой задачи вычисления значений n!, используя для этого параллельный метод разбиения отрезка [1n] пополам, по программе:

, где – ближайшее целое к a. Очевидно, F(1, n) = n!.

Если попытаться реализовать процесс вычисления значения n! по этой программе, используя все возникающие при этом возможности распараллеливания, нетрудно показать [11], что этот процесс следует очевидной схеме:

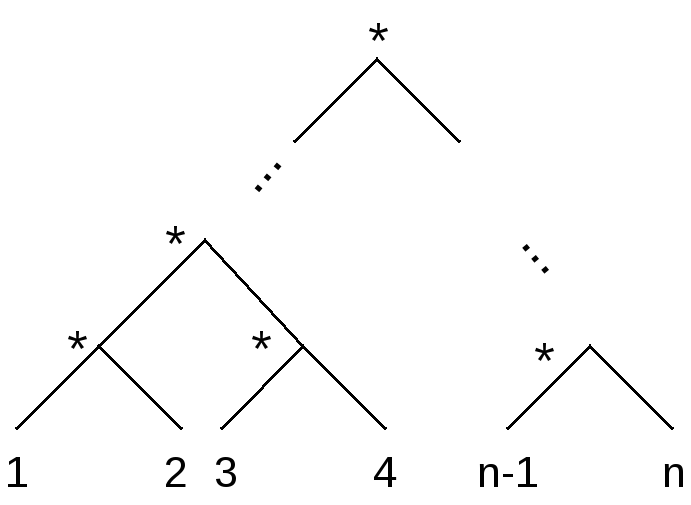
Параметр n – аргумент приведенной выше функции – характеризует вычислительную сложность задачи, а коэффициент C(n) (при неограниченном числе компьютеров ВС) ведет себя как 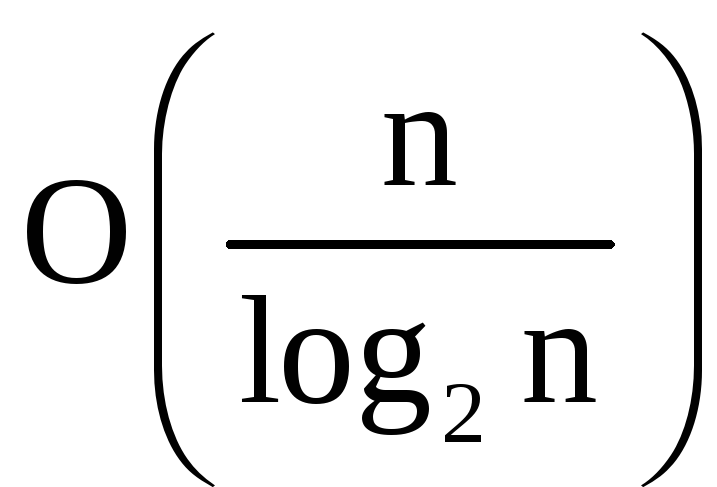и при неограниченном увеличении n стремится к бесконечности.

Таким образом, с усложнением задачи (увеличением n) можно неограниченно сокращать время выполнения этой программы при условии неограниченных ресурсов.

Можно привести множество примеров других задач (перемножение матриц, решение систем линейных уравнений, численное интегрирование и др.), для которых с увеличением их сложности коэффициент ускорения возрастает неограниченно.

Следуя закону Амдала, предельное ускорение решения задачи в параллельной форме равно:

,

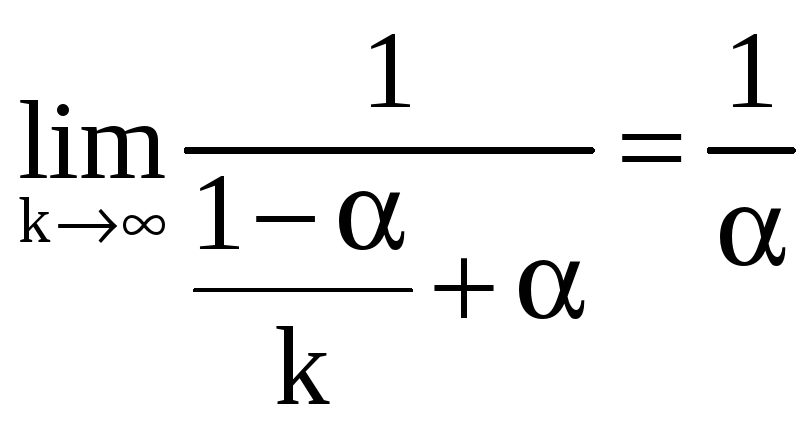где  – доля операций в программе решения задачи, которые выполняются последовательно ((1-) – доля параллельного выполняющихся операций), k – количество компьютеров ВС.

Для приведенного примера с ростом n доля последовательных операций, очевидно, стремится к нулевому значению.

В [1] введен еще один параметр, который определяет глубину распараллеливания метода (или представляющего его алгоритма) и который интуитивно характеризует в среднем вычислительную сложность компонентов параллельной программы, которые рассматриваются как самостоятельные ее части, которые могут выполняться одновременно.

Глубина распараллеливания формально отражает используемое в параллельном программировании понятие granularity (зернистость). Обозначим этот параметр d, а функцию, определяющую коэффициент ускорения будем обозначать C(x₁, x₂, …, x_m, d, k), вводя d в качестве ее параметра.

Обратную к d величину будем определять как степень распараллеливания, которая характеризует усредненное количество компонентов параллельной программы, выполняемых одновременно.

Рассмотрим простой пример перемножения квадратных матриц размера n и определим предельный коэффициент ускорения процесса параллельного решения этой задачи для различных d и неограниченного количества компьютеров в ВС.

1. d₁ – сложность вычисления одной строки результирующей матрицы, а степень распараллеливания – одновременное вычисления всех строк матрицы:

.

2. d₂ – сложность вычисления одного элемента результирующей матрицы, а степень распараллеливания – одновременное вычисление всех элементов результирующей матрицы:

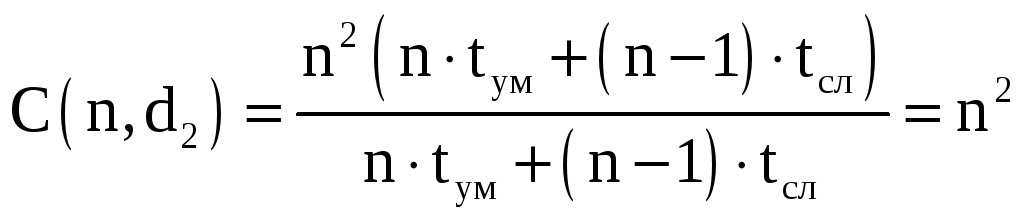
3. d₃ – сложность выполнения операции умножения, а степень распараллеливания – одновременное вычисление выполнение всех операций умножения при одновременном вычислении всех элементов результирующей матрицы:

,

где r₁ – некоторая константа, r₁1.

4. d₄ – усредненная сложность выполнения операции умножения и параллельного вычисления суммы 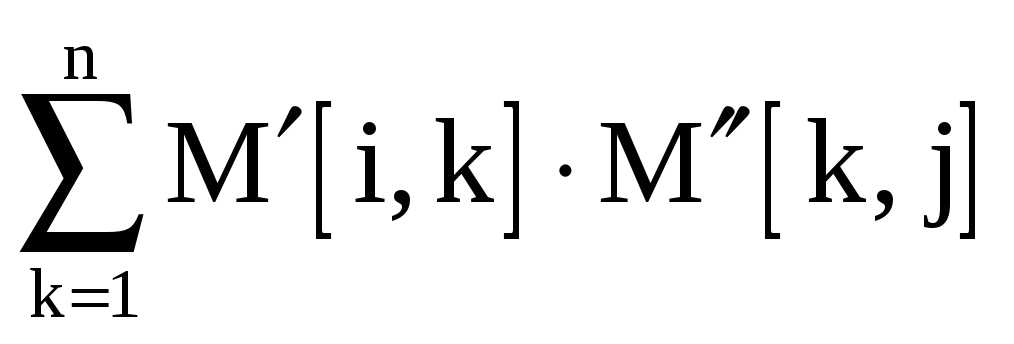, при вычислении элементов результирующей матрицы, степень распараллеливания определяется исходя из условия одновременного выполнения всех операций умножения при последующем параллельном вычислении приведенной выше суммы делением отрезка [1n] пополам (см. пример параллельного вычисления функции факториал выше):

,

где r₂1.

Нетрудно видеть, что во всех четырех случаях коэффициент ускорения неограниченно растет с увеличением n (в [1] такие алгоритмы отнесены к классу алгоритмов с неограниченным параллелизмом). Однако, производная (ускорение) этого роста различна для различных d, причем, например, для d₁, d₂, d₃ коэффициент ускорения растет как O(n), O(n²) и O(r₁n³) соответственно, увеличиваясь в n раз при уменьшении d.

Однако если перевести этот результат в практическую плоскость, реализуя параллельное вычисление произведения двух матриц на реальной ВС с реальной пропускной способностью сегодняшних каналов связи при сегодняшних технических характеристиках компьютеров (быстродействием процессора, временем обмена с дисковой памятью и др.), то можно наблюдать, что с увеличением степени распараллеливания (и достаточно большом качестве компьютеров в ВС) растет суммарное время, которое тратится на обменные взаимодействия и управление. Более того, для глубины распараллеливания d₃ и d₄ эти «накладные расходы» нивелируют эффект от распараллеливания [1].

Общий вывод состоит в том, что мало уметь строить «максимально» параллельные алгоритмы решения задач, необходимо также находить оптимальное значение глубины и степени распараллеливания при их реализации на ВС с учетом их технических характеристик [1].

В [2] введена еще одна характеристика параллельных алгоритмов – ширина максимального яруса при их выполнении, которая определяет наименьшее количество компьютеров ВС, которое позволяет выполнить параллельный алгоритм без задержек из-за отсутствия необходимых ресурсов. В общем случае этот параметр можно получить, анализируя трассу (историю) выполнения параллельного алгоритма на идеализированной ВС с неограниченным числом компьютеров.

Так, например, в [2] сравнивались параллельные алгоритмы численного интегрирования с равномерным и неравномерным шагом разбиения интервала интегрирования. Программа интегрирования функции f(x) с заданной точностью  на интервале [a, b] с неравномерным шагом разбиения весьма напоминает метод программы вычисления значения функции факториал делением отрезка [1, n] пополам:

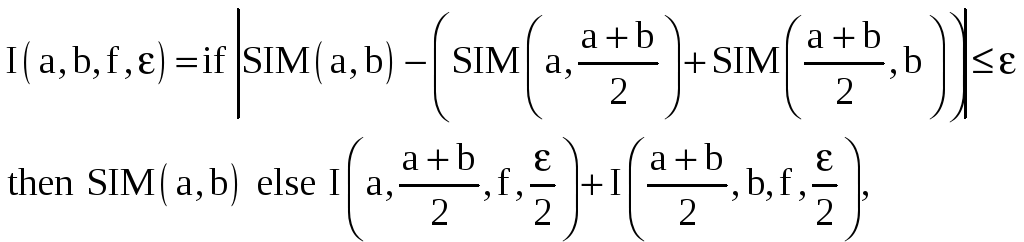
где SIM(x, y) – функция вычисления значения интеграла на отрезке [x, y] с использованием формулы Симпсона.

Известно, что эта функция обладает большей точностью по сравнению с алгоритмом интегрирования, основанном на стратегии равномерного разбиения интервала интегрирования:

,

где  – точность, а _r – значение интеграла для шага разбиения r.

В [2] приведены данные исследования обоих методов интегрирования, где показано, что ширина максимального яруса для случая неравномерного разбиения при вычислении интеграла для известных элементарных функций на несколько порядков меньше по сравнению с равномерным разбиением.

Как следствие, в первом случае потребуется на несколько порядков меньше компьютеров в ВС, чтобы реализовать заложенный в программе метод параллельно и без задержек из-за отсутствия должного количества ресурсов в ВС.

Очевидно, что на практике при организации параллельных вычислений важно знать не только коэффициент ускорения, получаемый при выполнении параллельной программы на реальной ВС (с заданным количеством компьютеров или процессоров и их характеристиками, включая быстродействие, объем оперативной памяти, пропускную способность каналов обмена и др.), но и то, как при этом используются ее ресурсы.

Для определения эффективности использования ресурсов обычно используют отношение C(x₁, x₂, …, x_m, k)/k,причем часто считают, что это отношение не может быть больше единицы, полагая, что ускорение не может быть больше k – количества компьютеров ВС.

В действительности, это не так, поскольку для сложных задач, требующих большого объема памяти, ускорение может быть больше k. Это связано с тем, что на одном компьютере (предполагая, что его память не больше объема памяти всех компьютеров ВС) из-за большой интенсивности обменов между оперативной памятью и дисками коэффициент ускорения может быть больше k. Это в реальности наблюдается даже на простых задачах перемножения матриц и решения систем линейных уравнений большого размера [2].

Интересно проследить общий характер изменения показателя эффективности использования ресурсов ВС для задачи заданной сложности с увеличением k – количества компьютеров (процессоров) ВС.

Очевидно, если не изменяется глубина распараллеливания и сохраняется общая схема организации выполнения параллельной программы на ВС, этот показатель сначала должен увеличиваться (точнее, не уменьшаться) с увеличением k при выполнении параллельной программы заданной сложности. Однако, всегда будет существовать некоторое оптимальное значение k, увеличение которого уже не может уменьшить время выполнения программы (нужна задача большей сложности или требуется уменьшение глубины распараллеливания). Это вытекает из анализа изменения коэффициента ускорения в зависимости от k.

Общий вывод из изложенного в этом параграфе материала состоит в том, что при построении эффективных параллельных программ необходимо не только серьезное внимание уделять разработке параллельных методов решения задач, но и уметь их анализировать и «приспосабливать» к конкретной вычислительной аппаратуре (ВС) с тем, чтобы достигался максимальный эффект.

Литература к 1.2.1 и 1.2.2

1. Кутепов В.П. Об интеллектуальных компьютерах и больших компьютерных системах нового поколения // Изв. РАН. Теория и системы управления, 1996. №5.

2. Кутепов В.П. Организация параллельных вычислений на системах. – М.: МЭИ, 1988.

3. Хоар Ч. Взаимодействующие последовательные процессы. М.: Мир, 1989.

4. Milner R. A Calculus of Communicating Systems. Lecture Notes in Computer Science, vol. 92. Springer-Verlag, New York, 1980.

5. Кутепов В.П., Фальк В.Н. Функциональные системы: теоретический и практический аспекты // Кибернетика, 1979. №1.

6. Бажанов С.Е., Кутепов В.П., Шестаков Д.А. Язык функционального параллельного программирования и его реализация на кластерных системах. М.: Программирование (в печати).

7. Вагин В.Н. и др. Достоверный и правдоподобный вывод в интеллектуальных системах. М.: Физматлит, 2004.

8. Filman R.E., Friedman D.E. Coordinating computing tools and techniques for distributed software. McGraw-Hill, 1984.

9. Абрамов С.М. и др. Т-система с открытой архитектурой. Суперкомпьютерные системы и их применение. Международная научная конференция, Минск, 2004.

10. Котляров Д.В., Кутепов В.П., Осипов М.А. Граф-схемное потоковое параллельное программирование и его реализация на кластерных системах. Изв. РАН, Теория и системы управления, 2005, №1, Москва.

11. Эндрюс Г. Основы многопоточного, параллельного и распределенного программирования. – М.: Издательский дом «Вильямс», 2003.