
-
Чисто функциональный язык.
Язык
![]() -исчисления
(множество
-исчисления
(множество
![]() -термов)
есть подмножество термов языка
-термов)
есть подмножество термов языка
![]() ,
построенных без использования символов
присваивания, конструкций блоков и
рекурсивных процедур. Другими словами,
,
построенных без использования символов
присваивания, конструкций блоков и
рекурсивных процедур. Другими словами,
-
пустая строка есть
 -терм,
-терм, -
если
 –
–
 -терм,
то
-терм,
то
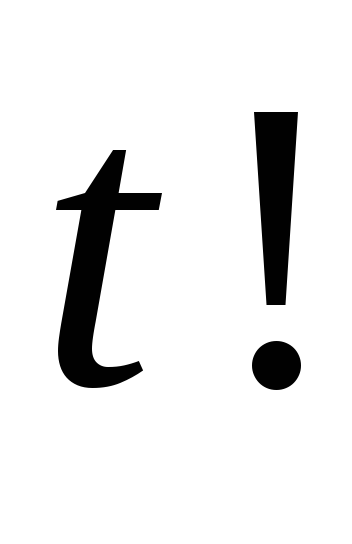 ,
,
 (для всех
(для всех
 )
–
)
–
 -термы,
-термы,
-
если
 и
и
 –
–
 -термы,
а
-термы,
а
 ,
то
,
то
 и
и
 –
–
 -термы,
-термы, -
других
 -термов,
не определенных п.п. 1-3, нет.
-термов,
не определенных п.п. 1-3, нет.
Практически
более удобным является другое определение
множества
![]()
![]() -термов:
-термов:
-
пустая строка есть
 -терм,
-терм, -
 и
и
 (для всех
(для всех
 )
–
)
–
 -термы,
-термы, -
если
 –
–
 -терм,
а
-терм,
а
 ,
то
,
то
 и
и
 –
–
 -термы,
-термы, -
если
 и
и
 –
–
 -термы,
то
-термы,
то
 –
–
 -терм,
-терм,
-
других
 -термов,
не определенных п.п. 1-4, нет.
-термов,
не определенных п.п. 1-4, нет.
Для
![]() -исчисления
определены правила
-исчисления
определены правила
![]() -редукции,
-редукции,
![]() -редукции
и
-редукции
и
![]() -конверсии
(здесь и далее
-конверсии
(здесь и далее
![]() ,
,
![]() ):
):
-
 ,
, -
 ,
, -
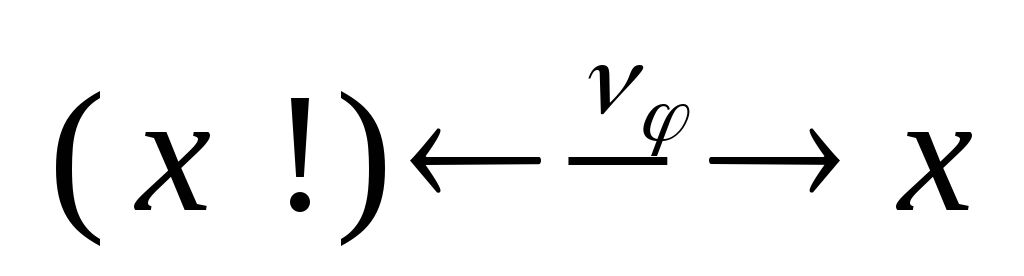 .
.
Отношение
![]() редукции на множестве
редукции на множестве
![]() -термов
определяется как рефлексивное и
транзитивное замыкание отношений
-термов
определяется как рефлексивное и
транзитивное замыкание отношений
![]() ,
,
![]() и
и
![]() ,
распространяемое на произвольные
контексты
,
распространяемое на произвольные
контексты
![]() -термов:
-термов:
-
 ,
, -
 ,
, -
 ,
, -
 ,
, -
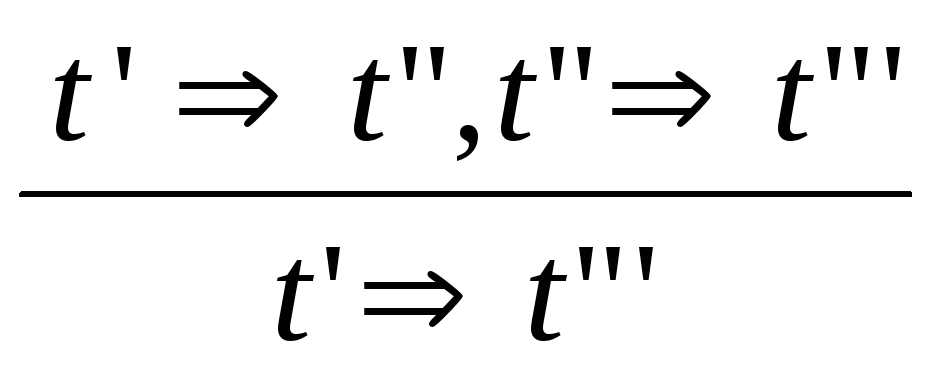 ,
, -
 ,
,
а
отношение
![]() конверсии как рефлексивное, транзитивное
и симметричное замыкание отношений
конверсии как рефлексивное, транзитивное
и симметричное замыкание отношений
![]() ,
,
![]() и
и
![]() ,
распространяемое на произвольные
контексты
,
распространяемое на произвольные
контексты
![]() -термов,
дополненное правилом экстенсиональности
(8):
-термов,
дополненное правилом экстенсиональности
(8):
-
 ,
, -
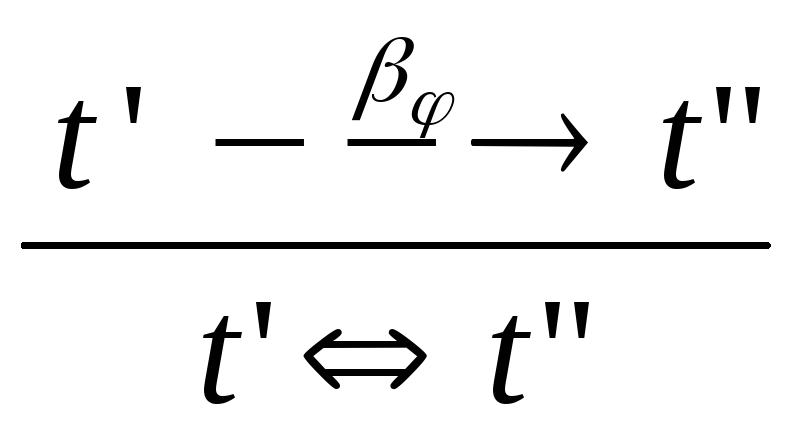 ,
, -
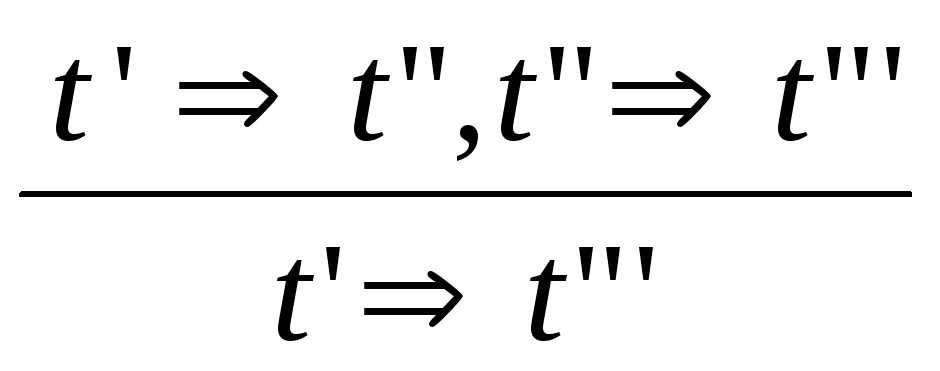 ,
, -
 ,
, -
 ,
, -
 ,
, -
 ,
, -
 .
.
Покажем,
например, что имеет место редукция:
![]()
![]() .
Действительно,
.
Действительно,
![]()
![]()
![]() и
и
![]() .
.
Отсюда
следует доказываемое утверждение.
Аналогично можно показать, что имеет
место и редукция
![]()
![]() .
.
Вторым
примером является доказательство
конверсии
![]() .
.
Действительно,
![]() ,
и далее искомый результат следует по
правилу экстенсиональности.
,
и далее искомый результат следует по
правилу экстенсиональности.
Третьим
примером является доказательство
редукции
![]()
![]() ,
известной как правило замены операторной
переменной:
,
известной как правило замены операторной
переменной:
Доказательство:
![]()
![]() .
.
Система
правил для строгого
![]() -исчисления
редукций без использования правила
экстенсиональности может выглядеть
так:
-исчисления
редукций без использования правила
экстенсиональности может выглядеть
так:
-
 ,
, -
 ,
, -
 ,
, -

 ,
, -
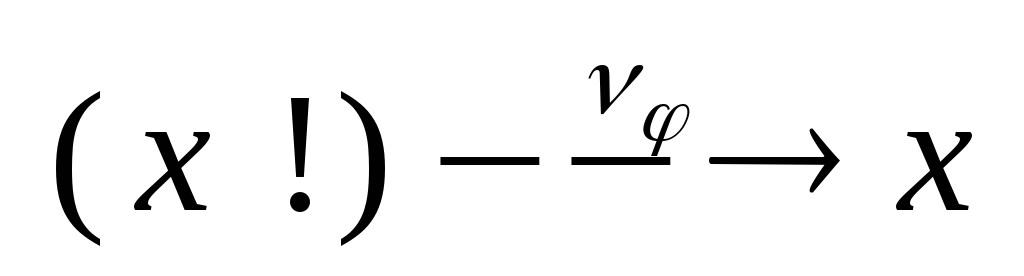 .
.
Термы
![]() -исчисления
строятся по тем же синтаксическим
правилам, что и
-исчисления
строятся по тем же синтаксическим
правилам, что и
![]() -термы,
за исключением константы
-термы,
за исключением константы
![]() ,
которая в
,
которая в
![]() -исчислении
вводится по определению:
-исчислении
вводится по определению:
![]() .
Трансляцию
.
Трансляцию
![]() -термов
в
-термов
в
![]() -исчисление
определим так:
-исчисление
определим так:
![]() ,
,
![]() ,
,
![]() ,
,
а
обратную трансляцию
![]() -термов
в
-термов
в
![]() -исчисление
так:
-исчисление
так:
![]() ,
,
![]() ,
,
![]() .
.
![]() -Исчисление
использует единственное правило
редукции:
-Исчисление
использует единственное правило
редукции:
![]() .
.
Отношения
![]() редукции и
редукции и
![]() конверсии на множестве
конверсии на множестве
![]() -термов
определяются так же, как и на множестве
-термов
определяются так же, как и на множестве
![]() -термов,
за исключением правила экстенсиональности,
которое выглядит так::
-термов,
за исключением правила экстенсиональности,
которое выглядит так::
-
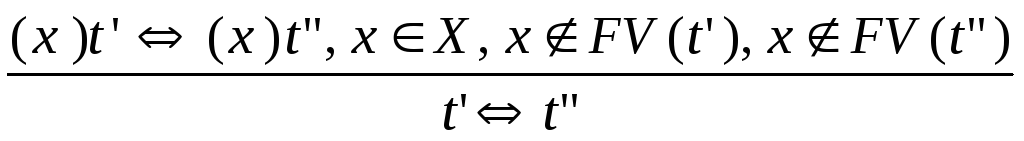 .
.
При
трансляции
![]() -термов
в
-термов
в
![]() -исчисление
правила редукции
-исчисление
правила редукции
![]() и
и
![]() становятся в нем выводимыми:
становятся в нем выводимыми:
![]() ,
,
![]() .
.
Определим
теперь правила трансляции
![]() -термов
в язык
-термов
в язык
![]() -исчисления
следующим образом (
-исчисления
следующим образом (![]() -терм
-терм
![]() будем называть
будем называть
![]() -образом
-образом
![]() -терма
-терма
![]() ):
):
![]() ,
,
![]() ,
,
![]() .
.
Очевидно,
что
![]() .
Тогда получим:
.
Тогда получим:
![]()
![]() Следовательно,
имеет место диаграмма
Следовательно,
имеет место диаграмма
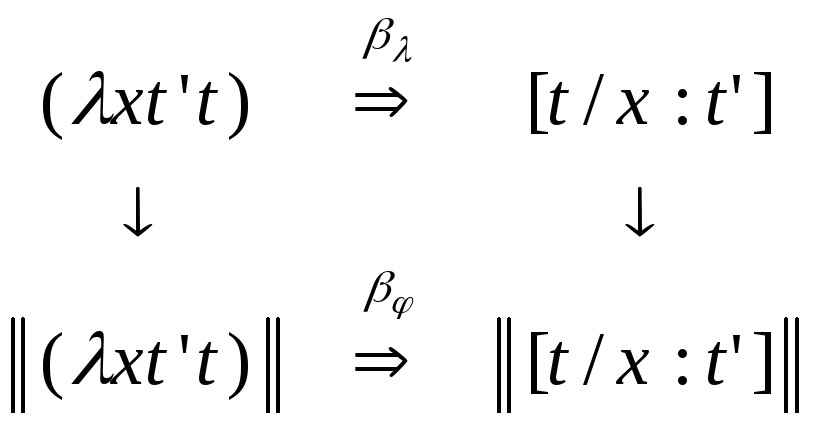 .
.
![]() -Правило
(правило замены операторной переменной)
одинаково имеют место и в
-Правило
(правило замены операторной переменной)
одинаково имеют место и в
![]() -исчислении,
и в
-исчислении,
и в
![]() -исчислении
(в нем оно выводимо). Очевидно и то, что
если
-исчислении
(в нем оно выводимо). Очевидно и то, что
если
![]() -терм
-терм
![]() находится в
находится в
![]() -нормальной
форме, то
-нормальной
форме, то
![]() -терм
-терм
![]() также находится в
также находится в
![]() -нормальной
форме. Таким образом, подмножество
-нормальной
форме. Таким образом, подмножество
![]() -образов
-образов
![]() -термов
с правилами
-термов
с правилами
![]() и
и
![]() -редукции
и
-редукции
и
![]() -конверсии
образуют систему, изоморфную
-конверсии
образуют систему, изоморфную
![]() -исчислению,
со всеми вытекающими отсюда следствиями.
-исчислению,
со всеми вытекающими отсюда следствиями.
Если
исключить присваивания, блоки и, без
потери выразительности, рекурсивные
процедуры, то даже без расширенного
набора констант (правила 19,20) получим
чисто функциональный язык (в [
] он был назван исчислением
функциональных абстракций – ИФА), по
своим возможностям очень близкий к
![]() -исчислению.
Система правил редукции и конверсии
для ИФА будет выглядеть так (с рекурсивными
процедурами):
-исчислению.
Система правил редукции и конверсии
для ИФА будет выглядеть так (с рекурсивными
процедурами):
-


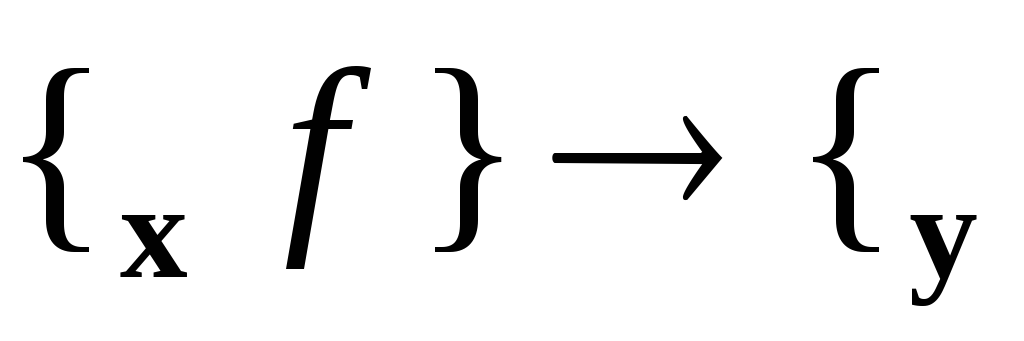 [
[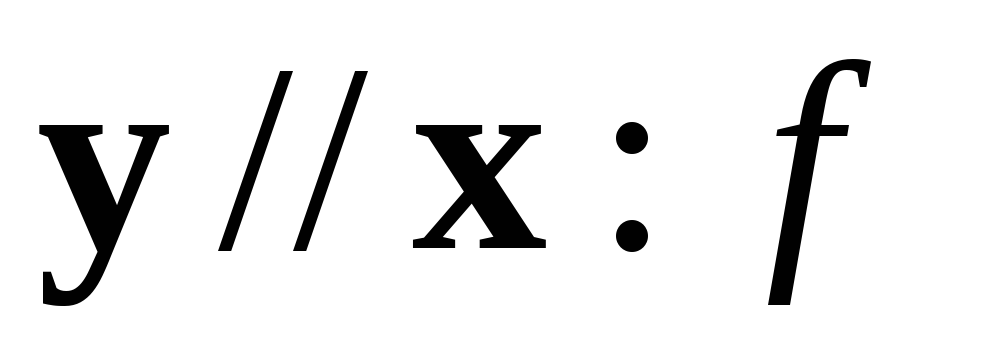 ]
] ;
; -
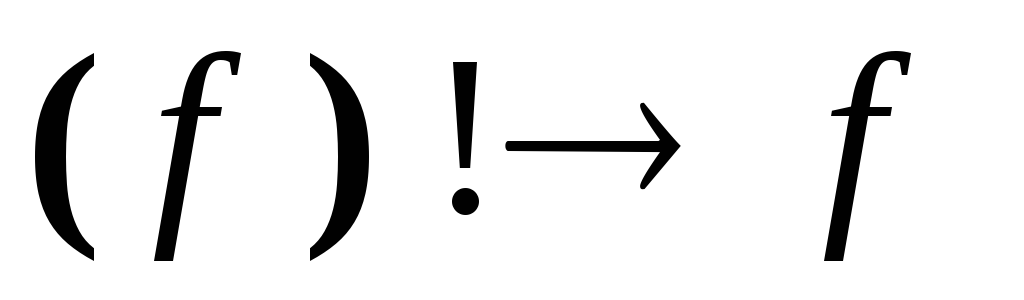 ;
; -
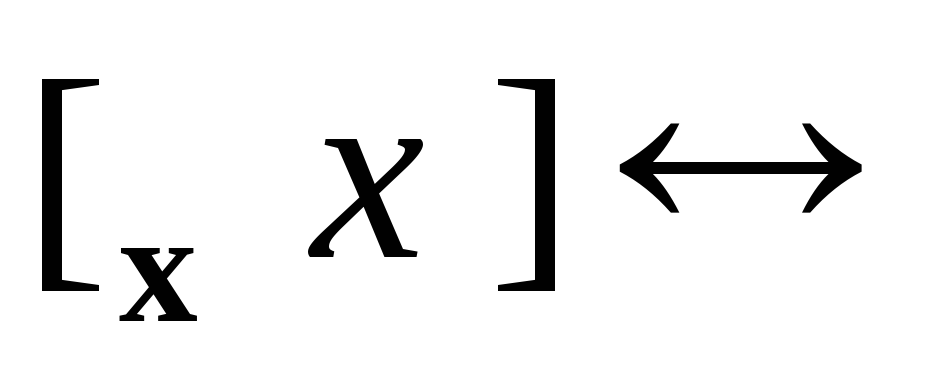 ;
; -
 ;
; -


 ;
; -

 ;
; -


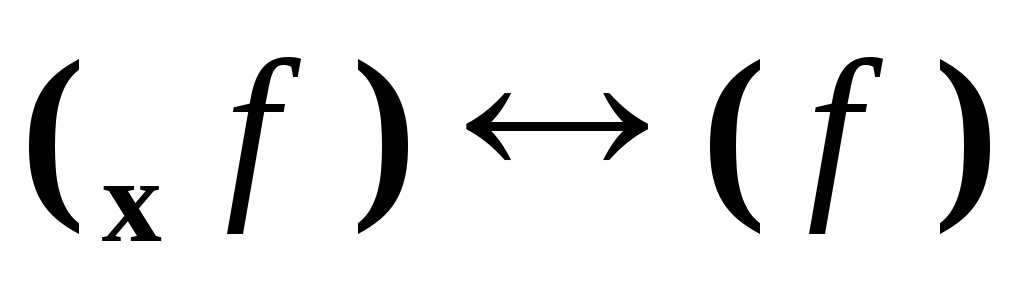
или так (без рекурсивных процедур):
-


 [
[ ]
] ;
; -

-
 ;
; -

-


 ;
; -

 .
.
Определим
правила конвертирования
![]() -термов
в ИФА:
-термов
в ИФА:
-
 ;
; -
 ;
; -
 .
.
Для
правила
![]() -редукции
получим диаграмму
-редукции
получим диаграмму

