4. Денотационная семантика.

Денотационная семантика FALGOLа определяется в форме некоторых отношений на множестве термов – содержательного включения, содержательной эквивалентности и содержательной несравнимости. Приведенные ниже определения этих отношений не являются конструктивными; и, как станет понятным далее, проблема содержательной эквивалентности термов вообще является алгоритмически неразрешимой.

Определение 3.Терм содержательно включает терм (обозначается ), если

.

Определение 4.Терм содержательно эквивалентен терму (обозначается ), если .

Определение 5.Терм содержательно не сравним с термом (обозначается ), если

.

Заметим, что операции конструирования термов являются монотонными относительно отношений содержательного включения и содержательной эквивалентности:

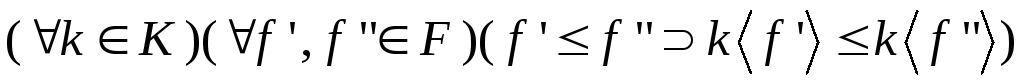и

.

4. Трансформационная семантика.

Трансформационная семантика FALGOLа задается множеством правил редукции и конверсии, сохраняющих содержательную эквивалентность термов. Пусть , обозначают либо вызовы значений переменных, либо процедуры, , , – термы.

Правила редукции-конверсии:

1. ;

2. ;

3. ;

4. ;

5. ;

6. , где ;

7. ;

8. , где ;

9. ;

9. ;

10. , где , если ;

11. ;

12. , где , если ;

13.  ;

14.  ;

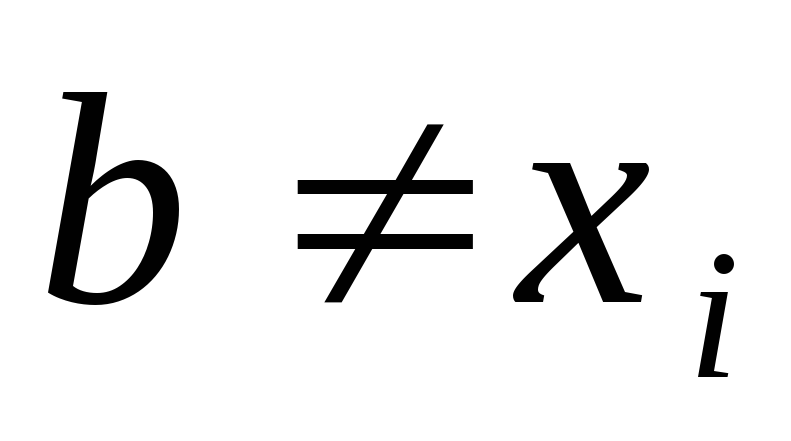
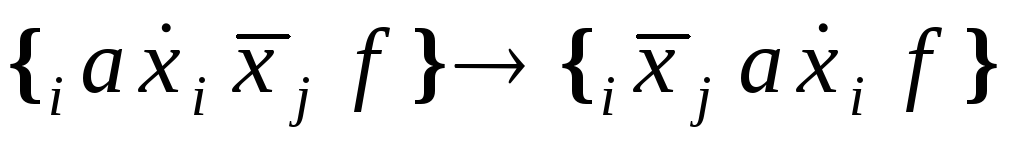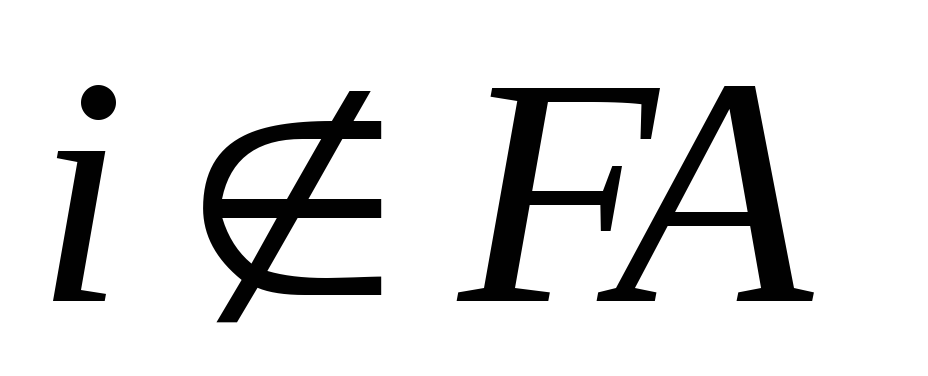
15. ; где - «неопределенное» инициальное значение, выполнение терма как программы на FALGOL-машине никогда не завершается;

16. Сборка «мусора». Пусть 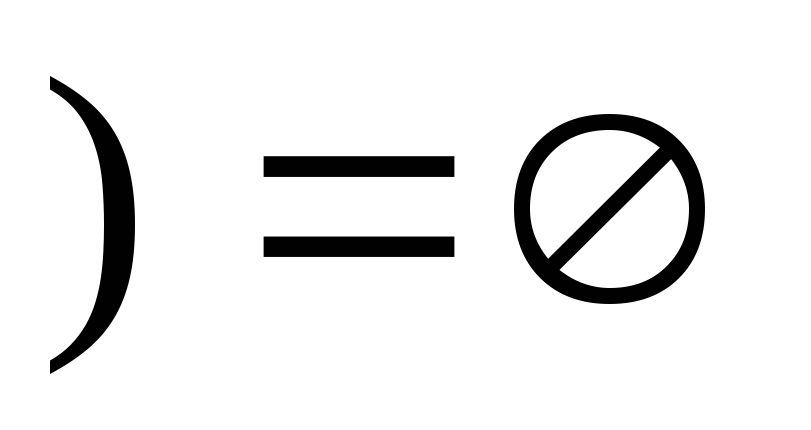. Тогда



,

где – результат подстановки вместо в .

Правила вывода.

П1. .

П2.  для всех .

4. Язык со статическим связыванием.

Язык Falgol со статическим связыванием переменных фактически представляет собой подмножество термов языка FALGOL, из числа элементов которого исключаются символы связывания переменных, а в качестве новых, вводимых по определению, элементов в языке Falgol используются введенные выше по определению конструкции:

• – «распроцедуривание»;

• – «блок» с блочной переменной и «телом» ;

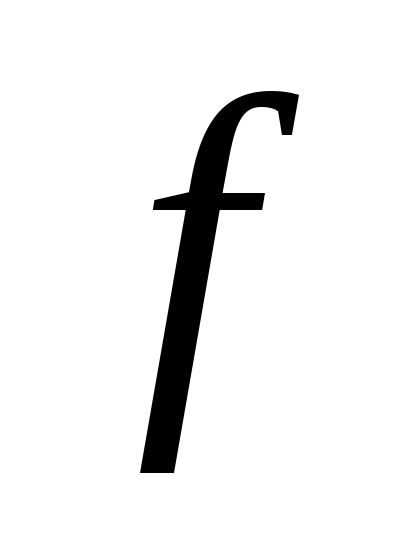• – «функция» с параметром и «телом» ;

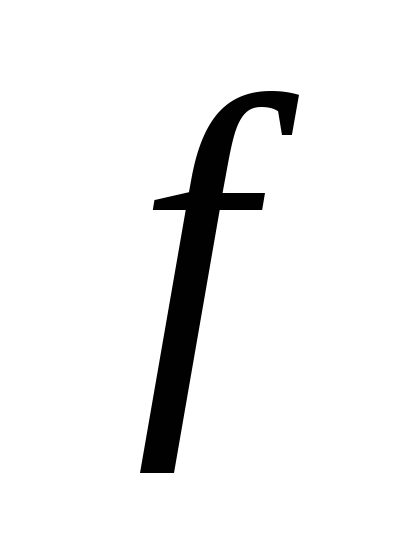• – «рекурсивная процедура» с переменной рекурсии и «телом» ;

• – «неопределенное» инициальное значение .

Множество свободно используемых переменных терма определяется теперь непосредственно так:

 ; ; ;

;.

Аналогично определяется и множество свободных изменяемых переменных терма :

 ; ; ; ;

; ; .

Все правила сохраняются в той же формулировке, за исключением правила 6:

6. .

Вводятся новые правила:

17. Для всех атомарных констант из расширенного набора (– арность константы ) полагаем, что 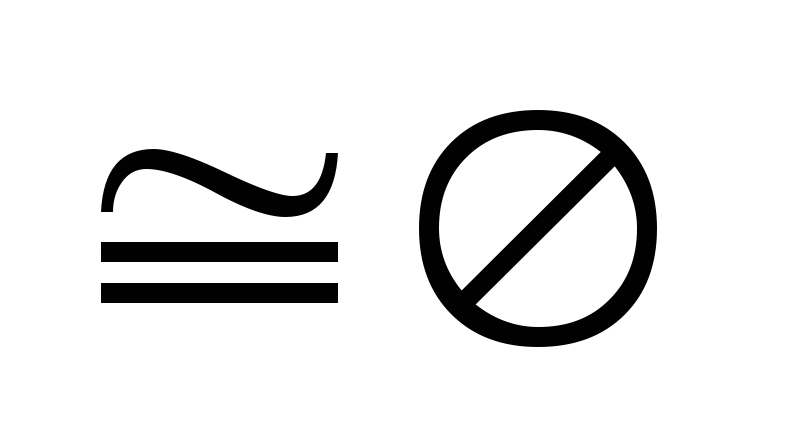 и для всех нульарных констант и (то есть все нульарные константы попарно не эквивалентны). Для атомарных констант из расширенного набора могут вводиться произвольные правила следующего вида c различными левыми частями:

,

где и , и для всех , а – произвольный замкнутый терм ();

18. для всех и ;

19. для всех и .

Согласно аксиомам и некоторым выводимым конверсиям, семантически базовой конструкцией следовало бы считать блок с некоторым множеством операторных переменных:

, где , , а при будем считать, что . В этом случае получим:

.

Введем обобщенный оператор присваивания как частичное отображение множества переменных в множество объектных термов, т.е. в объединение множества вызовов значений переменных и множества термов-процедур. Для изображения обобщенных операторов присваивания будем использовать следующую нотацию: , где .