4.3.Төрт бұрышты потенциалды бөгет. Түнелдік эффект
Тік
бұрышты потенциалды тосқауыл деген
түсінік енгізейік. Ол үшін екі электронның
өзара әсерлесу потенциалдық энергиясының
диаграммасын қарастыпайық. Ядролық
күштің әсері болатын қашықтықтан алшақ
қашықтықтарда (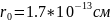
)
ядролық күш әсер ететін аймақтың радиусы
Кулондық әсер яғни тебілу күші әсер
етеді.
Диаграммадан
r>
аралықта Кулондық тебілу күші әсер
ететін аймақ екендігі көрінеді. Ал
r>
аймақта
ядролық күшті әсерлесу болатынын
көрсетеді. ( бұл ядроның ішіндегі
протондар мен нейтрондарды ұстап тұратын
күш, тағыда тебілу күшімен алмасады,
бірақ күш күшті әсерлесуге жатады.
Кулондық әсерлесу емес. Диаграммадағы
тік бұрышты потенциалдық тосқауылдың
биіктігі шамамаен 200 Мэв- тең. Ал оң
жақтағы тосқауылдың биіктігі шамамен
25 М.эв .
,
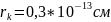r>
Қашықтық протонды жақындата алса
ядролық синтез реакциясы жүзеге асып
Дитери атомының реакциясы түзіледі.
Бірақ ондай қашықтыққа жеткізу үшін
бөлшектер потенциалдық тоссқауылдың
кедергісіне ұшырайды.
.
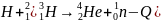Бөлшектер бұл тосқауылды жеңу үшін
оларды өте үлкен температурады қыздыру
қажет. Мұндай температураға жеткізу
оңай емес. Оданда қиынрақ ондай
температурадағы плазманы ұстап тұратын
зат табу оданда қиын. Сондықтан кванттық
механикада микробөлшек энергиясы аз
болсада тосқауылдан өтіп кету ықтималдылығы
барма деген сұраққа жауапіздейді. Осы
есепті қарастырайық: бөлшектер ағыны
биіктігі h- болатын ох осінің бойында
орналасқан потенциалдық тосқауылға
қарай ох бағытында қозғалсын. Мұндағы
а- тосқауылға түскен бөлшектер ағыны,
В- тосқауылдан шағылған бөлшектер ағыны
, С- тосқауылдан өтіп кеткен бөлшектер
ағыны. Осы есепті шығарайық . ең қарапайым
жағдай микробөлшектің тік бұрышты
тосқауылдан өтуін қарастырайық. Ол
мынасуретте бейнеленген. Тосқауылдың
потенцциалдық энергиясының өрнегі мына
түрде жазылады. U(x)=
,
Әр аймақ үшін Шредингер теңдеуін
жазайық
,
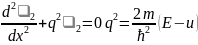
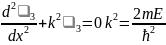Шредингер теңдеуінің шешімі болу
үшін функциясының қасиетіне сәйкес
үздіксіз болуы шарт. Ол үшін келесі
шарт орындалуы тиіс.
,
,
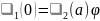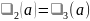
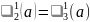Әр аймақ үшін (13)-ші теңдеулер жүйесінің
шеімін жазайық,.
Мұндағы
А,В,С,Д,F және G (14)-ші шарттарды
қанағаттандыратындай тұрақтылықтар
болуы керек. I және II Аймақтарда
микробөлшек еркін еркін бөлшек ретінде
қозғалады. Олай болса
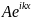өрнегі
ох бағытында қозғалып келіп тосқауылға
түскен бөлімді сипатталады. Ал
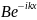потенциалдық
тосқауылдан кері шағылған бөлшекті
сипаттаса қозғалатын
тосқауылға
сол жағынан келген бөлшектерді сипаттайды.
Бірақ біздің есебімізде бөлшектер
тосқауыл тек оң жағынан келіп түседі.
Сондықтан G=0. Тосқауылға түскен шағылған
және өтіп кеткен бөлшектің мөлшерін
өзара салыстыру үшін түскен шағылған
және өтіп кеткен бөлшектер үшін
ықтималдылықтар ағынынң тығыздық
өрнегін жазайық. 2.3- лекцияның 23- ші
өрнегіне сәйкес .
.
.
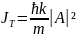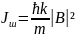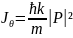(16)- шы өрнекті пайдаланып бөлшектің
тосқауылдан өту коэффициентімен шағылу
коэффициентін анықтайық. Өту коэффициентін
–әрпімен белгілейік. P =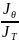
=
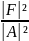, Шағылу коэффициентін – деп белгілейік.
Ол
P
=
=
,
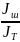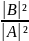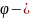Толқындық
функцияның үзіліссіздік қасиетіне
байланысты
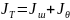(19)
(19)- өрнекке сәйкес және коэффициентінің байланысын жазуға болады. P+R = 1 (20)
(17)-(18)-(19)-(20)
өрнектерді пайдаланып шекаралық
шарттарды (14) пайдаланып А,В,Д,С,Ғ,
коэффициенттерін есептейік.
,
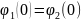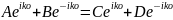
A+B=C+D
(21),
,
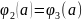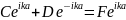(22)
(15)
–ші теңдеулер жүйесінен х-бойынша
туынды алсақ 1-ші мен 2-шіні және 2-ші мен
3-шіні бір-біріне теңестірейік.
K(A-B)=q(C-D) (23), Q(
(24),
(21), (22), (23), (24) теңдеулерді былайша
біріктірейік. А+В=С+Д, А-В=
,
,
,
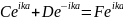(25)-ші теңдеулердің 1-ші және 2-ші теңдеулерін
бір – біріне қоссақ, содан
2A
= C + D+
,
A=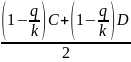
;
3-ші
мен 4-ші теңдеулерді бір-біріне қоссақ
,С-ны табамыз. 2С*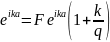
C
=
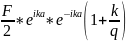(27),
3-пен 4-ші бір-бірінен алып, содан Д-ны
тапсақ
2D*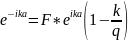
(28), D=
,
(27)-(28) теңдігі С және Д коэффициентін
(26)-шы теңдеуге қойсақ
A=
;
Осы
қатынастың көмегімен
–ны
тапсақ;,
;
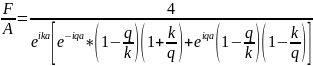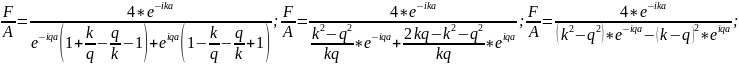
Микробөлшектің тосқауылдан өту коэффициентін (P) –ны алайық;
P=
=
;
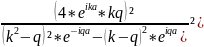Ал шағылу коэффициеті
R
P+R=1,
R=1-P=1-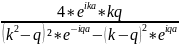
(32),
Микробөлшектің энергиясы тосқауылдың
энергиясынан артық болады. (32)-ші өрнектен
көрініп тұрғандай классикалық механика
заңына бағынбайтын құбылыс, яғни
энергиясы тосқауылдың потенциалдық
энергиясынан артық болса да, тосқауылдан
кері қарай шағылатын микробөлшектің
де болатындығын көреміз. Өйткені шағылу
коэффициенті (R) 0-ге тең емес, яғни
тосқауылдың потенциалдық энергиясынан
артық энергиясы бола тұра тосқауылдан
шағылатын бөлшектің болу ықтималдылығы
0-ге тең емес. Енді микробөлшектің
энергиясы тосқауылдың потенциалдық
энергиясынан кем болған жағдайды
қарастырайық. E<U Ол үшін q –жорамал
шаманы q=if деп белгілейік. Мұндағы f =
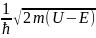(33)
Осыны
ескеріп ,
Сонда өту коэффициенті (35)-ші өрнектен
микробөлшектің энергиясы тосқауылдың
потенциалдық энергиясынан аз болса да,
тосқауылдан өтіп кету мүмкіндігі бар
бөлшектің де болатындығын көреміз. Бұл
құбылысты классикалық механика заңы
түсіндіре алмайды. Бқл құбылыс туннельдік
эффект деп аталадыӨйткені бөлшек
тосқауылдың үстінен асып өте алмайды.
Өйткені энергиясы өте аз олай болса ол
тек тосқауылдан туннель қазып өте
алады.Туннельдік эффект бұл кванттық
құбылыс. Яғни микробөлшектің толқындық
қасиетінің болатындығын дәлелдейді.
Осы құбылыстың нәтижесінде көптеген
физикалық қасиеттер атап айтқанда
ядролардың бөлінуі мен ыдырауы
термоэлектрлік эмиссия т.б құбылыстарды
түсіндіруге мүмкіндік береді.