3.5. Энергиямен импульс үшін анықталмағандықтар арақатынасы.

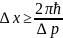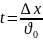Бөлшек стационар емес күйде болсын. Бұл жағдайда бөлшектің нақты анықталған энергиясы болмайды. Анықталмағандықтардың арақатынасына сәйкес: (6) (7) 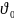- фазалық жылдамдығы . Стационар емес жағдайда стационар еместіктің өлшемі 7-ші өрнекпен анықталады. - толқындық пакеттің центрінің жылдамдығы, ал мына өрнекпен анықталады. Олай болса, 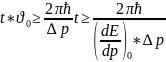(8) Мұндағы, 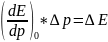(9) деп белгілейік. 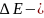бөлшектің энергиясының анықталмағандығы деп аталады. 9-ші өрнекті 8-ге қойсақ 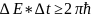(10) 10-ші өрнек энегия мен уақыт үшін анықталмағандықтар арақатынасы деп аталады. 10-ші өрнек пен 5-ші өрнек бір-біріне сәйкес келгенмен 10-ші өрнектің физикалық мағынасы басқаша. 10-ші өрнектің физикалық мағынасы: 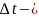уақыт аралығында бөлшектің энергиясын дәл анықтау мүмкін емес тек ықтималдылықпен анықтау мүмкін.

4.1.Финитті және инфинитті қозғалыстар.

Микробөлшектің бір өлшемді қозғалысын қарастырайық , Бұл жағдайда микробөлшектің потенциал энергиясы бір координатаға (x)-ке тәуелді болады және микробөлшектің күйін сипаттайтын осы айналымға тәуелді болады . Мұндай микробөлшектің күйін анықтау үшін Шреденгердің стационар бір өлшемді теңдеуі қолданылады . 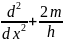E-U(x)=0 (1), -функциясы бір мәнді үздіксіз модуль бойынша шектелген болған жағдайда ғана физикалық мағынасы болады .Шексіздікке микробөлшектің потенциал энергиясы U(x)=.Бұл кезде толқындық функция 0-ге тең болады.Mысалы : (1*), Потенциал энергия шексіз оң мәнге ие болғанда микробөлшек шексіз үлкен тебілу күшіне ие болады. 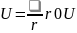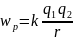 , Екі аттас зарядтарды бір-біріне жақындатсақ олай болса микробөлшектің мұндай нүктеге ( жету ықтималдылығы 0-ге тең. 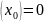, Осы жағдайды сипаттайтын энергияның координатаға тәуелділігі графигін сызайық. Х=0 нүктеде U(x) өте үлкен мәнге ие. Сондықтан микробөлшектің ол нүктеге жету ықтималдылығы 0-ге тең . x  микробөлшектің күйі толық энергияның таңбасына тәуелді болады. Бұл кезде U(x)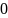 .Бұл жағдайда бірінші теңдеу мына түрге енеді 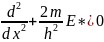(2), 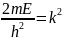, 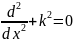( 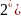. ( -өрнек тәуелсіз екі сызықтық шешімге ие болады. , 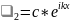(3), Егер Е0 болса тек 3- ші теңдеулер жүйесінің бірінші теңдеудің ғана мағынасы болады. Өйткені 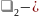шексіздікте 0-ге тең Ал . x  нүктесінде 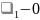.Бұл микробөлшектің координата басынан шекті арақашықтықта ғана болу ықтималдылығы ьар екендігін көрсетеді. Мұндай қозғалыс финтті қозғалыс деп аталады Е0 болған жағдайда энергияның бір мәніне функцияның екі әртүрлі шешімі сәйкес келеді Бұл 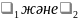шешімінде микробөлшектің координата басынан шексіздікке дейін қозғалысын, және шексіздіктен координата басына дейінгі қозғалыстарын сипаттайды. Микробөлшектің мұндай қозғалысы инфинитті қозғалыс деп аталады. ( финитті екі жағынан шектелген қозғалыс, инфинитті тек бір жағынан шектелген қозғалыс). Сонымен микробөлшектің қозғалысы финитті болады. толық энергия нөлден кіші болғанда ал инфитті қозғалыс 0 ден үлкен болғанда.

4.2.Бір өлшемді потенциалдық шұңқырдағы бөлшек.

Микробөлшетің кеңестіктің белгілі бір шекті аймағында ұстап тұра алатын потенциалдық өріс шексіз потенциалдық шұңқыр ретінде қарастырылады.Бір өлшемді қозғалыс жағдайында о<x<a аралығында потенциялдық энергия U(x)=0, ал x≤0 аралықта, х=≥а болады потенциялдық энергия U(x)∞

Бұл шарттар микробөлшек ОХ бойындағы 0 мен а нүктесінің аралығында ғана бола алатындығын , ал аралықты микробөлшектің тастап кете алатынын көрсетеді. Себебі бұл аймақтың шекарасына микробөлшектің кері қарай қайтарушы күшінің мәні шексіз үлкен болады.

Микробөлшек бұл аралықта тастап кету үшін микробөлшектің кинетикалық энергиясы үлкен мәнге ие болу керек. Шындығында потенциалдық шұңқыр ішкі микробөлшектің кинетикалық энергиясы белгілі бір мәннен аса алмайды.(шекті мәнге ие)

(1)теңдеуі потенциалдық шұңқыр ішіндегі бөлшек үшін =0

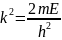
Микробөлшектің шекарадан шығып кету ықтималдылығы 0-ге тең болады

(0)=0 (а)=0 (4)

Бұл жағдайдағы жалпы шешім

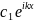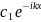= + (5)

Соңғы өрнектен х=0 жағдайын қарастырып (4)-ші шартты пайдаланып (5)-ші теңдеудегі тұрақтысын табуға болады . Яғни

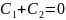
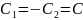
=Сsinkx (6)

Мұндағы к=5 шартты қанағаттандыру үшін мына өрнек анықталады

(8)

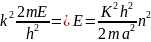
(9)

(9) Өрнектен энергия квантталатын шама екендігі шығады . Оның физикалық мағынасын бөлшектер ерекше стоционар күйде болады. Әр стоционар күйдің өзіне сәйес энергиясы болады.

(8)өрнектегі 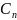коэфициентінің мәнін анықтау үшін нормалау шартын ескеріп жазайық.

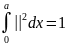(10)

Осы интегралды шешсек

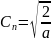(11)

Бөлшектің х координатасы үшін ықтималдылық тығыздығының таралуы келесі диаграммада көрсетіледі

Сондықтан кванттық (n) санының артуымен яғни энергияның артуымен микробөлшектің қасиеттері классикалық бөлшекке жақындай түседі.