2.3. Ықтималдық ағынының тығыздығы.

Микробөлшектің қозғалысы кеңістікте 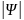² ықтималдылық тығыздығы бойынша таралуымен сәйкес келеді. Яғни бөлшектің кеңістіктегі қозғалысы ықтималдылықтар ағынының тығыздығы деп аталатын арнайы шаманың көмегімен сипатталады. Бұл шама кванттық механиканың негізгі теңдеуіне сүйене отырып алынады: 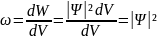, 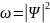(18) Бұл шаманың уақытқа тәуелді өзгеруін анықтайық: 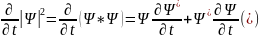Шредингер теңдеуінен:

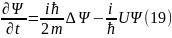
Дәл осы сияқты комплексті түйіндеудің операторын жазсақ: 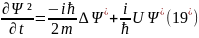, (19) және ( ) өрнекті (*) өрнекке апарып қойсақ:

Сонда:

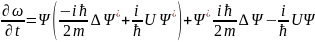
Бұдан: , (20) теңдеу былай жазылады: 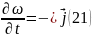, Мұндағы: 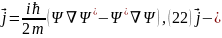ықшамдықтар ағыны тығыздығының векторы.

2.4.Бөлшектер санының сақталу заңы. Бөлшектердің еркін қозғалысының толқындық функциясы.

Ықтималдықтардың сақталуын бөлшектер санының сақталуымен түсіндіруге болады, ол үшін кеңістікте бір біріне тәуелсіз бірдей кванттық күйде болатын бірдей N микробөлшектер бар деп қарастырайық. Бұл бөлшектердің барлығы бір ғана толқындық функциямен сипатталсын. Егер N>>1 болса онда кеңістіктің әрбір нүктесіндегі бөлшектер тығыздығыа тең болады. Ал - Интегралы кеңістіктің, V көлеміндегі бөлшектер санын анықтайды. Олай болса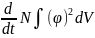 туындысы V көлемдегі бөлшектер санының бірлік уақыт ішіндегі өзгеруін сипаттайды.

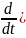, (23) Сонымен (23*), (23*) өрнек кванттық механикадағы бөлшектер санының сақталу заңы деп аталады. ОЛ былайша тұжырымдалады. Кеңістіктің қандайда бір V көлеміндегі бөлшектер ес түссіз жоғалмайды немесе жоқтан бар болмайды, ол тек басқа аймақтан енуі мүмкін немесе басқа аймаққа шығуы мүмкін.

2.5

Шредингер теңдеуін еркін бөлшектер үшін қарастырайық. Микробөлшектер әлемінде сыртқы әлем болмаған жағдайдағы потенциалдық энергиясы (U=0)-ге тең болған жағдайдағы бөлшек еркін бөлшек деп қарастырылады. Бұл стационар өрістің бір жағдайы яғни бөлшектің энергиясы сақталады. Сондықтан Шредингердің стационар өріс үшін (14)-ші теңдеуге көшуге болады. Еркін бөлшек үшін бұл теңдеуді мына түрде жазады:

Мұндағы, ,

*

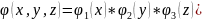
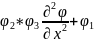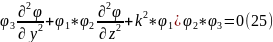
(25)-ші теңдеуді

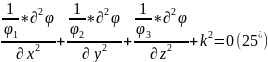
(26)-ші теңдеулер жүйесінен көрініп тұрғандай бір типті 3 теңдеу алдық.

Сондықтан, тек бір теңдеуді шешу жеткілікті.

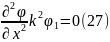. Бұл теңдеу 2-ші реттік дифференциалдық теңдеу.

Бұл теңдеу математикада толық шешілген теңдеу болып табылады және оның дербестік шешімі мына түрде жазылады:

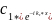
Яғни, жалпы жағдайда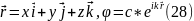

уақытқа тәуелсіз болатын тұрақты шаманы енгізейік, ондай шамаға импульс векторын жатқызуға болады.

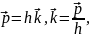сонда

Егер уақытқа тәуелді болған жағдайда бұл теңдеуді былайша жазады.

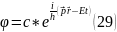
Бұл теңдеу жазық монохроматтың теңдеуі болып табылады және Дебройль теңдеуімен сәйкес келеді.

3.1. Импульстің анықталмаған мәніндегі күйі.

(2.29) теңдеуі еркін қозғалатын бөлшектің күйін сипаттайтын толқындық функция болып табылады. Бұл теңдеуде координаталардың нақты мәндері жоқ.

Импульстің оның координатаға проекциясының,энергияның импульс моментінің т.б. физикалық шамалардың сәйкес келетін еркін бөлшектерінің күйлері болуы мүмкін.

2лекциядағы (2.29)теңдеу 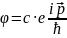. Толқындық функциядағы импульстің берілген мәніне сәйкес келетін күйді сипаттайтын теңдеу. Прцессті толық сипаттау үшін: 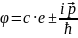^·x (3.1)

Мұндағы (-) ох осьіне кері бағытта тараған толқынға сәйкес келеді.

Суперпозиция принципіне сәйкес келетін бөлшектің қандай да бір нақты күйін сипаттайтын теңдеу былайша жазылады:

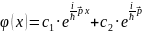₂x (3.2) Алынған өрнектен жалпы мынадай қорытынды жасауға болады: Микронбөлшектің нақты күйін сипаттайтын толқындық функцияда кейбір физикалық шамалар нақты мәнге ие болмайды.