
- •Кванттық механика лекция
- •1.1.Атомның тұрақтылығының және сәуле шығаруының мәселелері. Жарықтың корпускулалық қасиеттерінің байқалуы.
- •1.2.Комптон эффектісі
- •1.3 Атом энергиясының деңгейлерінің дискреттілігі. Бордың жартылай классикалық теориясы
- •1.4. Де Бройл гипотезасы. Корпускулалық толқындық дуализм
- •2.1 Күй функциясы. Күйлердің суперпазитция принципі.
- •2.2.Шредингер теңдеуінің түрі және оның шешімінің жалпы қасиеттері. Стационар күйлер.
- •2.3. Ықтималдық ағынының тығыздығы.
- •2.4.Бөлшектер санының сақталу заңы. Бөлшектердің еркін қозғалысының толқындық функциясы.
- •3.1. Импульстің анықталмаған мәніндегі күйі.
- •3.2.Толқындық пакет.
- •3.3.Гейзенбергтің анықталмағандықтар арақатынасы.
- •3.4.Анықталмағандықтар арақатынасы және физикалық шамаларды өлшеу. Энергия мен импульс үшін анықталмағандықтар арақатнасы.
- •3.5. Энергиямен импульс үшін анықталмағандықтар арақатынасы.
- •4.1.Финитті және инфинитті қозғалыстар.
- •4.2.Бір өлшемді потенциалдық шұңқырдағы бөлшек.
- •4.3.Төрт бұрышты потенциалды бөгет. Түнелдік эффект
- •5.1 Есептің қойылуы. Гармоникалық осциллятор үшін Шредингер теңдеуін шешу.
- •5.2. Гармоникалық осциллятор есебінің шешімін талдау.
- •5.3.Квазиклассикалық жуықтаулар.
- •6.1.Функцияны жалпыланған қатарға жүктеу. Фурье интегралы.
- •6.2.Сызықты операторлар.
- •6.3.Меншікті функциялар және операторлардың меншікті мәндері.
- •6.4.Өздік түйіндес операторлар.
- •8.1 Физикалық шамалардың орташа мәндерінің уақыт өтуімен өзгеруі, Эренфест теңдеуі
- •9.3 Орталық симметриялық өрістегі бөлшектің қозғалысы.
2.2.Шредингер теңдеуінің түрі және оның шешімінің жалпы қасиеттері. Стационар күйлер.
Классикалық
механикадағы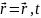 макро
бөлшектердің (материалдық нүктенің)
кез-келген уақыт мезетіндегі механикалық
күйін сипаттайтын теңдеу болып табылады.
Ал кванттық механикада (7)
теғдеуге пара-пар теңдеу, яғни микро
бөлшектің күйңн сипаттайтын толқындық
функция түрінде жазылады.
макро
бөлшектердің (материалдық нүктенің)
кез-келген уақыт мезетіндегі механикалық
күйін сипаттайтын теңдеу болып табылады.
Ал кванттық механикада (7)
теғдеуге пара-пар теңдеу, яғни микро
бөлшектің күйңн сипаттайтын толқындық
функция түрінде жазылады. ,t)
(8) Классикалық
механикадағы негізгі мәселе материалдық
нүктенің кез-келген уақыт мезетіндегі
орны мен жылдамдығы анықтау болатын.
Бұл мәселе классикалық механиканың
негізгі теңдеуі-Ньютонның екінші заңымен
іске асады.Кванттық механикада берілген
уақыт мезетіндегі күштік өрістегі орнын
анықтау. Кванттық механикадағы негізгі
теңдеу-Шредингер теңдеуінің көмегімен
іске асады. Щредингер теңдеуінің жалпы
түрі мына түрде жазылады:
,t)
(8) Классикалық
механикадағы негізгі мәселе материалдық
нүктенің кез-келген уақыт мезетіндегі
орны мен жылдамдығы анықтау болатын.
Бұл мәселе классикалық механиканың
негізгі теңдеуі-Ньютонның екінші заңымен
іске асады.Кванттық механикада берілген
уақыт мезетіндегі күштік өрістегі орнын
анықтау. Кванттық механикадағы негізгі
теңдеу-Шредингер теңдеуінің көмегімен
іске асады. Щредингер теңдеуінің жалпы
түрі мына түрде жазылады:
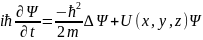 (9)Бұл
дербес туындысы бар дифференциялдық
теңдеу, Мұндағы:
і-жорамал
бірлік,
(9)Бұл
дербес туындысы бар дифференциялдық
теңдеу, Мұндағы:
і-жорамал
бірлік,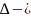 Лаплас
операторы,m
Лаплас
операторы,m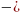 бөлшек
массасы,
бөлшек
массасы,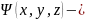 толқындық
функция,
толқындық
функция,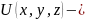 бөлшектің
сыртқы күштікөрістегі потенциялдық
энергия. Нақты есептерде Потенциялдық
энергияның координатасымен уақытқа
тәуелділігінің бірнеше жағдайы болуы
мүмкін.
функциясы
берілген жағдайда (9)
Щредингер теңдеулерінің жалпы шешімін
табуға болады. Жалпы шешім қандай да
бір координатамен уақытқа тәуелді еркін
функциядан тұрады. Бұл функцияны бастапқы
және шекаралық шарттардың көмегімен
анықтайды. Бастапқыт шарт (t=0) кезде
бөлшектің
сыртқы күштікөрістегі потенциялдық
энергия. Нақты есептерде Потенциялдық
энергияның координатасымен уақытқа
тәуелділігінің бірнеше жағдайы болуы
мүмкін.
функциясы
берілген жағдайда (9)
Щредингер теңдеулерінің жалпы шешімін
табуға болады. Жалпы шешім қандай да
бір координатамен уақытқа тәуелді еркін
функциядан тұрады. Бұл функцияны бастапқы
және шекаралық шарттардың көмегімен
анықтайды. Бастапқыт шарт (t=0) кезде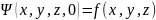 (10)
. Шекаралық
шартты анықтауда толқындық функцияның
мәндеріне қандай да бір кеңістіктің
шекарасындағы немесе шексіздіктегі
мәндерін береді. Бастапқы және шекаралық
шарттардың және нормалау шартының жиыны
толқындық функцияның, яғни Щредингер
теңдеуінің дербес шешімдерін береді.
Ψ-функциясы анықталған жағдайда
кез-келген уақыт мезетіндегі күйін
сипаттауға болады. Бұл кванттық
механикадағы себептілік принціпінің
негізін қалайды. Ол былайша тұжырымдалады:
Ψ-функцияның бір мәнді динамикалық
заңдылығы болған жағдайда микробөлшектің
статистикалық заңдылығын анықтауға
болады. Сонымен кванттық механиканыңнегізгі
теңдеуі сызықтың біртекті және дербес
туындылардан тұратын дифференциялдық
теңдеу болып табылады. Стационар
потенциялдық өрістегі, яғни потенциялдық
энергиясы уақытқа тәуелді болмайтын
өрістегі бөлшектің қозғалысын қарастыру
теориялық және практикалық маңызға ие.
Ол үшін Щредингер теңдеуін 2 тәуелсіз
функцияға жіктейді.
(10)
. Шекаралық
шартты анықтауда толқындық функцияның
мәндеріне қандай да бір кеңістіктің
шекарасындағы немесе шексіздіктегі
мәндерін береді. Бастапқы және шекаралық
шарттардың және нормалау шартының жиыны
толқындық функцияның, яғни Щредингер
теңдеуінің дербес шешімдерін береді.
Ψ-функциясы анықталған жағдайда
кез-келген уақыт мезетіндегі күйін
сипаттауға болады. Бұл кванттық
механикадағы себептілік принціпінің
негізін қалайды. Ол былайша тұжырымдалады:
Ψ-функцияның бір мәнді динамикалық
заңдылығы болған жағдайда микробөлшектің
статистикалық заңдылығын анықтауға
болады. Сонымен кванттық механиканыңнегізгі
теңдеуі сызықтың біртекті және дербес
туындылардан тұратын дифференциялдық
теңдеу болып табылады. Стационар
потенциялдық өрістегі, яғни потенциялдық
энергиясы уақытқа тәуелді болмайтын
өрістегі бөлшектің қозғалысын қарастыру
теориялық және практикалық маңызға ие.
Ол үшін Щредингер теңдеуін 2 тәуелсіз
функцияға жіктейді. (10)Осы
өрнекті Щредингер теңдеуіне қояиық.
(10)Осы
өрнекті Щредингер теңдеуіне қояиық.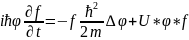 (11)
,
(11)
,
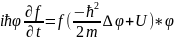 (12)
(12)
(12)
теңдеудің екі жағын да
 ке
бөлейік
ке
бөлейік
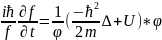 (12*)(12*)-өрнектің
сол жағымен оң жағы әр түрлі айнымалыларға
тәуелді функция. Бұл теңдеудің сол
жағындағы
(12*)(12*)-өрнектің
сол жағымен оң жағы әр түрлі айнымалыларға
тәуелді функция. Бұл теңдеудің сол
жағындағы
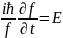 (13*)
,
(13*)
,
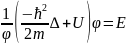 (13**)
Сонымен толқындық функцияның уақытқа
(13) және координатаға (14) тәуелді екі
өз-ара тәуелсіз 2 теңдеулерге бөлдік.
(13)-теңдеудің жалпы шешімі математикадан
белгілі.
(13**)
Сонымен толқындық функцияның уақытқа
(13) және координатаға (14) тәуелді екі
өз-ара тәуелсіз 2 теңдеулерге бөлдік.
(13)-теңдеудің жалпы шешімі математикадан
белгілі.
 (14)
. Бұл теңдеу Щредингердің стационар
теңдеуі деп аталады. Әдетте оны мына
түрде жазады:
(14)
. Бұл теңдеу Щредингердің стационар
теңдеуі деп аталады. Әдетте оны мына
түрде жазады:
.Әдетте
оны мына түрде жазады: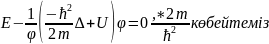
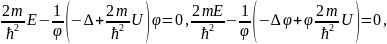
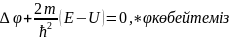
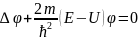 (16)
(16)
Е-микробөлшектің толық механикалық энергиясы
Ол уақытқа тәуелді болмайды. Яғни тұрақты шама. Энергиясы белгілі 1 мәнге ие болатын бөлшектің күйі, стационар күй деп аталады.
(16) теңдеудің жалпы шешімі толқындық функция ретінде былайша жазылады:
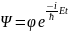 (17)
(17)
