1.4. Де Бройл гипотезасы. Корпускулалық толқындық дуализм

Дифракция және интерференция құбылысы жарықтың толқындық табиғатын растаса, ал фотоэффект және Комптон эффектісі жарықтың корпускулалық табиғатын дәлелдейді.Олай болса жарық корпускула- толқындық дуализмге ие.1923 жылы Де-Бройль жарық дуалистік қасиетін негізге ала отырып тек қана жарық емес,сонымен қатар еркін бөлшектерде корпускула-толқындық дуализмге ие деген болжам айтты.Бұл Де-Бройль гипотезасы деген атпен белгілі болды.Де-Бройль еркін бөлшекті монохроматты толқын ретінде қарастырып 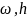сияқты шамалармен 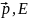сияқты механикалық шамалар арасындағы байланысты жазды. , 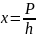(12)Де-Бройль гипотезасының дұрыс екендігін 1923 жылы Дэвиссон және Консман, кейінрек 1927 жылы Дэвиссн тәжірибесі растады.Сонымен көптеген экспериментік және теориялық мәліметтер 19 ғасырдың 2 жартысында классика механика заңдарының белгілі бір құбылыстарды түсіндіруге атап айтқанда микробөлшектер қозғаласын түсіндіруге қауқары жететіндігін көрсетті.Сонымен қатар 19ғ 2ші жартысында жарықтың корпускула-толқындық теориясы дамуына ықпал жасаған физикалық фактілер қоры жинақталды.Сондықтан аталған тығырықтан шығу жолы анықталатын физиканың жаңа бір бөлімнің пайда болуы алғышарттар дайын болды.Бұл теориялық эксперименттік алғышарттарға: Электронның ашылуы, Радиоактивтіліктің ашылуы, рентген сәуленің анықталуы, Электрон спині туралы теорияның пайда болуы, қалыптасты.Осы аталған алғышарттарды жалпылай келіп Шредингер Паули Дирак Фок және Лендау т.б ғалымдар еңбектері кванттық механика негізін қалады.

2.1 Күй функциясы. Күйлердің суперпазитция принципі.

Де Бройлдің микробөлшектердің корпускулалық толқындық табиғаты туралы гипотезасы дұрыс екендігі тәжірибемен нақтыланғаннан кейін микробөлшектер қозғалысы үшін классикалық механикадағы әдістер жарамайтындығы белгілі болды. Сондықтан микробөлшектердің кұйін сипаттайтын жаңа құрал қажет болды Ондай құрал ретінде жаңа түсінік – толқындық функция немесе күй функциясы деп аталатын Ψ пси функция енгізілді. Күй функциясы әрбір бөлшекпен байланысты болатын толқындық өрістің математикалық сипаты болып табылады. Толқындық функция микробөлшектердің параметріне тәуелді болады және микробөлшектердің физикалық шарттарына да тәуелді болады. Ψ толқындық функция микробөлшектердің механикалық күйін толқындық сипаттай алады және белгілі бір жүйеде болуының ықтималдылығымен анықталады. Айталық Ψ(x, y, z, t) берілсін онда бөлшектің t уақыт мезетінде координаттары x, y, z болатын dV элементар көлемде болу ықтималдылығы келесі өрнекпен анықталады. 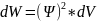(1) Бұл өрнектен: 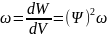- микробөлшектің орнын анықтайтын ықтималдылық тығыздығы деп аталады. Күй функциясы (Ψ) комплексті шама яғни оның модульінің квадраты. 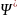(2) Мұндағы: комплекс түйіндес функция екенін көрсетеді. Комплекстік функция әрқашанда былай жазылады. 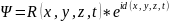(3) Мұндағы: 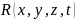функция модульі. Ал 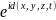—фразалық жиын деп аталады.Сонымен пси күй функциясы жеке өзінің физикалық мағынасы жоқ, бірақ оның квадраты микробөлшектің кеңістіктің қандайда бір V көлемде болу ықтималдығын береді. Бірінші бөлшекті интегралдау арқылы. (4) Ықтималдылықтың жиынтығын табуға болады, бұл күйлердің суперпазитсия принципі деп аталады. Егер (4) интегралды бүкіл кеңістік бойынша интегралдасақ. 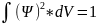(5) . (5) өрнек күй функциясының нормалау шарты деп аталады. Ψ – функция теориялық жолмен анықталғанда (5) интеграл 1-ге емес қандайда бір n деген санға тең болып қалады. Яғни Ψ функция нормаланбаған болып шығады. Сондықтан мұндай жағдайда Ψ функция нормалау үшін Ψ функция ге көбейту қажет болады. Сонымен Ψ функция микробөлшектің күйін сипаттау үшін келесідей шарттарды қанағаттандыру керек.

1. Ψ функция 1 мәнді болуы керек

2. Ψ функция үздіксіз болуы керек

3. Ψ функция квадрат – интегралдық болуы шарт.

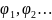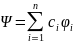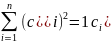Классикалық механикалық физиканың басқа бөлімдеріндегі сияқты суперпазиция принципі орындалады. Ол былайша тұжырымдалады : Берілген шарттарды қанағаттандыратын толқындық функциясы арқылы сипатталатын әртүрлі күйдегі бөлшектер берілген жағдайда келесі сызықтық комбинатциямен сипатталатын бөлшектің күйі де бола алады. (6) Бұл теңдеу Классикалық механикадағы суперпазитция принципі.Мұндағы: = комплекстік сандар. Классикалық механикадағы суперпазитция принциі былайша толығырақ айтуға болады: Берілген шарттағы бөлшектің Ψ функциясы мен сипатталатын болса яғни 6 шы өрнек орындалатын жағдайда бөлшектің ықтималдылығы 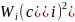күйде болу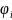ы. күйде болу ықтималдылығына тең болады. Сонымен толқындық функцияны қосу микробөлшектер әлеміндегі күйлердің суперпазитциясының ерекшелігі болып табылады, яғни толқындық функция микробөлшектердің күйін сипаттайтын математикалық құралдың негізі болып табылады.